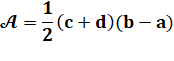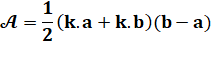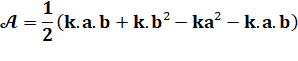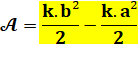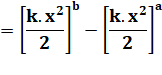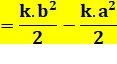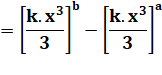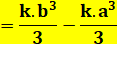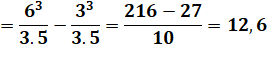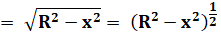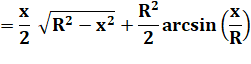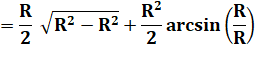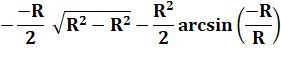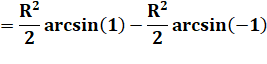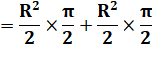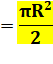|
||||||||||||||||||||||||||||||
![]()
|
Calcul par intégration ou sommes infinies Le calcul de la position
d'un centre de gravité est simple lorsque la forme géométrique présente des symétries. Les
choses deviennent plus difficiles pour les formes un peu plus complexes,
notamment comportant des arrondis. S'agissant de trouver un
point d'équilibre de la matière autour du centre de Nous faisons face alors à
des sommes, d'autant plus nombreuses que notre découpage est fin. Un passage
à la limite tendant vers une infinité de grains de matières de taille zéro
conduit à ce qui s'appelle le calcul par intégration. |
Cette page
n'est pas un cours, mais une approche, une initiation!
|
|
|||
|
Aire = demi somme des bases
multipliée par la hauteur:
|
|
||
|
En remplaçant: |
|
||
|
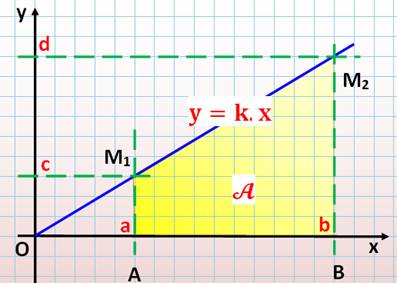
Voici une nouvelle méthode
qui sera généralisable à n'importe quelle fonction, pas seulement celle de la
droite. |
|||
|
Fonction de départ: |
y |
= k . x |
|
|
Quelle est la fonction dont
la dérivée
est celle-ci? Règle pratique de la dérivée: l'exposant devient coefficient et le nouvel exposant est l'ancien
moins un. On "retourne" cette recette pour obtenir la primitive. |
Y |
La dérivée de x² est
2x, et La primitive de x
est ½ x². = ½ k . x² |
|
|
L'aire est la différence de
cette fonction calculée entre b et a. |
|
|
|
|
|
|||
|
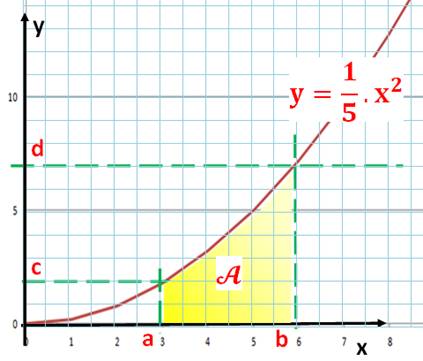
Nous sommes en présence
d'une parabole d'équation y = 0,2
x². Nous souhaitons connaître
l'aire du segment de parabole ente x = a et y = b. Une première méthode approximative
consiste à compter les petits carreaux, en faisant attention aux échelles sur
x et sur y. Ici, nous trouvons: 22
carrés pleins et 6 partiels, soit 25 carré, et en tenant compte de l'unité en
x: 12,5 unités carrées. |
|
||
|
Par la méthode de
l'intégrale |
y |
= k . x² |
|
|
Quelle est la fonction dont
la dérivée est celle-ci? |
Y |
La dérivée de x3
est 3x2, et La primitive de x2
est 1/3 x3. = 1/3 k . x3 |
|
|
L'aire est la différence de
cette fonction calculée entre b et a. |
|
|
|
|
Application numérique avec k
= 1/5, a = 3 et b = 6. |
|
|
|
|
|
|||
|
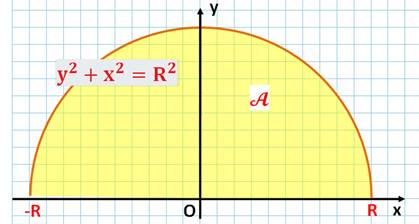
Nous allons calculer l'aire du disque en
utilisant la méthode du calcul intégral. Un bon test! Car le résultat
est bien connu. |
|
||
|
Par la méthode de
l'intégrale avec l'équation du
cercle. |
y |
|
|
|
Quelle est la fonction dont
la dérivée est celle-ci? Avec une racine, un peu de précaution. Mieux vaut
consulter une liste de primitives. |
Y |
|
|
|
L'aire est la différence de
cette fonction calculée entre R et -R. |
|
|
|
|
Les premier et troisième
termes sont nuls. Quant aux arcsinus de 1 et -1, ils valent + Pi/2 (90°) et –Pi/2 . |
|
|
|
|
Nous retrouvons bien la
relation bien connue (le double pour le disque complet). |
|
|
|
|
Nous
savons calculer des surfaces par la méthode des intégrales. Ce type de calcul
est utile pour calculer la position du centre de gravité de formes complexes
comportant notamment des arrondis. Le cas du demi-cercle
est un excellent exemple. |
![]()
|
Suite |
|
|
Intégration |
|
|
Voir |
|
|
Aussi |
|
|
Cette page |
http://villemin.gerard.free.fr/aScience/Physique/STATIQUE/CGIntegr.htm |