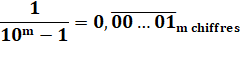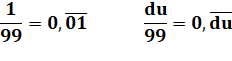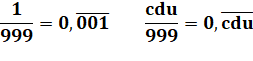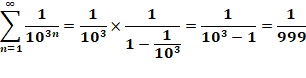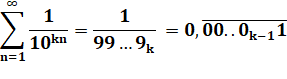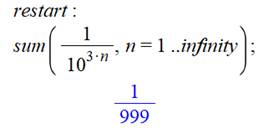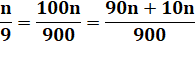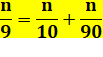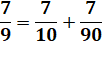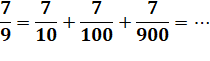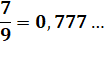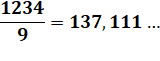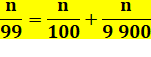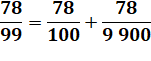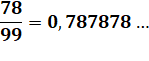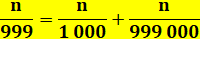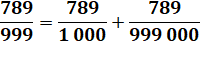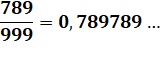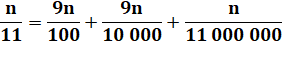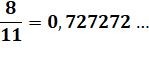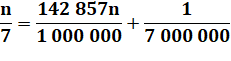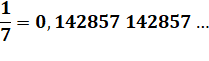|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
DIVISION par 90, 99, 999 … Calcul rapide /
Calcul mental
|
Voir Repdigits
/ 9-Repdigits
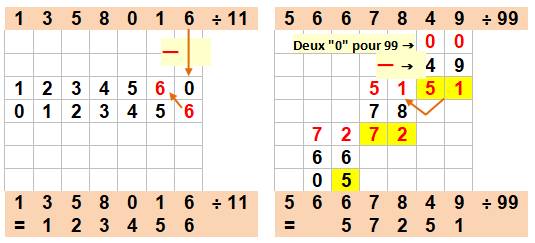
Divisions rapides par 11 et par 99, cas
sans reste
Un test de divisibilité
permet de savoir si le nombre est divisible sans reste
Divisions rapides par les 9-repdigits
|
|
|
|
|
|
Division mentale par 99


Pour n < 100, période = n et pour n ≥ 100,
centaines, suivie de la somme indiquée.
![]()
|
|
||
|
Le calcul
est rapide par simple addition cumulées des chiffres. Chaque
chiffre donne la réponse à condition de propager les retenues Pour le
dernier, on effectue la division. Voir méthode pratique en détails >>> |
2 3 1 1 2 2 2 5 6 7 9 11 2 5 6 8 0 reste 2 231122 = 25680 x 9 + 2 |
|
|
Pour une
division par 90, 900 … décaler la virgule vers la gauche d'autant de position
que de 0. |
231122 = 25680
x 9 + 2 231122 = 2568 x 90 + 2 231122 = 256,8 x 900 + 2 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Méthode rapide valable pour tout nombre Partager le nombre en groupe de deux chiffres. Ajouter le prochain groupe à la somme (y compris
retenues) que vous venez de trouver. Le reste est égal à la somme réalisée avec la
dernière somme. |
1234 / 99 = 12 reste 46 456789 / 99 = 4614 R3 = 4614,030303… Cas d'un nombre impair de chiffres 3456789 / 99 = 34917 R6 = 34917,060606… Cas d'un nombre avec des 0. Ne pas oublier que 1 devient 01 100000000 / 99 = 1010101 R1 = 1010101,010101… |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Voir Méthode
rapide, identique pour 9 / Brève
612
|
|
||
|
Division par 9 – Cas de 1/9 D'une
manière générale: Voir Nombres
périodiques |
|
|
|
Prenons m
= 3 et montrons comment passer
de l'une à l'autre des représentations |
A = 0,001 001 001 … 1000A = 1,001 001 … 1000A – 1 = A 999A = 1 |
|
|
C'est
aussi une somme infinie: |
Plus généralement
|
|
|
Avec le
logiciel Maple |
|
|
Voir Longueur
de la période d'un nombre périodique
|
Division par 9 cas de n/9 |
Écriture
particulière de la fraction qui met en
évidence une certaine répétition.
La même
opération peut être répétée sur la dernière fraction autant que l'on veut. |
C'est l'explication des décimales qui se répètent:
|
|
Division par 99 |
|
|
|
Division par 999 |
Etc. |
|
Voir Nombres
périodiques
|
|
|||
|
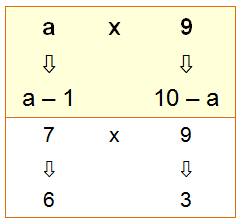
Multiplication par 9 |
Multiplication
d'un nombre à un chiffre par 9
|
|
|
|
Multiplication par 99 |
Multiplication
d'un nombre à deux chiffres par 99. Explications 100(10a + b – 1) + 100 –
10a – b 1000a + 100b – 100 + 100
– 10a – b (1000 – 10)a + (100 – 1)b 99 x 10a + 99 b 99 x (10a + b) = 99 x |
|
|
|
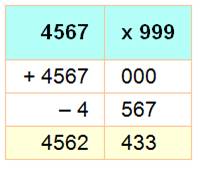
Multiplication par 999 |
Multiplication
d'un nombre à trois chiffres par 999. |
|
|
|
Multiplication par 99 …99 |
D'une manière générale,
quelle que soit la quantité de chiffres:
|
|
|
|
|
|||
|
Nombres jusqu'à quatre chiffres à
diviser par 99 Il s'agit
de nombres connus pour être divisibles par 99. Retrouvez immédiatement le
quotient. Ajoutez 1 aux deux premiers chiffres. C'est tout! Sauf pour le dernier nombre à quatre chiffres divisible par 99,
composé de quatre 9. Il faut alors ajouter 2. |
297 / 99 = 3 990 / 99 = 10 1089 / 99 = 11 2574 / 99 = 26 5445 / 99 = 55 9009 / 99 = 91 9801 / 99 = 99 9900 / 99 = 100 9999 / 99 = 101 |
||
|
Explications
Seule possibilité pour que les fractions en 99 atteignent 2: m = c = d
= u = 9 |
|||
|
Si le nombre n'est pas divisible,
calcul du reste |
R = 10 (m + d) + c + u – 99 Ex : 1095 / 99 Q = 11 et R = 10(1 + 9) + 5 – 99 = 6 11 x 99 + 6 = 1095 |
||
|
|
||||||||||||||||||
|
Nombres jusqu'à 2k chiffres à
diviser par d Il s'agit
de nombres connus pour être divisibles par d. Retrouvez immédiatement le
quotient. Ajoutez 1 aux k premiers chiffres. C'est tout! Sauf pour les nombres composés de 99. Il faut alors ajouter 2. |
36 / 9 = 4 4 455 / 99 = 45 455 544 / 999 = 456 45 665 433 / 9999 = 4 567 999 999 / 999 = 1 001 |
|||||||||||||||||
|
Division rapide par 999 idem 99 mais avec des blocs de 3 |
|
|||||||||||||||||
|
|
||
|
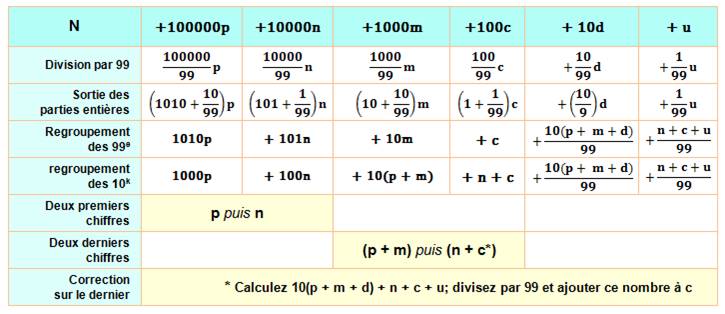
Les
choses se compliquent un peu et, évidemment, la méthode perd de l'intérêt. On
donne d'abord l'explication mathématique avant d'exposer la méthode. Explications théoriques (pour
nombres jusqu'à 1 million)
|
||
|
Exemple |
452 133 / 99 |
|
|
Chiffres
du quotient |
4 5 (4+2) (5+1) => 4 5 6 6 En cas de somme supérieure à 9, on propage la retenue. |
|
|
Calcul de
correction sur c |
10(4 + 2 + 3) + 5 + 1 + 3 = 90 + 9 = 99 => correction 1 |
|
|
Reprise
des chiffres |
4 5 6 7 = 42 133 / 99 |
|
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |