NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 02/01/2021 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Analyse
Débutants Exponentielle	EXPONENTIELLE				Glossaire Général
INDEX Arithmétique Algèbre Analyse	Introduction	Valeur	Fractions	Analogies
		Propriétés	Formules	Dénombrements
		Base	Dévelop e^x	Doublement
		Sommaire de cette page >>> Base des logarithmes naturels >>> Valeur de "e" >>> Formule pour "e"

BASE des LOGARITHMES NATURELS

Pourquoi "e" est la base des logarithmes naturels?

Cela ne semble pourtant pas si naturel que cela !

Voici un itinéraire, il y en a d'autres.

Étape 1 - Log naturels ?
Pourquoi la base "e = 2, 718…" pour les logarithmes et, en plus, les baptiser de naturels ? Pourquoi ne pas rester avec 10?	C'est une question de vitesse de croissance Avec 10, ça va trop vite Avec 2 c'est mieux Avec 1 pas possible Alors quoi ? Un peu plus de 1 Oui, c'est la bonne piste …

Étape 2 - Observations
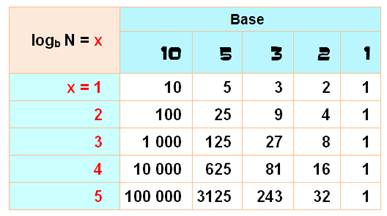
En observant le tableau ci-contre et en prenant l'exemple de log 3 et log 4. L'écart entre ces deux valeurs décroît lorsque la base du logarithme décroît	Lecture du tableau log 3 81 = 4 Exemple de décroissance En base 10 on passe de 10 000 à 1000 En base 2 on passe de 16 à 8

Étape 3 – Cherchons encore …
Si on veut gagner en densité, la lecture du tableau nous incite à descendre le plus près de la base 1, sans l'atteindre. Ça marche, quelle densité ! Ça se bouscule du côté du 1. On peut même augmenter encore la quantité de 0 de la base. Mais, enfin, les valeurs sont alors très proches les unes des autres et du 1.

Étape 4 – Dans l'autre sens
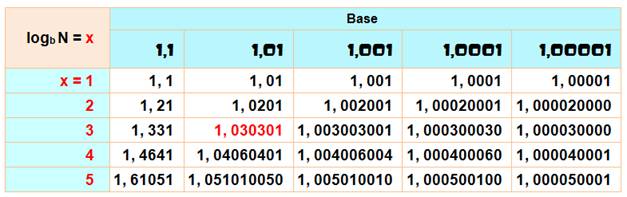
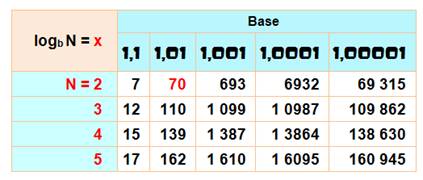
Pour mieux voir, on va chercher non pas (tableau ci-dessus). log 1,01 1, 030301 = 3 X dans la colonne et N dans le tableau. Mais, on inverse le tableau (tableau ci-contre). log 1,01 2 = 70 N dans la colonne et X dans le tableau.	log 1,01 2 = 70 log 1,001 2 = 693

Étape 5 – Encore un pas
Sur le tableau précédent, les nombres s'étalent de 7 à 160 945. On peut essayer de ramener tous les chiffres du tableau dans le même ordre de grandeur Il faut diviser par 10, puis 100, 1000, etc. Cela revient à changer la base comme indiqué.

Étape 6 – Pour conclure (enfin!)
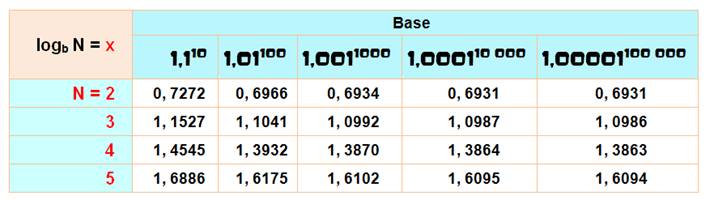
Effectivement, maintenant, tous les nombres sont voisins de 1. Calculons la valeur des bases utilisées 1,1^10 = 2, 593742460 etc. Après cette expédition, on retrouve la valeur de "e", base des logarithmes naturels.

Étape 7 – Et une formule, une!
Exprimons ces valeurs sous la forme de fractions et de puissances de 10: 1,1 = 1 + 1/10 1,01 = 1 + 1/100 etc. On retrouve notre chère formule.

Suite	Fractions exprimant "e"
Voir	Cercle Constantes Courbes élémentaires Courbe de charge d'un condensateur Exposants et puissances Exposants et puissances – Index Logarithmes Nombre d'or Pi Théorie des nombres
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Analyse/ExpoBase.htm