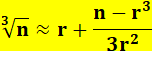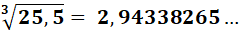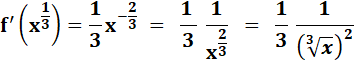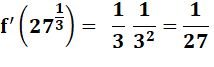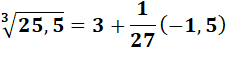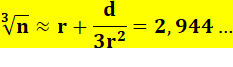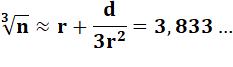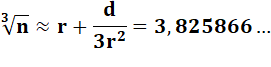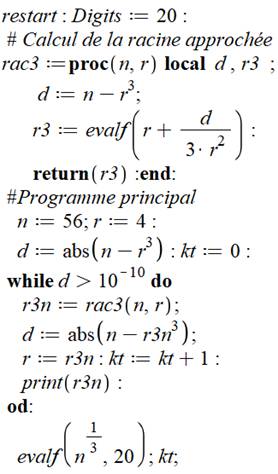|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
RACINE CUBIQUE Valeur approchée - Méthode de Newton Comment
calculer la racine cubique d'un nombre Trouver une valeur proche sans disposer
de la fonction racine cubique sur la calculatrice ? Méthode de
Newton. Règle: avec r une
valeur connue proche de la racine cubique de n.
Autre question: quelle est la fonction polynomiale qui approche la
fonction racine cubique ? |
Exemple de calcul quasi-mental
|
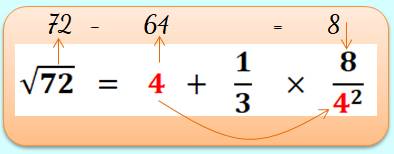
Calculez la racine cubique de 72. Elle est proche de racine cubique de 64 (43
= 64)
Ce calcul donne: 4 + 1/6 = 4,166… pour 4,160… |
Voir Courbe
montrant l'efficacité de l'approximation
|
|
|||
|
Calcul à réaliser |
|
||
|
On connait une valeur proche |
|
||
|
Quelle est la compensation pour |
25, 5 – 27 = -1,5 |
||
|
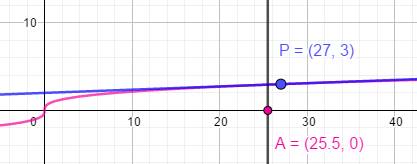
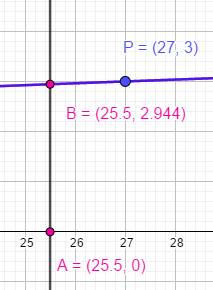
Allure de la fonction Le courbe
représentative de la fonction x3 montre que la tangente au point P
(27, 3) est pratiquement confondue avec la courbe. La pente
de la tangente est connue. C'est
la dérivée de la fonction au point P. |
Zoom
|
||
|
Comment
calculer la dérivée
? Sachant
que la racine cubique est aussi la puissance 1/3. |
Note: Utilisation
de la règle
classique de dérivation: le degré est diminué de 1 et, il devient aussi
coefficient. |
||
|
Pour x =
27 dont la racine cubique est 3. |
|
||
|
Comment
s'y prendre: la contribution des (-1,5) se fait au prorata de cette dérivée |
|
||
|
Résumé On cherche la racine cubique de n en indiquant
une racine approchée r. |
n = 25,5
r = 3 d = n – r3 =
-1,5
|
||
|
Exemple
|
n = 56 r
= 4 d = n – r3 = -8
|
||
|
Pas satisfait, on recommence |
n = 56 r
= 3,8 d = n – r3 = -0,18
|
||
|
|
But Calculer la racine cubique d'un nombre avec une
certaine précision. Procédure de calcul de la racine
cubique Après réinitialisation et demande d'une
résolution sur vingt chiffres, lancement de la procédure de calcul de la
racine avec implémentation de la formule vue plus haut. La procédure est appelée deux paramètres: le
nombre n et la racine approchée. Programme principal On fixe n
= 56 et la racine proche r = 4. Calcul de l'écart d Tant que cet écart n'atteint pas une limite
fixée, on calcule la racine cubique de n avec pour racine approchée par
itération en ré-injectant la racine tout juste calculée. On imprime le résultat du calcul pour suivre
l'évolution du calcul à chaque itération. Enfin de programme, la racine cubique calculée
directement par le logiciel est imprimée pour comparaison (en rouge). Résultat du traitement Quatre itérations auront suffit pour faire ce
calcul précis. Il suffit de régler la limite fixée au paramètre
d pour poursuivre le calcul et obtenir une précision encore plus grande. Il est très probable que le logiciel intégré
procède aussi de cette manière. |
|
|
Vitesse de convergence Avec une racine initiale r = 1 au lieu de r = 4 plus haut, il faut
10 itérations et non plus 4 pour atteindre le même résultat. Plus la
"semence" est éloignée de la racine réelle et plus la convergence est
lente. Remarque: la semence ne
doit jamais être 0, sous peine d'une division par 0. |
Voir Programmation – Index
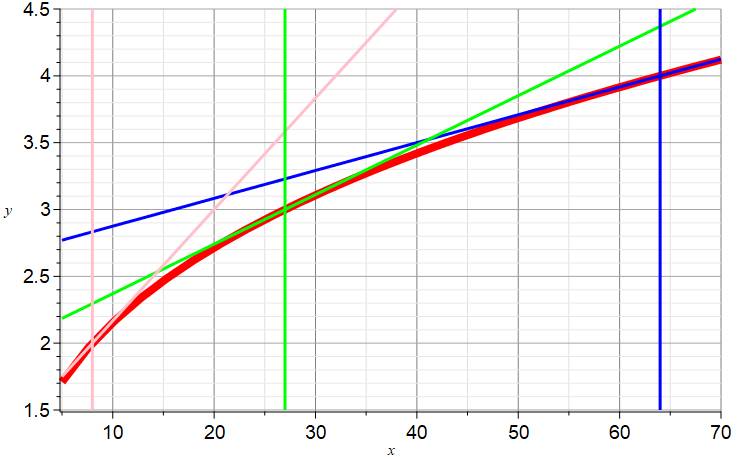
La courbe racine cubique (rouge) et trois droites selon
la formule de calcul approché pour x= 23, 33 et 43
|
|
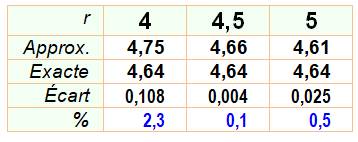
Appréciation du calcul pour racine cubique de 100
|
Pour calculer 100, les cubes les plus proches
sont 43 = 64 et 53 = 125. Constatant que 100 est, en
gros, à mi-chemin, on peut aussi choisir 4,5. Le tableau compare les performances relatives à
ses trois choix.
|
|
|
||
|
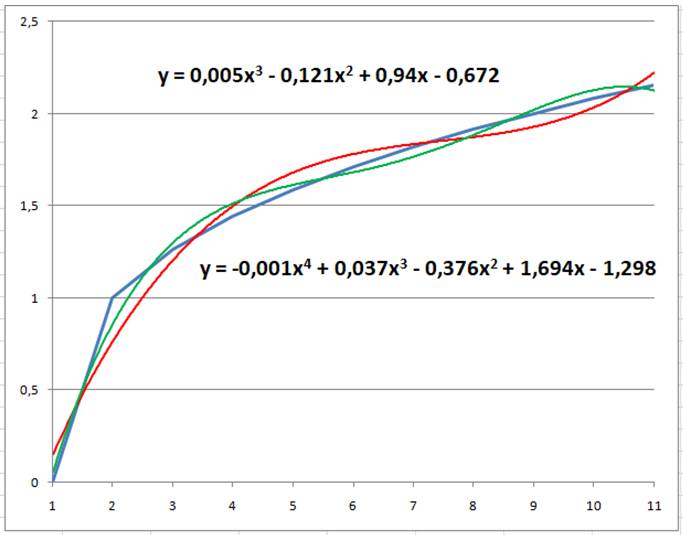
On
cherche un polynôme qui représente au mieux la fonction racine cubique dans
la zone x = {0, 10}. Une méthode pratique consiste à représenter la
courbe (bleue) sur un tableur, à partir des valeurs tablées. Dans le menu contextuel (clic-droit sur la
courbe), cochez et précisez l'ordre:
Vous obtiendrez la courbe rouge accompagnée de son
équation, et même la courbe verte avec un polynôme du quatrième degré. |
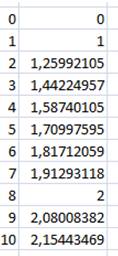
Tabulation de la fonction
|
|
|
|
||
Voir Approximation de la courbe
en S (sigmoïde)
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()