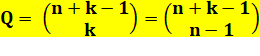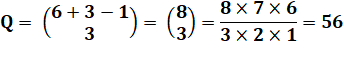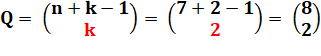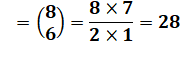|
||||||||||||||||||||||||||||||||||||||||
![]()
|
MULTIENSEMBLE, MULTISET Ensembles à répétitions Une
généralisation des ensembles qui admet la répétitions des éléments. Par
définition, un ensemble comporte un exemplaire unique
de chaque élément. Un multiensemble peut en contenir plusieurs. Analogie
avec des balles à répartir dans des sacs, paniers
ou boites. |
Anglais: Multiset, bag / Distributing balls into boxes
|
|
|||
|
Un
ensemble à répétitions ou multiensemble est un ensemble:
|
Exemples 11, 12, 21, 22 123 est équivalent à 213 ou 312 1223 n'est pas équivalent à 123 |
||
|
Cardinalité |
Quantité d'éléments Ex: Cardinalité {11223344}
= 8 |
||
|
Écritures |
{aaaaabbcddd} =
{a:5, b:2, c:1, d:3} = {a5 b2 c1 d3} Les
nombres placés derrière les lettres sont les coefficients
de multiplicité. La
cardinalité est la somme des coefficients de multiplicité. |
||
|
Factorisation des nombres |
Le nombre
123 480 se factorise
en : 2 x 2 x 2 x 3 x
3 x 5 x 7 x 7 x 7 Autrement
dit, sous la forme d'un multiensemble: {23 32
51 73} Théorème
fondamental de l'arithmétique Tout nombre peut être exprimé comme produit unique d'un multiensemble
de nombres premiers. Every positive integer can be uniquely expressed
as the product of a multiset of primes. |
||
|
Multiensemble – Définition |
Un
multiensemble est une collection d'éléments dont certains peuvent apparaître
plusieurs fois. Les
occurrences d'un élément particulier sont indiscernables. Chaque
occurrence d'un élément contribue à la cardinalité du multiensemble. La
quantité d'occurrence d'un élément donné est un nombre entier positif. La
quantité de type d'éléments peut être infinie. Un
multiensemble est complètement définit par la connaissance de ses types
d'éléments et leur fréquence. |
||
|
|
||
|
Définition Une
combinaison à répétitions et une combinaison où:
|
Exemple Le résultat du lancer de trois
dés sans distinguer lequel produit quel nombre. {1,6, 6}, {4, 2, 1},
{1, 1, 1}, etc. |
|
|
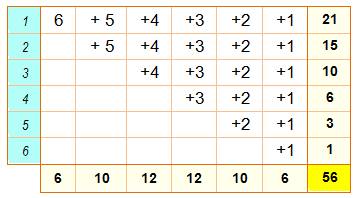
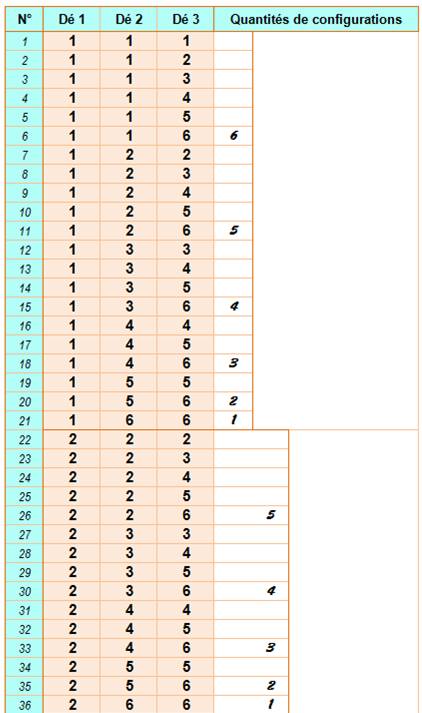
Dénombrement Une manière
de dénombrer les possibilités consiste à les énumérer. Intéressant pour
apprécier la logique de comptage. Lorsque
le premier dé donne 1 et lorsque le
deuxième dé est aussi à 1, il y a 6 possibilités pour le troisième dé.
Classique! Avec le
deuxième dé à 2, il ne faut recompter 121 qui est équivalent à 112. Par
contre 122 est nouveau ainsi que 123 etc. – Soit 5 possibilité. Avec le
même raisonnement la configuration commençant par 13 aura pour troisième dé
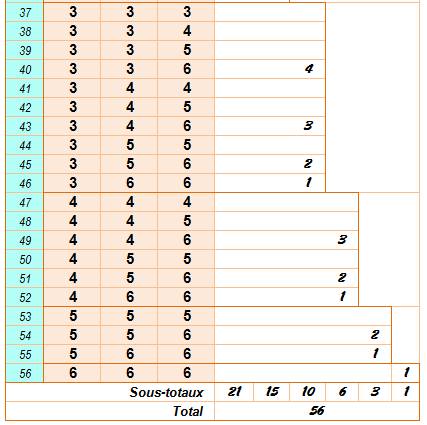
133, 134, 135 et 136. Etc. On constate que les nombres sur les dés
vont croissants, on ne retourne pas en arrière. Ainsi le
décompte est singulier Avec le 1er
dé à 1: 21 possibilités. Avec le 1er
dé à 2: 15 possibilités. Etc.
La
formulation n'est pas évidente avec cette méthode directe. |
Cas du lancer de trois dés
|
|
|
Formule La
méthode des étoiles et des barres permet
d'établir la formule générale:
Les
parenthèses sont les coefficients
du binôme. |
Exemple Avec n =
6 chiffres et k = 3 dés:
|
|
|
|
|
|
Notations
|
|
Anglais: Counting multisets, multichoose coefficient
|
|
||
|
Combien
de sortes de dominos?
Autrement-dit: dénombrer l'ensemble des dominos de taille 2x1? Il s'agit
de calculer le nombre de combinaisons avec
répétitions de 2 chiffres parmi 7. |
n = 7 et k = 2
|
|
|
|
||
|
Dans
l'Antiquité, on manipulait des multiensembles sans le savoir: collection de
symboles pour représenter les nombres (comme les dessins
de bâtons). Richard Dedekind (1831-1916): une notion
utile consiste à affecter une fréquence à
un élément pour indique combien de fois il doit être compté comme élément de
l'ensemble. Karl Weierstrass (1815-1897) avait
une curieuse façon de concevoir les nombres. Par exemple 0,543 est un nombre
qui contient 1/10 avec la multiplicité 5; 1/100 ave le multiplicité 4; etc. En 1895,
Cantor définit l'ensemble à élément unique: "aggregates" consist
only of distinct elements. |
Hermann Weyl (1885-1955) définit les
"agrégats" qui peuvent comporter plusieurs éléments du même type et
les utilisent pour traiter des problèmes de physique, chimie et génétique. Parker-Rhodes
développe une théorie mathématique qui traite des multiensembles. Sa théorie
généralise la théorie des ensembles tout en l'englobant. D'autres
mathématiciens, comme Knuth, utilisent les multiensembles comme outil
pratique pour développer des algorithmes
numériques. En 1976,
Lake propose une axiomatique des multiensembles fondée sur les développements
de von Neumann en théorie des
ensembles (1925) Le terme
multiensemble ou multiset en anglais est de facture récente. En anglais, on
trouvait les termes: bag, bunch, fireset … |
|
|
|
|
|
A multiset
is a collection of objects (called elements) in which elements may occur more
than once. The number of times an element occurs in a multiset is called its multiplicity. The cardinality
of a multiset is the sum of the multiplicities of its elements. MST: Muliset théory mset: abbreviation of multiset.
|
|
![]()
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/Denombre/aaaBalle/Multiset.htm
|
![]()