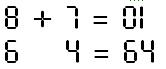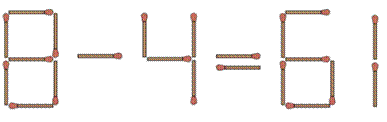|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
ALLUMETTES – Géométrie
|
Anglais: Matchstick construction
Devinette pour soirée au coin du feu …
|
Comment
faire une croix avec une allumette sans la briser? Indice: l'image
ci-dessus devrait vous mettre sur la voie. Solution:
la faire brûler et dessiner une croix avec la partie carbonisée. |
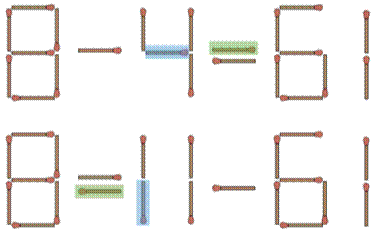
Pour se lancer: déplacer une allumette pour
rétablir l'égalité
|
|
|
|
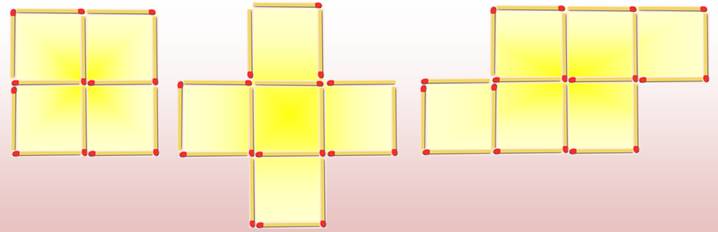
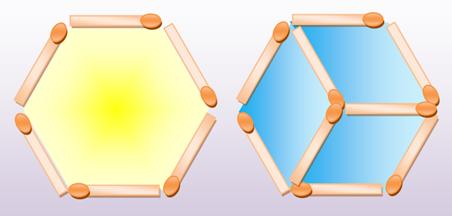
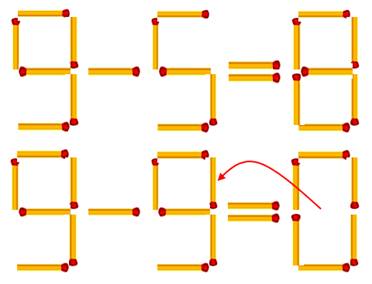
Énigme Pour ces trois figures,
déplacer simplement quatre allumettes et obtenez trois carrés
ou trois rectangles.
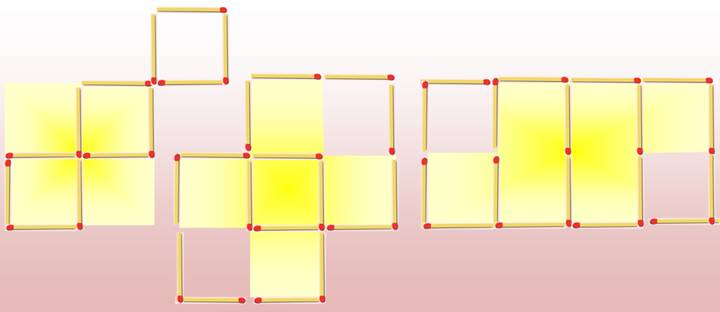
Solutions La zone en jaune témoigne de
la figure originelle.
|
|
|
|
|
|
T.R.
Dawson, célèbre pour ses problèmes d'échecs, découvrit que:
Les constructions à la règle et au compas sont possibles si, et seulement si, elles le sont avec des allumettes
identiques. |
|
Voir Constructibilité
|
|
|
|
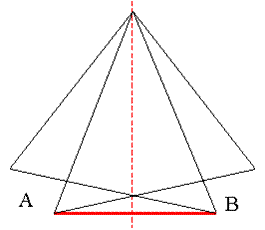
Bissection d'un segment
avec des allumettes: Il suffit de sept allumettes. Chaque
segment (hors AB) est une allumette. La
droite en pointillés rouges est même la médiatrice de AB.
|
|
|
|
||||||||||||||||
|
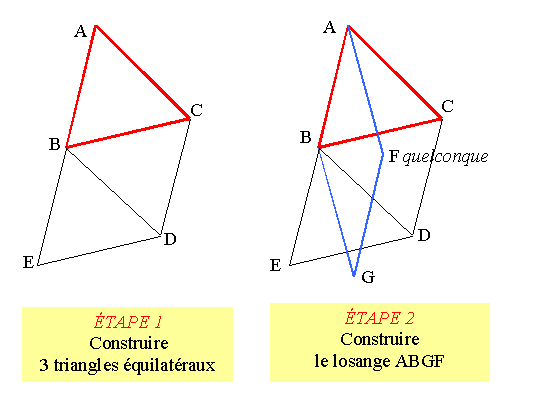
Avec
6 allumettes, combien peut-on construire de
triangles équilatéraux ?
1 Astuce: passage en
trois dimensions. 2 Astuce: vision dans un miroir. Astuce
douteuse car toujours applicable. Avec un second miroir, il y aurait même
multiplication infinie!
|
||||||||||||||||
|
|
|
|
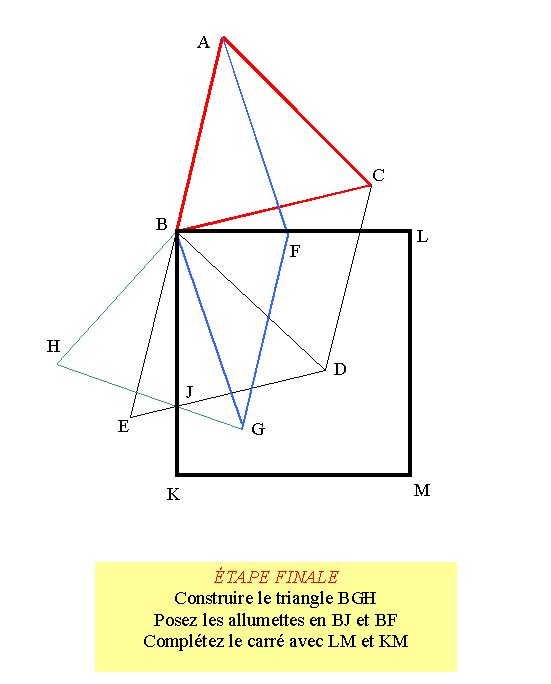
Construction
du carré avec des allumettes.
|
|
|
|
|
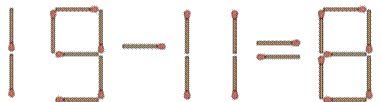
Deux allumettes déplacées Comment rétablir l'égalité en déplaçant seulement
deux allumettes. Solution Barre horizontale du 4, pour faire 11 Barre du signe égal pour délacer ce signe égal. L'égalité est rétablie ! Autres solutions: D'après Simon
Khan Voir Nombres
strobogrammatiques |
|
|
![]()
|
Voir |
|
|
Découverte Junior |
|
|
Cette page |
![]()