|
||||||||||||||||||||||||||||
![]()
|
CYLINDRE Problèmes typiques posés au
brevet. Note: la valeur numérique de Pi est notée 3,14 alors que les calculs sont
effectués avec toute la précision de la calculette. |
|
|
||
|
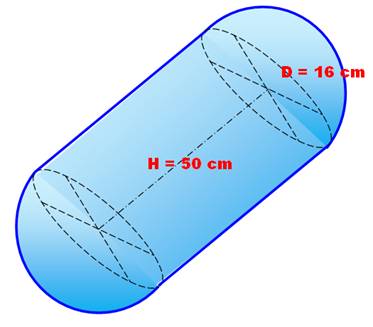
Problème Calculez le volume du boudin
formé d'un cylindre et terminé par deux demi-boules. Indice Les deux demi-sphères sont
équivalentes à la sphère complète. Le volume du boudin est donc
égal à la somme des volumes du cylindre et celui
de la sphère. Remarquez que l'on nous
donne la longueur du diamètre
et non celle du rayon. |
|
|
|
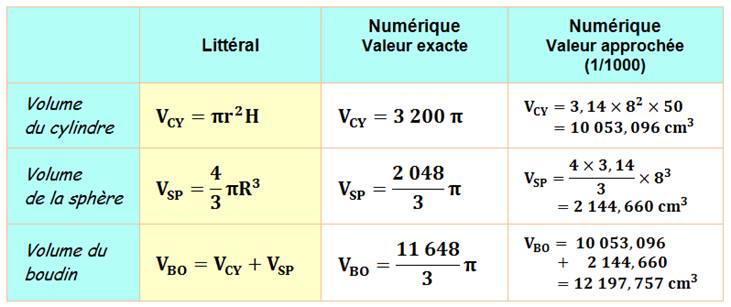
Solution
Le
volume du boudin arrondi au centième est égal à: 12 197, 76 cm3. |
||
Brevet Amérique du Nord
2014
|
|
||
|
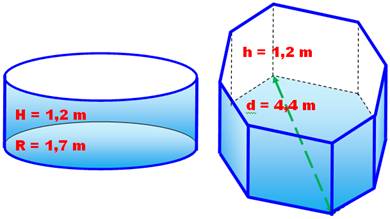
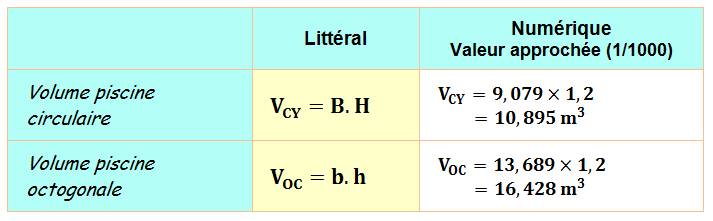
Problème Deux piscines: l'une de base
circulaire et l'autre de base octogonale. 1. Si la construction ne dépasse pas une occupation du sol de 10 m²,
aucune formalité administrative (permis de construire) n'est demandée. Est-ce
le cas pour ces deux piscines? |
|
|
|
2. Si la surface minimale recommandée par baigneur est de 3,4 m², quelle est
la piscine convenable pour une famille de quatre personnes? 3. Le débit de remplissage est de 12 litres par minutes. Avec une ouverture du robinet
du vendredi 14h 00 au samedi matin 10h 00, est-ce que les piscines vont
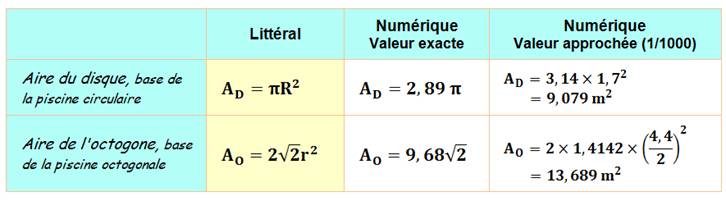
déborder? Solution 1 Pour connaître la surface
d'occupation du sol, il faut calculer l'aire de la base de chaque piscine:
l'aire du disque et
l'aire de l'octogone.
La piscine circulaire peut
être construite sans formalité (< 10 m²); ce n'est pas le cas de la
piscine octogonale. Solution 2 Avec quatre personnes, la
famille requière 4 x 3,4 = 13,6 m² Ça passe juste avec la
piscine octogonale, mais certainement pas avec la circulaire. Solution 3 Cette question nécessite le
calcul du volume des piscines:
Note: Voc = 16,42750474 arrondi à 16,428 (de justesse!) Durée d'ouverture du
robinet: de 14 h à minuit = 10 h et de minuit à 10 h, encore 10h; soit 20
heures au total. Volume d'eau débitée: 20 h x
60 min/h x 12 l/min = 14 400 litres = 14, 4 m3 La piscine circulaire
déborde, mais l'octogonale n'est pas encore pleine. Sa hauteur de remplissage
est égale à hr = Volume / Base = 14,4 / 13,689 = 1,052 m |
||
Brevet Polynésie 2014
|
|
||
|
Problème
|
|
|
|
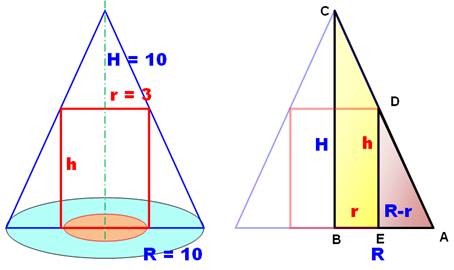
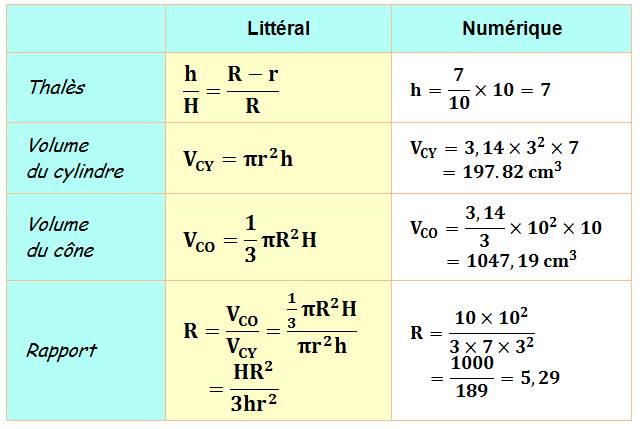
Solution Les triangles ABC et ADE ont
un angle commun A; des côtés parallèles BC et DE; ils sont semblables. Le théorème de Thalès permet de calculer h en
fonction de R, r et H.
|
||
|
|
||
|
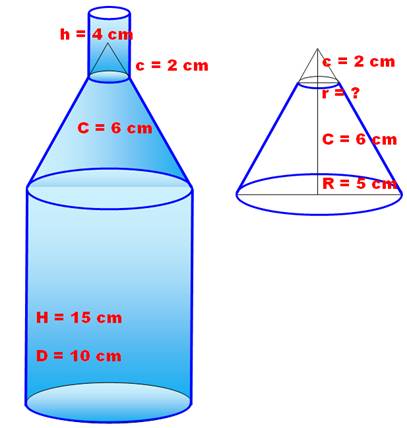
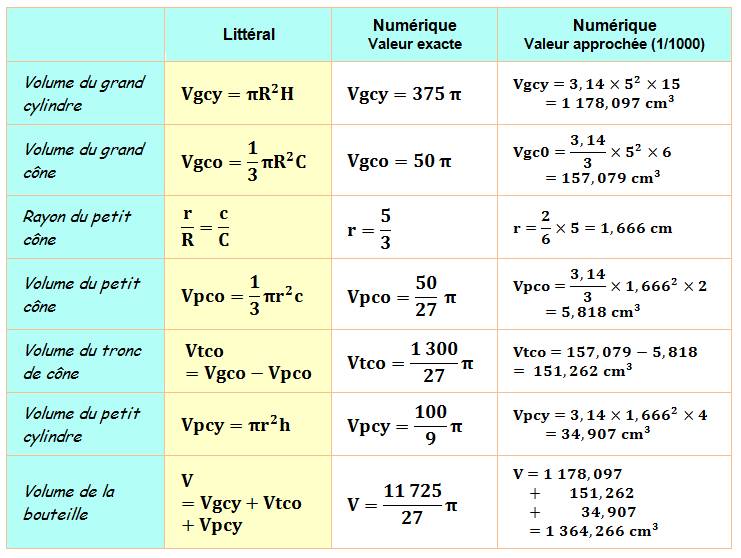
Problème Une bouteille formée d'un grand
cylindre, d'un tronc de cône et surmonté d'un petit cylindre. Quel est le volume de la
bouteille? Indice Le volume du tronc de cône
est égal au volume du grand cône diminué de celui du petit cône. Le rayon du petit cône
(r) par rapport au rayon du grand cône
(R) est dans la même proportion que les hauteurs (r / R). Voir figure de
droite. |
|
|
|
Solution
|
||
Brevet Pondichéry 2014
![]()
|
Retour |
|
|
Aussi |
|
|
Cette page |
![]()