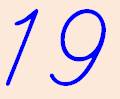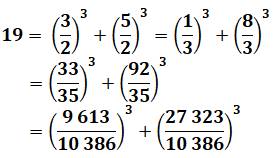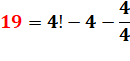nombre dix-neuf et maths

Édition du: 04/11/2024

DicoNombre Débutant Glossaire Types de nombres Nom des nombres Écriture des nombres Table des facteurs Langues	Dictionnaire des Nombres
	… / 0,001 / 0,1		0 à 99			100 / 200 / 300 / 400 / 500 / 600 / 700 / 800 / 900 / 1 000 / 2 000 / 5 000 / 10 000 / 100 000 / 10⁶ / 10⁹ / 10¹⁰⁰ / Infini
	-0-	10		20	30		40	50	60	70	80	90
	10	11		12	13		14	15	16	17	18	19

Nombre 19

Culture 19

Maths 19

Expressions avec 19

Dix-neuf

Nineteen

Nouvelle orthographe

avec des traits d'union partout

Facteurs
Binaire	1 0011
Bases	34₅
Romain	XIX

Suite

Nombre réversible

Caractérisation du nombre

Coster

Déficient

Factorielle alternée

Fortuné

Heegner

Heureux

Impair

Keith

Lucas premier (rang)

Nombre de Mersenne (Exposant)

Palin10 (1 + 9 = 10) – Le plus petit

Premier

Premier cubain

Premier de Chen

Premier de Pierpont

Premier inévitable (ou minimal)

Premier irrégulier d'Euler

Premier faible

Premier jumeau avec 17

Premier long

Premier minimal ou inévitable

Premier régulier

Premier supersingulier

Strictement non palindrome

Voir

Nom des nombres

Nombres selon langues

Nombres selon bases

Fonctions arithmétiques

Triangulaire centré

Hexagonal centré

Octaédrique

Rappel Propriétés générales >>>

Chiffres et numération

Nombre et son retournement à 180°sont premiers.
Vrai pour 199 et 661; 1999 et 6661.

Faux pour le suivant.

19 × (1 + 9) = 190 = T₁₉

Devient triangulaire lorsque multiplié par la somme de ses chiffres.

19 = 9 + 5 + 5 = 95 / 5

Mêmes chiffres de part et d'autre de l'égalité.

19 = (1x9) + (1+9)

19² = 361

19 = (1x9) + (3+6+1)

19⁴ = 130 321

19 = (1x9) + (1+3+0+3+2+1)

Nombre égal à produit des chiffres + somme des chiffres, comme tous les nombres à deux chiffres terminés par 9.

Aussi avec les chiffres du carré et ceux du biccarré.

19, 110, 121

Le plus petit palindrome retard d'ordre 2.

Prendre le nombre, lui ajouter son retourné

Recommencer jusqu'à obtenir un palindrome.

N'est repdigit dans aucune base. Il n'est pas brésilien.

19 = 1 x 9 + 1 + 9

29 = 2 x 9 + 2 + 9

129 = 12 x 9 + 12 + 9

Tout nombre terminé par 9 est de la forme: 9k + k + 9.

19 = (1 x 9) + (1 + 9) = 9 + 10

29 = (2 x 9) + (2 + 9) = 18 + 11

…

99 = (9 x 9) + (9 + 9) = 81 + 18

Nombres calculés avec leurs propres chiffres.

C'est le cas pour tous les nombres à deux chiffres terminés par 9:

10d + u = du + d + u

u = 9 quel que soit d.

Addition et soustraction

p(19) = 490	Quantité de partitions du nombre.
19 = T₂+ T₃ + T₄ = 3 + 6 + 10	Somme de nombres triangulaires consécutifs.
19 = 4! – 3! + 2! – 1!	Somme alternée de factorielles.

Multiplication, division, diviseurs

19-Harshad = [114, 133, 152, 171, 190, 209, 228, 247, 266, 285, 399]		Ces onze nombres sont 19-Harshad. Quotient 19 lorsque divisés par la somme de leurs chiffres. Rare.
19 est premier 21 = 3 x 7 est semi premier	Nombre Premier de Chen.
1 + 9 = 10 et 1 + 0 = 1	Première racine numérique nécessitant deux opérations.
19 = 3 + 5 + 11	Plus petit nombre impair non divisible par 3, somme de trois impairs distincts.
19 mod 9 = 1 29, 39, 49, 59, 69, 79 et 89	Nombre modeste: on retrouve tous ses chiffres dans cette opération. Ces autres nombres en 9 ont la même propriété.
1, 9, 10, 19	Nombre de Keith, le plus petit premier.
19 = 4! – 3! + 2! – 1!	Factorielle alternée.
1² + 9² = 82 9² + 81 = …	Séquence de Keith avec racine carrée de la somme des carrés. En partant de 19, le nombre entier 67 apparaît après 9 sommes

Divisibilité par 19

Ajoutez deux fois les unités aux dizaines et itérez.

2 337 => 233 + 14 = 247 => 24 + 14 = 38 qui est divisible par 19.

6700 => 670 + 0 = 670 => 67 + 17 = 94 => 9 + 8 = 17 non divisible.

Voir Critères de divisibilité / Divisibilité par 19.

19 abcdefghi abcdefghi

Ex: 123456789123456789 / 19

= 6497725743339831

114114114114114114 / 19

= 6006006006006006

Un nombre de neuf chiffres répétés est divisible par 19.

19 = 510 529 – 510 510

Nombre fortuné: différence entre primorielle et le premier juste plus grand (d'au moins 2).

19 | Groupe monstre

Premier supersingulier. Il divise le groupe monstre.

Avec les puissances

19 = 1² + 3² + 3² = 1² + 1² + 1² + 4² = 1² + 1² + 2² + 2² + 3² = 1³ + 1³ + 1³ + 2³ + 2³ = 1⁴ + 1⁴ + 1⁴ + 2⁴	Seule somme de puissances de 2 à 5 avec deux à cinq termes.
19 = 10² – 9² = 10 + 9	Différence de deux carrés de nombres consécutifs. Motif général pour tous les nombres impairs.
		Sommes de deux cubes rationnels.
19 = 7³ – 18² = 343 – 324	Seul cas d'équation de Bachet pour k = 19. Différence entre un cube et un carré.
19 = 3³ – 2³ = 6 x 3 + 1	Nombre binomial. Premier, différence de deux cubes successifs (nombres cubains); tous la forme 6k + 1
19 = 7³ – 18² = 10² – 3⁴ = 12² – 5³	Différence entre puissances.
19 = 32 – 3² – 2² = 53 – 5² – 3² = 72 – 7² – 2²	Curiosité, il y en d'autres.
19 = 3² + 3² + 1² 19³ = (19 x 3)² + (19 x 3)² + (19 x 1)² = 57² + 57 ² + 19² 6 859 = 3 249 + 3 249 + 361 Aussi 19³ = 69² + 37² + 27² 6 859 = 4 761 + 1 369 + 729			Curiosités
	Le produit de quatre nombres consécutifs plus 1 est un carré.

En puissance

19² = 361

Exemple de concaténation de deux premiers (3 et 61) formant un carré.

19² × 2 = 722

2-super 2 nombre ou hyper 2.

19² + 180² = 181² = 32 761

Triplet de Pythagore avec b >> a.

19³ = 6 859 & 6 + 8 + 5 + 9 = 28

28³ = 21 952 & 2 + 1 + 9 + 5 + 2 = 19

Curiosité réciproque avec des cubes.

19⁴ = 130 321

Bicarré avec chiffres jusqu'à 3.

19		1+9	= 10
19²	= 361	3+6+1	= 10
19⁴	= 130 321	1+3+0+3+2+1	= 10

Même somme des chiffres.

Voir 468 et 585

p = 19 est premier et la fraction est un nombre entier et premier.

Liste de tels nombres avec p = (2, 3, 19, 31, ?).

Dénombrement, jeux et curiosités

19 fois avec le chiffre 9 (ou un autre) dans la plage 1 à 99		Il y a 19 nombres comportant au moins une fois le chiffre 9 entre les nombres 1 et 99. Il y a 20 fois le chiffre 9 dans cette plage. C'est le nombre 99 qui fait la différence. Voir Formule générale
19 nombres à la puissance 4		Théorème de Waring: tout entier est décomposable en somme d'au plus 19 puissance quatrième. Le nombre 79 exige les 19 termes.
19	Il existe 19 polynômes unitaires de degré 3 à coefficients entiers dont les racines sont dans le disque unité. Ex: z³ + 1 ou z³ – 1.
		Jeu du quatre 4.

Géométrie

19 régions créées par les côtés prolongés de l'hexagone.

>>>

Autour du nombre

– 19		Nombre de Heegner.
R₁₉ = 111…11_{19 fois}		Un des rares repunits premiers Ils sont cinq connus:
M₁₉ = 2¹⁹ – 1 = 524 287			Nombre de Mersenne premier.
1 / 19,602 = 0,05 10 15 …			Suite des multiples de 5.
e¹⁹ – E = 0,0368			Exponentielle proche d'un entier.
19	Plus petit indice de la suite 6-Gödel à être non-entier.
				Nombre premier long. La période du développement décimal de la fraction est maximale en une seule suite permutée pour toutes les fractions avec ce dénominateur.