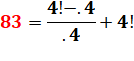NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 05/11/2024 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
Débutants Général	DicoNombre NOMBRES				Glossaire Général
82 81 80 79 / 78 75 / 70 60 50 40 30 20 10	83				84 85 86 87 90 100 500 1000 1 million
Nombre 83		Maths	Culture	Numération 80 à 89

CARTE D'IDENTITÉ
Nombre	Premier	Département	VAR
Facteurs	83 = 1 x 83	Élément	BISMUTH Bi
Propriétés Typiques	/	Mnémo	FEMME
	Suite Maths		Suite Culture

Propriétés CULTURELLES

Quatre-vingt-trois

Quatre-vingt-troisième

Voir Orthographe des nombres

Espagnol Italien	Anglais Allemand
ochenta y tres ottantatre	eighty-three dreiundachtzig

Voir Numération 80 à 89

Nombres et langues

Nombre	83 nombres premiers résistants par la droite.	>>>
Religion	83 vies chez les Hindouistes.	>>>
Social	83,8 ans Espérance de vie des femmes en France en 2005.	>>>

Propriétés MATHÉMATIQUES

Facteurs	83 = 1 x 83
Diviseurs	1, 83
Quantité	2
Somme	84
S - N	1

Déficient

Impair

Narcissique de Keith

Premier de Bertrand

Premier de Chen

Premier de Sophie Germain

Premier faible

Premier n°23

Premier régulier

Premier résistant

Premier sexy

Premier sûr

Wieferich avec 83

Voir Nom des nombres

Voir Nombres géométriques

Chiffres et numération

83	N'est repdigit dans aucune base. Il n'est pas brésilien.
8310 = 3825	Exactement les mêmes chiffres en base b.
83 + 38 = 121 = 11² 83 – 38 = 45 = T9	Devient palindrome et carré en lui ajoutant son retourné. Triangulaire en lui retirant.
83 = 4+7+4+5+8+3+2+1 + 2+2+5+2+2+9+2+2+3+2+1+3+9+0+4+1 = 8+3 + 6+8+8+9 + 3+9+3+9+0+4+0+6+4+3 83^2 = 6 889 83^4 = 47 458 321 83^5 = 3 939 040 643 83^8 = 2 252 292 232 139 041		Narcissique de Keith Somme avec ses chiffres et ceux de ses puissances. Voir Table des nombres de Keith

Addition et soustraction

83 = 11 + 13 + 17 +19 + 23 = 23 + 29 + 31	Somme de premiers consécutifs. Voir Table
83 première solution pour =>	Trois nombres auxquels on ajoute k. Alors, le premier vaut trois fois la somme des autres, le deuxième quatre fois et le troisième cinq fois. La valeur minimale est 83 et ces trois nombres sont (7, 13, 17). Voir Nombre 73 pour explications

Multiplication, division, diviseurs

83 est premier 85 = 5 x 17 est semi-premier	Nombre premier de Chen.
2 x 83 + 1 est aussi premier	Nombre premier de Sophie Germain.

Motif infini: les deux chiffres (8 et 3) se retrouvent encadrant le produit

Ex: 83 x 41 096 = 3 410 968

Voir Pépites

Le plus petit nombre tel que son totient (phi) atteint 2 après six itérations.

Avec les puissances

83 = 1² + 1² + 9² = 3² + 5² + 7² = 1^4 + 1^4 + 3^4	Somme de puissances.
83 = 42² – 41² = 42 + 41	Motif général pour tout nombre impair.
83 = 4^3 + 3^3 – 2^3 = 64 + 27 – 8	Somme de trois cubes de nombres consécutifs.

En puissance

83 et 4 871	Paire de Wieferich.
83² = 6 889 et 6 + 8 + 8 + 9 = 31	Somme maximale atteinte par les chiffres d'un carré d'un nombre à deux chiffres. Plus petit carré contenant deux "8".
2^83 = 9 671 406 556 917 033 397 649 408	Plus petite puissance de 2 avec une suite de trois 3 de suite.

Autour du nombre

Toutes les fractions avec 83 au dénominateur possèdent 41 décimales répétitives en deux suites permutées.
	Nombre pour lequel la série harmonique dépasse la valeur 5.
F83 = 99 194 853 094 755 497	Ce nombre de Fibonacci est premier.

Jeux et curiosités

Jeu du quatre 4. Avec .4 = 0, 4 = 2/5

Identité détaillée

Voir Diviseurs, Quantité, Somme, Fonctions arithmétiques

Numération: base, [chiffres]			Repdigit (Brésilien)
2, [1, 0, 1, 0, 0, 1, 1] 3, [1, 0, 0, 0, 2] 4, [1, 1, 0, 3] 5, [3, 1, 3] 6, [2, 1, 5] 7, [1, 4, 6] 8, [1, 2, 3] 9, [1, 0, 2] 10, [8, 3] 11, [7, 6]	12, [6, 11] 13, [6, 5] 14, [5, 13] 15, [5, 8] 16, [5, 3] 17, [4, 15] 18, [4, 11] 19, [4, 7] 20, [4, 3] 21, [3, 20]	22, [3, 17] 23, [3, 14] 24, [3, 11] 25, [3, 8] 26, [3, 5] 27, [3, 2] 28, [2, 27] 29, [2, 25] 30, [2, 23] 60, [1, 23]	82, [1, 1]

Voir Bases / Brésiliens

Suite	Nombre 84 Voir en haut de page DicoNombre
Cette page	http://villemin.gerard.free.fr/NombDico/Nb50a100/Nb83.htm