|
|||||||||||||||||||||||||||||||||||||||
![]()
|
DIVISEURS d'un NOMBRE Facteurs et diviseurs / Facteurs premiers /
Diviseurs propres Ne pas confondre ces notions. Où il est question du Théorème fondamental de l'arithmétique. Avec cette page, on apprend à identifier les diviseurs des nombres. Les pages suivantes, bâties sur le même modèle, montreront comment
calculer la quantité de diviseurs, leur somme, et leur produit. |
Voir Diviseurs –
Tables
|
|
|
|
Théorème fondamental de l'arithmétique (TFA) Tout nombre entier
naturel est décomposable de façon UNIQUE en produit
de ses facteurs premiers,
sans compter les permutations. Anglais:
fundamental theorem of arithmetic, unique factorization theorem or unique-prime-factorization
theorem. Allemand: Primfaktorzerlegung (Zerlegung =
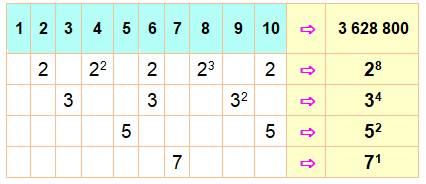
décomposition). Exemple Le nombre factorielle
10 = 10! = 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10 = 3 628 800 est en fait le produit des facteurs premiers: 28
x 34 x 52 x 7 Passage du produit aux facteurs premiers
Voir Liste des facteurs
des nombres / Démonstration de
ce théorème |
|
|
Facteurs premiers |
Diviseurs |
|
Atomes des nombres. Élément de
base des nombres. Composition
unique (TFA). Incroyable: chaque nombre est caractérisé par cette combinaison.
C'est son empreinte digitale. |
Combinaison
des atomes qui divisent le nombre. Ce sont
tous les produits possibles des
facteurs premiers entre eux. Les
diviseurs sont plus nombreux que les facteurs premiers. |
|
12 = 2 x 2 x 3 =
2² x 3 |
12 est divisible par 1, 2, 3, 4, 6, 12 |
|
12 possède
2 facteurs premiers |
Il a 6 diviseurs |
Voir Facteur et
diviseurs – Définitions
|
|
||
|
Facteurs ou diviseurs premiers Sans autre
indication, facteurs signifie: facteurs
premiers. On utilise
parfois le vocable: diviseurs premiers. Exemple avec le nombre15 Facteurs: {3, 5} Diviseurs premiers: {3, 5} Le produit
des facteurs est appelé radical
du nombre. Rad(15) = 3 x 5 = 15; Rad(12) = 2 x
3 = 6 |
Diviseurs et diviseurs propres Sans autre
indication, diviseurs signifie diviseurs,
y compris le nombre. Sinon on
précise: diviseurs propres, excluant le nombre lui-même Exemple avec le nombre15 Diviseurs (15) = {1, 3, 5, 15} Diviseurs propres (15) = {1, 3, 5} |
|
|
Définition Nombre dont la moyenne des diviseurs
est un nombre entier. Nombre dont la somme des diviseurs (sigma) est divisible par la quantité
(tau) de diviseurs:
Exemple:
Div(2 019)
= {1, 3, 673, 2 019} => Moyenne = 2 696 / 4 = 674 Liste: 1,
3, 5, 6, 7, 11, 13, 14, 15, 17, 19, 20, 21, 22, 23, 27, 29, 30, 31, 33, 35,
37, 38, 39, 41, 42, 43, 44, 45, 46, 47, 49, 51, 53, 54, 55, 56, 57, 59, 60,
61, 62, 65, 66, 67, 68, 69, 70, 71, 73, 77, 78, 79, 83, 85, 86, 87, 89, 91,
92, 93, 94, 95, 96, 97, 99, 101, 102, 103, 105, 107, 109, 110, 111, 113, 114,
115, 116, 118, 119, 123, 125, 126, 127, 129, 131, 132, 133, 134, 135, 137,
138, 139, 140, 141, 142, 143, 145, 147, 149, 150, 151, 153, 154, 155, 157,
158, 159, 161, 163, 164, 165, 166, 167, 168, 169, 173, 174, 177, 179, 181,
182, 183, 184, 185, 186, 187, 188, 189, 190, 191, 193, 195, 197, 198, 199,
201, 203, … Suite voir liens |
|
|
|||||||||||||||||||||||||
|
Nous
savons qu'un nombre
premier p n'est divisible que par 1 et lui-même. On
remarque vite que les diviseurs d'un nombre premier sont: 1 et p. On
adopte la présentation ci-contre qui va nous
permettre de considérer des cas de plus en plus généraux en utilisant une
procédure quasi automatique. |
Illustration
Formalisation
Exemples
|
||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||
|
Jusque là,
identifier les diviseurs, c'est facile!
Quantité de diviseurs: Avec les
nombres premiers: il y en a 2. Et avec
les nombres, produits de deux facteurs premiers: il y en a 4. |
Illustration
Formalisation
Exemples
|
||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
Avec les
puissances de nombres premiers, on va trouver plus de diviseurs. En fait
autant que de puissances de 0 à la puissance maximale a, soit a + 1
diviseurs. |
Illustration
Formalisation
Exemples
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Avec les
puissances de nombres premiers, les diviseurs sont:
Avec un
produit de puissances, ce sont les mêmes, combinés avec le nouveau facteur et
ses puissances:
|
Illustration
Formalisation
Exemples
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
Exemple et idée de disposition des nombres pour les trouver tous |
|
|||||||||||||||||||||||||||||||||||||||||||
|
On cherche d'abord les diviseurs du premier bloc de facteurs |
|
|||||||||||||||||||||||||||||||||||||||||||
|
Avec le deuxième bloc de facteurs |
|
|||||||||||||||||||||||||||||||||||||||||||
|
Avec le troisième bloc de facteurs Cette
disposition semble pratique pour identifier TOUS les diviseurs. On peut
les compter facilement et, même en faire la somme. Voyons
cela, et essayons de trouver les lois générales. Vous serez
épatés de réaliser que c'est assez simple. |
|
|||||||||||||||||||||||||||||||||||||||||||
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
|
|
|
Cette page |
http://villemin.gerard.free.fr/Referenc/Prof/APROF/DivVal.htm
|
![]()