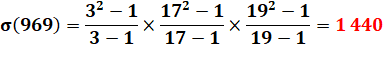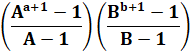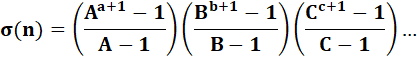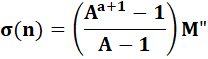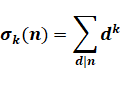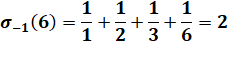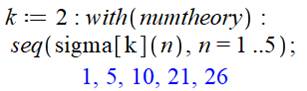théorie des nombres - calcul de la somme des diviseurs d'un nombre

NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 08/07/2023 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Introduction à la Théorie des nombres
Débutants Division	DIVISEURS				Glossaire Division
INDEX Accueil Sommaire	Introduction	Valeurs	Quantité	Somme
	Produit	Comparaisons	Som-Prod	S = somme, n = ?
	Terminale	Sommaire de cette page >>> Exemple avec le nombre 969 >>> Somme et quantité >>> Somme et nombre premiers entre eux – Duffy >>> Nombre premier >>> Produit de 2 facteurs premiers >>> Puissances >>> Produit de puissances >>> Théorème général >>> Table des sommes des diviseurs et de leurs cumuls >>> Fonction diviseur – Généralisation

SOMME des DIVISEURS

Selon la somme de ses diviseurs, un nombre entier est parfaits, déficients ou abondants.

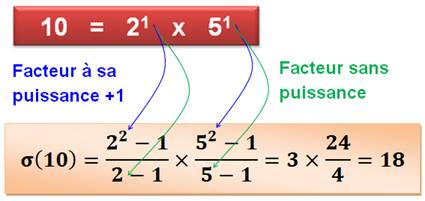
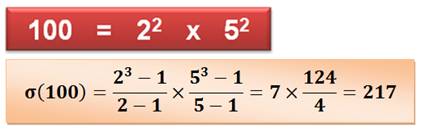
Mais, comment calculer la somme des diviseurs d'un nombre entier (n)? Vous connaissez la factorisation de ce nombre, alors vous savez facilement calculer la somme des diviseurs.

Exemple pour 10. La somme de ses diviseurs est 18 = 1 + 2 + 5 + 10.

On effectue autant de divisions que de facteurs. Au numérateur un de moins que le facteur à la puissance +1; et au dénominateur le facteur sans puissance diminué de 1.

La lettre grecque se lit sigma de 10.

Voir Diviseurs – Tables

Exemple avec le nombre 969
Factorisation La factorisation de 969 est délicate. Bien sûr, ce nombre est divisible par 3. Une recherche plus approfondie doit être faite jusqu'à des facteurs possibles jusqu'à de l'ordre de 20 (racine de 400 > 323). En effet, une recherche rapide sur tableur montre que 323 = 17 x 19.		Divisible par 3 969 = 3 x 323 Recherche d'autres diviseurs
Identification des diviseurs Les diviseurs uniques Les diviseurs résultat de la multiplication de deux facteurs, puis Les diviseurs résultat de la multiplication de trois facteurs		1, 3, 17, 19 3x17 = 51, 3x19 = 57, 17x19 = 323 3x17x19 = 969
Somme des diviseurs	1 + 3 + 17 + 19 + 51 + 57 + 323 + 969 = 1 440
Formule proposée
Identité du nombre 969	Nombre 969 = 3 x 17 x 19 Diviseurs: 1, 3, 17, 19, 51, 57, 323, 969 Quantité de diviseurs: 8 Somme des diviseurs: 1 440

Somme et quantité

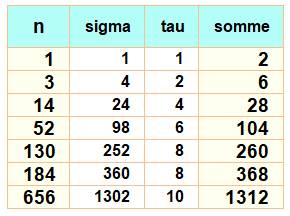
Nombre diédral parfait

Quand la somme des diviseurs ajoutée à leur quantité est égale à deux fois le nombre.

Valeurs

1, 3, 14, 52, 130, 184, 656, 8 648,

12 008, 34 688, 2 118 656, 33 721 216,

40 575 616, 59 376 256, 89 397 016, 99 523 456,

134 438 912, 150 441 856, 173 706 136, 283 417 216,

537 346 048, 1 082 640 256,

6 801 628 304, 91 707 741 184,

14 451 706 793 984, 102 898 828 936 832,

141 573 123 151 232, …

Exemples pour les premières valeurs

Somme et nombre premiers entre eux

Nombre de Duffy

Quand la somme des diviseurs et le nombre composé sont premiers entre eux: aucun facteur commun.

Tous les premiers sont nombres de Duffy.

4, 8, 9, 16, 21, 25, 27, 32, 35, 36, 39, 49, 50, 55, 57, 63, 64, 65, 75, 77, 81, 85, 93, 98, 100, 111, 115, 119, 121, 125, 128, 129, 133, 143, 144, 155, 161, 169, 171, 175, 183, 185, 187, 189, 201, 203, 205, 209, 215, 217, 219, 221, 225, 235, 237, 242, 243, 245, 247, 253, 256, 259, 265, 275, 279, 289, 291, 299, 301, 305, 309, 319, 323, 324, 325, 327, 329, 333, 335, 338, 341, 343, 351, 355, 361, 363, 365, 371, 377, 381, 385, 387, 391, 392, 399, 400, 403, 407, 413, 415, 417, 425, 427, 437, 451, 453, 469, 471, 481, 484, 485, 489, 493, 497, 505, …

2005, 2007, 2015, 2019, 2021, 2023, 2025, 2033, 2035, 2041, 2047, 2048, 2057, 2059, 2061, 2071, 2073, 2075, 2077, …

Voir Nombres et somme de diviseurs

Voyons l'élaboration de la formule générale, pas à pas.

Cas des NOMBRES PREMIERS

Nous savons qu'un nombre premier p

n'est divisible que par 1 et lui-même.

On a vite calculé:

la quantité de diviseurs :

la somme des diviseurs:

(tau) = 2

(sigma) = 1 + p

On adopte la présentation ci-dessous qui va nous permettre de considérer des cas de plus en plus généraux en utilisant une procédure quasi automatique.

Nombre

Quantité

Diviseurs

Somme

Illustration

7 = 1 x 7	= 2	Div. =	1	7
		Somme =	1	+ 7	= 8

Formalisation

p = 1 x p	= 2	Div. =	1	p
		= Somme =			1 + p

Exemples

Nombre	Facteurs	DIVISEURS
Nombre	Facteurs	Quantité	Somme
11 =	1 x 11	2	1 + 11 = 12
13 =	1 x 13	2	1 + 13 = 14
101 =	1 x 101	2	1 + 101 = 102
1 009 =	1 x 1 009	2	1 + 1009 = 1 010

PRODUIT de DEUX FACTEURS PREMIERS

Illustration

6 =	=(1+1)(1+1)	Div =	1	3
2 x 3	= 2		2	6
		Div =	1	1 x 3
			2	2 x 3
		Somme =	3	+ 3 x 3	= 12
		Note	12 = 2 x 6 => Nombre parfait

Formalisation

n =	= (1+1)(1+1)	Div =	1	1 .B
A. B	= 4		A	A .B
		Somme =	1+ A	+ (1+ A) B
		=	(1 + A) (1 + B)

Exemples

Nombre	Facteurs	DIVISEURS
Nombre	Facteurs	Quantité	Somme
10 =	2 x 5	2 x 2 = 4	(1 + 2) (1 + 5) = 3 x 6 = 18
14 =	2 x 7	4	(1 + 2) (1 + 7) = 3 x 8 = 24
15 =	3 x 5	4	(1 + 3) (1 + 5) = 4 x 6 = 24
22 =	2 x 11	4	(1 + 3) (1 + 11) = 4 x 12 = 48

PUISSANCES pures

Illustration

8	= (3 + 1)	Div =	1
= 2³	= 4		2
			4
			8
		Somme =		= 15

Formalisation

n = A^a	= (a+1)	Div =	1
n = A^a	= (a+1)		A
			A²
S_A est une progression géométrique de raison A, d'où cette formule.			A³
		Somme =

Exemples

8 = 2³		=	2⁴ – 1	=	15	=	15
			2 – 1		1

125 = 5³		=	5⁴ – 1	=	624	=	156
			5 – 1		4

PRODUIT DE PUISSANCES

Illustration

200	= (3 + 1) (2 + 1)	Div =	1	5	25
= 2³ . 5²	= 12		2	10	50
			4	20	100
			8	40	200
		Div =	1	1 x5	1 x5²
			2	2 x5	2 x5²
			4	4 x5	4 x5²
			8	8 x5	8 x5²
		Somme =	15	+ 15 x5	+ 15 x5²	= 465

Formalisation

n = A^a . B^b	= (a+1)(b+1)	Div =	1	1 x B	1 x B²
n = A^a . B^b	= (a+1)(b+1)		A	A x B	A x B²
			A²	A² x B	A² x B²
			A³	A³ x B	A³ x B²
		=	S_A	+ S_A . B	+ S_A . B²
S_A et S_Bsont des progressions géométriques de raisons A et B.		= =	S_A ( 1 + B + B² ) S_A . S_B
		=

Exemples

200 = 2³ . 5²		=	2⁴ – 1	x	5³ – 1	=	15 x 124	=	465
			2 – 1		5 – 1		1 x 4

1000 = 2³ . 5³		=	2⁴ – 1	x	5⁴ – 1	=	15 x 624	=	2 340
			2 – 1		5 – 1		1 x 4

THÉORÈME GÉNÉRAL
Nombre & Facteurs	Quantité de diviseurs	Somme des diviseurs
n = A^a . B^b . C^c …	= (a+1)(b+1)(c+1) …

n = A^a . M	= (a+1)M'
n = 2^a . M	= (a+1)M'		divisible par (2^a+1 – 1) un nombre impair

Exemples

Nombre	Facteurs	DIVISEURS
Nombre	Facteurs	Quantité	Somme
10 =	2 x 5	2 x 2 = 4	(2²–1)/(2–1) x (5²–1)/(5–1) = 3 x 6 =	18
11 =	1 x 11	2	1 + 11 =	12
12 =	2² x 3	3 x 2 = 6	(2³–1)/(2–1) x (3²–1)/(3–1) = 7 x 4 =	28
13 =	1 x 13	2	1 + 13 =	14
14 =	2 x 7	2 x 2 = 4	(2²–1)/(2–1) x (7²–1)/(7–1) = 3 x 8 =	24
15 =	3 x 5	2 x 2 = 4	(3²–1)/(3–1) x (5²–1)/(5–1) = 4 x 6 =	24
900 =	2² x 3² x 5²	3 x 3 x 3 = 27	(2³–1)/(2–1) x (3³–1)/(3–1) x (5³–1)/(5–1) = 7 x 13 x 31 =	2 821
3 888 000 =	2⁷ x 3⁵ x 5³	8 x 6 x 4 = 192	(2⁸–1)/(2–1) x (3⁶–1)/(3–1) x (5⁴–1)/(5–1) = 255 x 364 x 156 =	14 479 920

Bilan

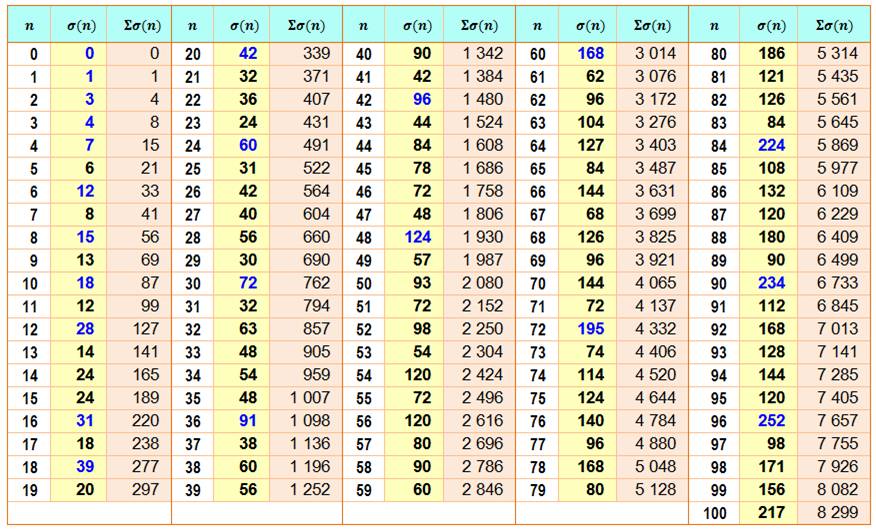
Nous savons désormais calculer la quantité et la somme des diviseurs d'un nombre entier.

Il n'est pas inintéressant de comparer ces valeurs au nombre n lui-même, ne serait-ce que pour bien assimiler ces notions.

Voyons cela >>>

Table des sommes des diviseurs et de leurs cumuls

En bleu les records pour la somme des diviseurs

Même somme pour n et n + 1: 14, 206, 957, 1334, 1364, 1634, 2685, 2974, 4364 … Il sont en nombre infini. Prouvé en 1984 par Heath-Brown.

Même somme pour n et n + 2: 33, 54, 284, 366, 834, 848, 918, 1240, 1504, 2910, 2913, 3304, 4148, 4187, 6110, 6902, 7169, 7912, 9359 … Infinité ? Pas de démonstration à ce jour.

Même somme pour n et n + 3: 382, 8922 …

Même somme pour n et n + 4: 51, 66, 115, 220, 319, 1003, 2585, 4024, 4183, 4195, 5720, 5826, 5959, 8004, 8374 …

Même somme pour n et n + 5: 6, 46, 1030, 2673, 4738, 4785 …

Record de même quantité de diviseurs

1: [1]

12: [6, 11]

24: [14, 15, 23]

72: [30, 46, 51, 55, 71]

168: [60, 78, 92, 123, 143, 167]

240: [114, 135, 158, 177, 203, 209, 239]

336: [132, 140, 182, 188, 195, 249, 287, 299]

360: [120, 174, 184, 190, 267, 295, 319, 323, 359]

504: [204, 220, 224, 246, 284, 286, 334, 415, 451, 503]

576: [210, 282, 310, 322, 345, 357, 382, 385, 497, 517, 527]

720: [264, 270, 280, 354, 376, 406, 418, 435, 459, 478, 537, 623, 649, 667, 719]

Suite >>>

Relation

Pour les nombres pairs, il existe de nombreux cas tels que: sigma(n + k) = sigma(n) + k.

Plus rare avec les nombres impairs:

sigma(2 + 1) = sigma(2) + 1 = 4

sigma(2 + 3) = sigma(2) + 3 = 6

sigma(2 + 5) = sigma(2) + 5 = 8

sigma(74 + 7) = sigma(74) + 7 = 121

sigma(2 + 9) = sigma(2) + 9 = 12

sigma(2 + 11) = sigma(2) + 11 = 14

sigma(4418 + 13) = sigma(4418) + 13 = 6784

sigma(2 + 15) = sigma(2) + 15 = 18

sigma(2 + 17) = sigma(2) + 17 = 20

48 sigma(16 + 17) = sigma(16) + 17 = 48

sigma(6 + 19) = sigma(6) + 19 =31

Nombre et somme des diviseurs avec les mêmes chiffres

[1, 1], [69, 96], [258, 528], [270, 720], [276, 672], [609, 960], [639, 936], [2391, 3192], [2556, 6552], [2931, 3912], [3409, 3904], [3678, 7368], [3679, 3976], [4291, 4912], [5092, 9520], [6937, 7936], [8251, 8512], …

Voir Tables – Index

Fonction diviseur – Généralisation
Définition de la fonction diviseur
k = 0, c'est la quantité de diviseurs
k = 1, c'est la somme des diviseurs
Somme des diviseurs propres ou somme aliquote
k = 2, c'est la somme des carrés des diviseurs
k = 3, c'est la somme des cubes des diviseurs
k = -1, c'est la somme des inverses des diviseurs
Sigma 0 des nombres de1 à 50: 1, 2, 2, 3, 2, 4, 2, 4, 3, 4, 2, 6, 2, 4, 4, 5, 2, 6, 2, 6, 4, 4, 2, 8, 3, 4, 4, 6, 2, 8, 2, 6, 4, 4, 4, 9, 2, 4, 4, 8, 2, 8, 2, 6, 6, 4, 2, 10, 3, 6. Sigma 1 des nombres de1 à 50: 1, 3, 4, 7, 6, 12, 8, 15, 13, 18, 12, 28, 14, 24, 24, 31, 18, 39, 20, 42, 32, 36, 24, 60, 31, 42, 40, 56, 30, 72, 32, 63, 48, 54, 48, 91, 38, 60, 56, 90, 42, 96, 44, 84, 78, 72, 48, 124, 57, 93. Sigma 2 des nombres de1 à 50 (couple en rouge): 1, 5, 10, 21, 26, 50, 50, 85, 91, 130, 122, 210, 170, 250, 260, 341, 290, 455, 362, 546, 500, 610, 530, 850, 651, 850, 820, 1050, 842, 1300, 962, 1365, 1220, 1450, 1300, 1911, 1370, 1810, 1700, 2210, 1682, 2500, 1850, 2562, 2366, 2650, 2210, 3410, 2451, 3255. Couples avec distance 1: (6, 7; S = 50) – Seul (exploration jusqu'à 1 million) Couples avec distance 2: (24, 26; S = 850), (215, 217; S = 48 100), (280, 282; S = 110 500), (1 079, 1 081; S = 1 171 300); (947 516, 957 518; S = 897 826 072 900), … Infinité. Couples avec distance 2: aucun Sigma 3 des nombres de1 à 50: 1, 9, 28, 73, 126, 252, 344, 585, 757, 1134, 1332, 2044, 2198, 3096, 3528, 4681, 4914, 6813, 6860, 9198, 9632, 11988, 12168, 16380, 15751, 19782, 20440, 25112, 24390, 31752, 29792, 37449, 37296, 44226, 43344, 55261, 50654, 61740, 61544, 73710, 68922, 86688, 79508, 97236, 95382, 109512, 103824, 131068, 117993, 141759
Instruction Maple:	Commentaires Exemple avec k = 2. Ouverture des logiciels de théorie des nombres. Calcul d'une séquence de nombres de n = 1 à 5, avec les nombres sigma 2 de n (somme des carrés des diviseurs de n). En bleu, la séquence calculée.

Voir Programmation – Index

Retour Suite	Connaissant la somme des diviseurs, trouver le nombre Diviseurs – Comparaison Diviseurs – Quantités Diviseurs – Tables Facteur le plus grand Somme des carrés des diviseurs – Comparaison Somme des diviseurs et somme des diviseurs du totient Somme des diviseurs et totient –Tables
Voir	Calculs avec les diviseurs Diviseurs Types de nombres selon diviseurs Somme en puissances Théorie des nombres – Index Jeux et puzzles – Index
Site	OEIS A083874 – Numbers n such that sigma(n) + tau(n) = 2n OEIS A003624 – Duffinian numbers: n composite and relatively prime to sigma(n) OEIS A169635 – Integers n such that sigma_2(n) = sigma_2(n + 2) where sigma_2(n) is the sum of squares of divisors of n OEIS A007368 - Smallest k such that sigma(x) = k has exactly n solutions
Cette page	http://villemin.gerard.free.fr/Referenc/Prof/APROF/DivSomme.htm