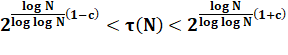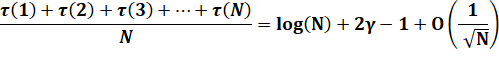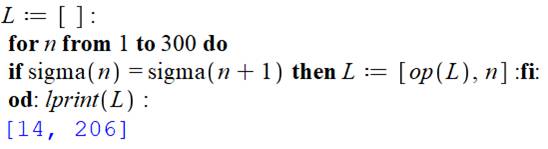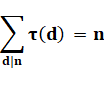|
|||||||||||||||||||||||||||||||||||||||
![]()
|
QUANTITÉ de DIVISEURS Pourquoi ne me l'avait-on pas dit plus tôt ? C'est quasi évident ! et amusant … Je veux voir le résultat tout de
suite. Oups, Par le commencement SVP. En bref, avec un
exemple
|
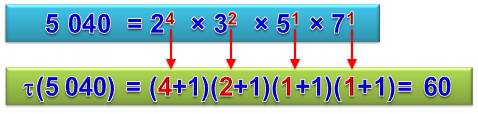
Voir Nombre
hautement composé 5 040
Anglais: how many different factors are there?
|
Propriété Seuls
les carrés
ont un nombre impair de diviseurs. Ex:
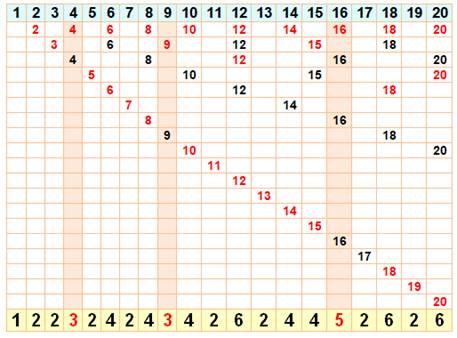
Div(5²) = {1, 5, 25} => quantité de diviseurs = 3. Jeu illustrant la propriété Voir tableau => Aligner
des cartes numérotées de 1 à 20 en
noir au recto et même numéro en rouge au verso. On retourne
une carte sur 2, puis une sur 3, puis une sur 4 puis… une carte sur 20. Seules
les cartes avec un numéro carré se retrouvent en rouge, car retournée u
nombre impair de fois. |
|
Voir Jeux et puzzles
![]()
|
|
||
|
Quantité
de diviseurs |
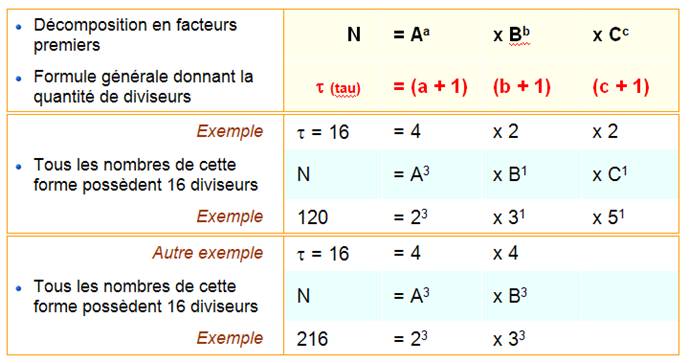
On considère la factorisation
première d'un nombre. La quantité de
diviseurs de ce nombre est égale au produit de ses exposants incrémenté de
un.
|
|
|
Valeur Formule de Wigert |
Plus
précisément:
|
|
|
Moyenne Formule de Dirichlet |
La constante
gamma est la constante
d'Euler. Le terme final est une évaluation de l'écart. Depuis l'évaluation
de cet écart a été raffiné. D'autres évaluations plus sophistiquées existent. |
|
Voir Un
exemple avec factorielle 9
|
|
|
|
Voici les nombres inférieurs à 500 dont la
quantité de diviseurs est égale à 16; il en existe 800 pour les nombres
inférieurs à 10 000.
Le truc avec la quantité de diviseurs:
C'est simplement le produit des exposants des
facteurs du nombre chacun étant augmenté de 1. Cette page explique pourquoi. |
|
Voyons l'élaboration de la formule
générale, pas à pas.
|
|
|||||||||||||||
|
Nous savons qu'un nombre
premier p |
n'est divisible que par 1 et
lui-même. |
||||||||||||||
|
On a vite calculé:
|
1 et p
|
||||||||||||||
|
On adopte la présentation ci-dessous qui va nous permettre de considérer des cas de
plus en plus généraux en utilisant une procédure quasi automatique. |
|||||||||||||||
Illustration
Formalisation
Exemples |
|||||||||||||||
|
PRODUIT de DEUX FACTEURS
PREMIERS |
|
||||||||||||||||||||||||||||||||||||||||||
|
Illustration
Formalisation
Exemples
Remarque Jusque là, compter le nombre de
diviseurs, c'est facile!
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Avec les puissances de nombres
premiers, évidemment, la quantité de diviseurs va dépendre de la puissance
considérée. Illustration
Formalisation
Exemples
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Bilan à ce stade
|
Avec
les puissances de nombres premiers, on trouve la puissance plus 1. |
Aa
|
|
Avec
un produit, osons une hypothèse… c'est peut-être le produit de chaque
puissance plus 1? |
Aa . Bb |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Illustration
Formalisation
Exemples
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||
|
Nombre & Facteurs |
Quantité de diviseurs |
|
|
n = Aa . Bb
. Cc
… |
=
produit des exposants incrémentés |
|
|
n = Aa . M |
divisible
par (a + 1) |
|
Exemples
|
Nombre |
Facteurs |
DIVISEURS |
|
Quantité |
||
|
10 = |
21
x 51 |
2 x 2 = 4 |
|
11 = |
111 |
2 |
|
12 = |
22
x 31 |
3 x 2 = 6 |
|
13 = |
131 |
2 |
|
14 = |
21
x 71 |
2 x 2 = 4 |
|
15 = |
31
x 51 |
2 x 2 = 4 |
|
900 = |
22
x 32 x 52 |
3 x 3 x 3
= 27 |
|
3 888 000
= |
27
x 35 x 53 |
8 x 6 x 4
= 192 |
Bilan
|
OK pour la quantité! Et la somme des
diviseurs? Voyons cela >>> Je souhaiterais m'amuser un peu Curiosité
sur les diviseurs des diviseurs d'un nombre Je veux en savoir davantage: Fonction
arithmétique Note Dirichlet, en 1838, donne une formule
donnant la quantité moyenne de diviseurs des nombres jusqu'à n. Quantité de nombres premiers avec n: Voir Fonction
phi. |
![]()
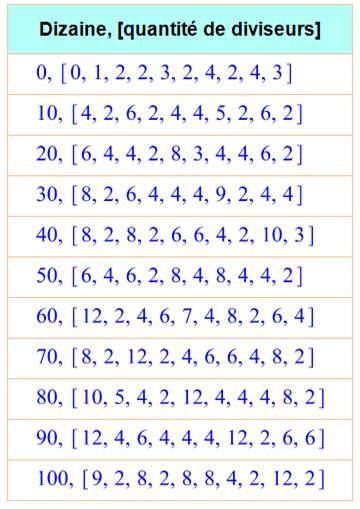
Quantité de diviseurs pour les nombres de 0 à 109
Exemple: 60 a 12 diviseurs et 61 en a 2
seulement.
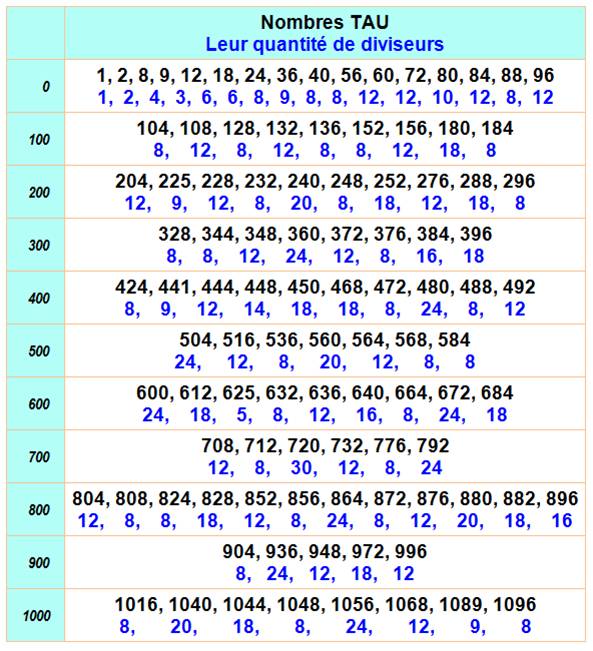
Nombres divisibles par leur quantité de diviseurs
Nombre TAU ou nombre refactorable
Exemple: 104 a 8 diviseurs et 104 est
divisible par 8
Voir
Développement et
programmation / Tables
|
Nombres n et n + 1 ayant la même somme de diviseurs. La programmation Maple est simple:
Liste jusqu'à un million 14, 206, 957, 1334, 1364, 1634, 2685, 2974, 4364,
14841, 18873, 19358, 20145, 24957, 33998, 36566, 42818, 56564, 64665, 74918,
79826, 79833, 84134, 92685, 109214, 111506, 116937, 122073, 138237, 147454,
161001, 162602, 166934, 174717, 190773, 193893, 201597, 230390, 274533,
289454, 347738, 383594, 416577, 422073, 430137, 438993, 440013, 445874, 455373,
484173, 522621, 544334, 605985, 621027, 649154, 655005, 685995, 695313,
739556, 792855, 937425, 949634 |
Voir Sommes avec les mêmes
chiffres
|
|
||
|
Il n'y a
que quatre nombres qui sont égaux à la somme des quantités de diviseurs de
leurs facteurs:
|
1, 3, 18 et 36 18 = 2 x 3 x 3 Diviseurs: 1, 2, 3, 6, 9, 18 Quantité de diviseurs de chacun: 1, 2, 2, 4, 3,
6. 36 = 2x2x3x3 Diviseurs: 1, 2, 3, 4, 6, 9, 12, 18, 36 Quantité de diviseurs de chacun: 1, 2, 2, 3, 4,
3, 6, 6, 9. |
|
|
avec
même quantité de diviseurs |
|
||||||||
|
Nombres de 1 à 250 avec au moins deux
nombres successifs On donne les nombres successifs et
la valeur de tau en queue de liste Ex: 33, 34 et 35 sont trois nombre successifs ayant
quatre diviseurs. 2, 3, 2 14, 15, 4 21, 22, 4 26, 27, 4 33, 34, 35, 4 34, 35, 4 38, 39, 4 44, 45, 6 57, 58, 4 75, 76, 6 85, 86, 87, 4 86, 87, 4 93, 94, 95, 4 94, 95, 4 98, 99, 6 104, 105, 8 116, 117, 6 118, 119, 4 122, 123, 4 133, 134, 4 135, 136, 8 141, 142, 143, 4 142, 143, 4 145, 146, 4 147, 148, 6 158, 159, 4 171, 172, 6 177, 178, 4 189, 190, 8 201, 202, 203, 4 202, 203, 4 205, 206, 4 213, 214, 215, 4 214, 215, 4 217, 218, 219, 4 218, 219, 4 230, 231, 232, 8 231, 232, 8 242, 243, 244, 245, 6 243, 244, 245, 6 244, 245, 6 |
Nombres de 1 à 250 avec au moins trois
nombres successifs 33, 34, 35, 4 85, 86, 87, 4 93, 94, 95, 4 141, 142, 143, 4 201, 202, 203, 4 213, 214, 215, 4 217, 218, 219, 4 230, 231, 232, 8 242, 243, 244, 245, 6 243, 244, 245, 6 301, 302, 303, 4 374, 375, 376, 8 393, 394, 395, 4 445, 446, 447, 4 603, 604, 605, 6 633, 634, 635, 4 663, 664, 665, 8 697, 698, 699, 4 902, 903, 904, 8 921, 922, 923, 4 |
||||||||
|
Nombres de 1 à 100 000 avec quatre
nombres successifs On donne le nombre de tête et tau |
|||||||||
|
242, 6 3655, 8 4503, 8 5943, 8 6853, 8 7256, 8 8392, 8 9367, 8 10983, 8 11605, 8 11606, 8 12565, 8 12855, 8 12856, 8 12872, 8 13255, 8 13782, 8 13783, 8 14312, 8 16133, 8 17095, 8 18469, 8 19045, 8 19142, 8 19143, 8 19940, 12 20165, 8 20965, 8 21368, 8 21494, 8 21495, 8 21512, 8 22855, 8 23989, 8 26885, 8 28135, 8 28374, 8 28375, 8 28376, 8 29605, 8 30583, 8 31735, 8 |
31910, 8 32005, 8 32792, 8 33062, 8 33608, 8 33845, 8 34069, 8 36392, 8 37256, 8 40311, 8 40312, 8 41335, 8 42805, 8 42806, 8 43304, 8 43526, 8 43766, 8 44213, 8 45686, 8 45733, 8 47845, 8 48054, 8 49147, 12 49765, 8 50582, 8 50583, 8 51752, 8 54103, 8 54585, 12 54966, 8 55063, 8 55254, 8 55255, 8 55976, 8 56343, 8 58952, 8 59815, 8 60231, 8 60232, 8 60663, 8 60664, 8 61142, 8 |
62343, 8 65334, 8 66952, 8 67015, 8 68104, 8 69303, 8 71095, 8 73927, 8 74053, 8 76262, 8 76982, 8 77432, 8 78535, 8 78872, 8 79094, 8 79095, 8 79591, 8 80726, 8 82855, 8 84469, 8 86887, 8 87655, 8 87656, 8 87896, 8 90181, 8 90182, 8 90183, 8 91495, 8 93063, 8 94262, 8 94645, 8 95384, 8 95414, 8 95512, 8 95845, 8 95846, 8 97255, 8 98102, 8 98984, 8 99655, 8 99656, 8 |
|||||||
|
Nombres de 1 à 100 000 avec cinq nombres
successifs On donne le nombre de tête et tau 11605, 8 12855, 8 13782, 8 19142, 8 21494, 8 28374, 8 28375, 8 40311, 8 42805, 8 50582, 8 55254, 8 60231, 8 60663, 8 79094, 8 87655, 8 90181, 8 90182, 8 95845, 8 99655, 8 |
|||||||||
|
Nombres de 1 à 1000 000 avec six nombres
successifs On donne le nombre de tête et tau |
|||||||||
|
28374, 8 90181, 8 157493, 8 171893, 8 |
171894, 8 180965, 8 180966, 8 210133, 8 |
298694, 8 346502, 8 369061, 8 376742, 8 |
610310, 8 647381, 8 647382, 8 707286, 8 |
729542, 8 769862, 8 |
|||||
|
|||||||||
Voir Dénombrement de
ces nombres
|
|
||
|
Exemple |
|
|
|
Observations |
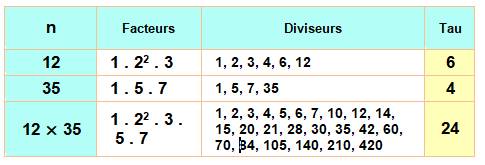
Prenons le nombre 2, un diviseur de 12. Il
devient naturellement un diviseur du produit 12x35. À ce titre, il se combine
à chacun des diviseurs de 35 pour devenir des diviseurs du produit 12x35. Même chose pour les autres diviseurs de 12. On constate bien l'effet multiplicatif
(distributivité des diviseurs de 12 sur ceux de 35).
On remarque que, pour que ça marche, les
diviseurs (donc, les facteurs) doivent être distincts. |
|
|
Quantité de diviseurs
|
On sait que: tout nombre se décompose en facteurs
premiers de manière unique (théorème
fondamental de l'arithmétique): 12 = 2² . 3 La quantité
de diviseurs (tau) est égale au produit des exposants des facteurs
incrémentés de 1. |
|
|
Démonstration: la quantité de diviseurs est une fonction multiplicative |
|
|
|
Soit deux nombres |
a et b tels que (a, b) = 1 (ce qui veut dire que PGCD(a, b) = 1, ou
encore qu'ils sont premiers entre eux. |
|
|
Expressions développées de
ces nombres et de leur produit |
Les ai et bj étant
distincts, aucun regroupement de facteurs possible. |
|
|
Quantité de diviseurs directement déduite des expressions développées
des nombres a, b puis a.b. |
La propriété multiplicative est quasiment
implicite connaissant la formule de calcul de la quantité de diviseurs. |
|
Mêmes chiffres pour n et tau² ou tau3
|
Chiffres identiques pour le nombre et le carré de sa quantité
de diviseurs. Nombre, tau et tau carré [1, 1, 1], [9, 3, 9], [63, 6, 36], [414, 12, 144],
[756, 24, 576], [4320, 48, 2304], [6160, 40, 1600], [6912, 36, 1296], … Nombre, tau et tau cube [1, 1, 1], [46, 4, 64], [152, 8, 512], [261, 6, 216], [1278, 12, 1728], [1287, 12, 1728], [1827, 12, 1728],
[2718, 12, 1728], [2871, 12, 1728], [2916, 21, 9261], [3825, 18,
5832], [3852, 18, 5832], [4690, 16, 4096], [6490, 16, 4096], [7218, 12,
1728], [7821, 12, 1728], [8080, 20, 8000], [8217, 12, 1728], [8325, 18,
5832], [9064, 16, 4096], [9640, 16, 4096], … |
Voir Nombre
1 728
![]()
|
Retour Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/Referenc/Prof/APROF/DivQte.htm
|
![]()