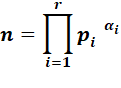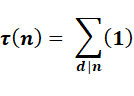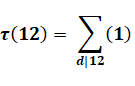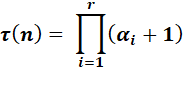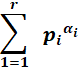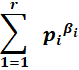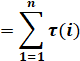|
|||||||||||||||||||||||||||||
![]()
|
Quantité de diviseurs d'un nombre
|
|
|
||
|
Quantité
de diviseurs d'un nombre n: Qui se lit: La
notation "tau" est de Leonard Dickson (1919) |
|
|
|
Exemple
Quantité de diviseurs de n = 12: |
|
|
|
|
||
|
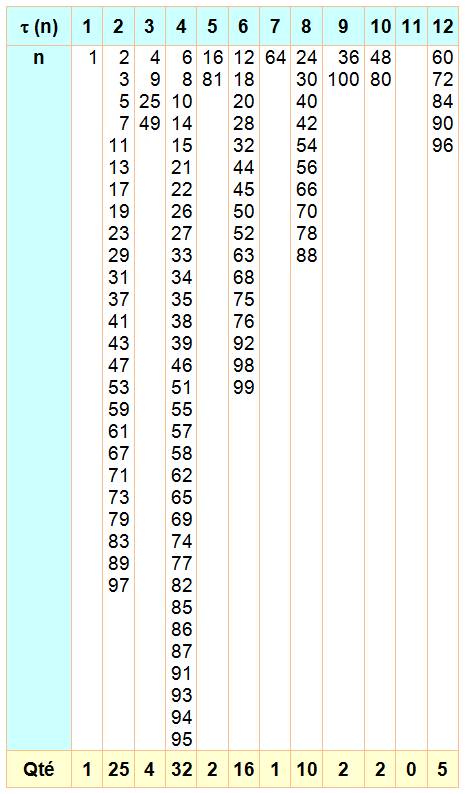
Notez
que la colonne 2 correspond aux 25 nombres
premiers inférieurs à 100. Tout
comme il existe une infinité de nombres premiers, il y a une infinité de
nombre de t(n) donné. Autrement-dit: toutes les colonnes (sauf celle du 1) ont une longueur
infinie. Remarquez
que les colonnes impaires ne comportent que des carrés La
colonne du 2 correspond aux nombres
premiers. |
|
|
Voir Table
des nombres successifs ayant le même tau
|
|
||
|
Formule La définition montre comment
dénombrer en identifiant chacun des diviseurs. Mais, est-il possible de calculer la
quantité par une simple formule? La réponse est "oui". Elle semble un peu compliquée. Mais, tout va s'éclaircir avec un exemple |
|
|
|
Par convention: |
|
|
|
Exemple: n = 12 Il est relativement simple de
trouver la quantité de diviseurs: il suffit d'ajouter 1 à tous les exposants
des facteurs et d'en faire le produit. |
|
|
|
|
|||
|
Le nombre n: |
n = |
|
|
|
Un nombre m du même style Seuls les exposants sont différents. |
m = |
|
|
|
Imposons que m soit un
diviseur de n |
m |
n |
|
|
La condition nécessaire et
suffisante est que chaque facteur de m à sa puissance soit inférieur
ou égal à chacun de ceux de n |
( |
( |
|
|
Ou encore, pour tout i
jusqu'à r |
|
|
|
|
Donc, si m représente un
diviseur de n comment peut-on choisir "bêta
1" |
pour
|
||
|
Poursuivons la démarche pour les
autres "bêta" |
pour
… pour
|
||
|
Face à ces possibilités de choix
exclusifs, le principe
de multiplication peut s'appliquer |
Cumul
des possibilités ( |
||
|
Et, en adoptant notre notation raccourcie |
|
|
|
En cas de difficulté
pour comprendre cette démonstration, voir Familiarisation
Cas particulier
|
Si un nombre possède k facteurs qui ne sont pas
répétés (squarefree) |
|
2k |
|
Exemple avec 24 |
30 = Quantité de facteurs Diviseurs de 3 => Quantité de diviseurs |
2 x 3
x 5 3 1, 2,
3, 5 et 2x3, 2x5, 3x5, 2x3x5 8 = 23 |
Girolamo Cardano dit
Cardan (1537)
|
Ordre: |
|
|
|
|
Borne
évidente |
|
< n |
|
|
Meilleure
approche |
|
< 2 |
|
|
Et
même, pour n > 12 (Isravilov et Allikov - 1980) |
|
< n2/3 |
|
|
Parité: |
|
|
|
|
La
valeur de tau est impaire si n est un carré |
|
= 2k + 1 |
|
|
La
valeur de tau est paire si n n'est pas un carré |
|
= 2k |
|
|
Valeur: |
|
|
|
|
Un
nombre premier possède deux diviseurs |
|
= 2 |
|
|
Quantité
de diviseurs de la puissance d'un nombre premier |
|
= n + 1 = n |
|
|
Il
existe une infinité de nombres tels que: |
|
= a (a>1) |
|
|
Moyenne: |
|
|
|
|
La
valeur moyenne de tau(n) pour
tous les nombres de 1 à n compris (Dirichlet – 1838) Note: g =
0,577… |
|
= ln(n) + 2 |
|
|
Curiosités:
nombres successifs avec
même quantité de diviseurs |
|
||
|
Doublets avec tau identique |
|
|
|
|
Conjecture (Guy): il existe une
infinité de nombres consécutifs ayant le même nombre de diviseurs. |
|
|
|
|
Exemples |
|
= 4 = 4 |
|
|
Triplets |
|
|
|
|
Il
en existe 20 pour n < 1 000 et
ils valent 4, 6 ou 8 Il
en existe 149 pour n < 10 000 et
ils valent 4, 6, 8, 12 ou 16 |
Liste: 33, 85, 93, 141, 201, 213, 217, 230, 242, 243, 301,
374, 393, 445, 603, 633, 663, 697, 902, 921 … |
= 4 = 4 = 4 |
|
|
Quadruplets |
|
|
|
|
Il
en existe 8 pour n < 10 000 et
ils valent 6 ou 8 Il
en existe 125 pour n < 100 000 et
ils valent 8 ou 12 |
|
= 6 = 8 |
|
|
Quintuplets |
|
|
|
|
Il
en existe 19 pour n < 100 000 et
ils valent 8 |
|
= 8 |
|
|
Sextuplets |
|
|
|
|
Il
en existe 18 pour n < 1 000 000 et
ils valent 8 |
|
= 8 |
|
|
Avec 7 et 8 |
|
||
Le premier
de la liste est effectivement le plus petit
Un petit bilan
|
Jusqu'à |
1000 |
10 000 |
100 000 |
106 |
|
Doublets |
|
|
|
|
|
Triplets |
20 |
149 |
1 404 |
|
|
Quadruplets |
1 |
8 |
125 |
|
|
Quintuplets |
0 |
4 |
19 |
|
|
Sextuplets |
|
|
2 |
18 |
Voir Table des nombres successifs ayant même quantité de
diviseurs
|
|
||
|
|
= nombre de diviseurs de n
congruents à m modulo 4 |
|
|
|
n = 5 Diviseurs 1, 5 Mod 4 1, 1 |
|
|
|
n = 100 = 24 . 5² Diviseurs 1, 2, 4, 5, 10, 20, 25, 50, 100 Mod 4 1, 2, 0, 1, 2,
0, 1, 2,
0 |
|
|
|
n = 90 = 2 . 3² . 5 Diviseurs 1, 2, 3, 5, 6, 9, 10, 15, 18, 30,
45, 90 Mod 4 1, 2, 3, 1, 2, 1, 2,
3, 2, 2,
1, 2 |
|
|
|
Diviseurs 1, 2, 3, 5, 6, 9, 10, 15, 18, 25,
30, 45, 50, 75, 90, 150, 225, 450 Mod 4 1, 2, 3, 1, 2, 1, 2,
3, 2, 1,
2, 1, 2,
3, 2, 2,
1, 2 |
|
Voir application en Quantité de sommes de 2 carrés
|
|
|
|
Valeur de tau pour n = 1 à 250 par
rangée de 50
En couleur, les plages
croissantes pour 4 valeurs ou plus de tau. Les records de quantité de
valeurs croissantes s'établissent comme indiqué sur la tableau ci-dessous. |
|
|
n de départ, quantité 2, 3, 13, 4, 241, 6, 12 853, 8, 78 312 721, 11, 125 938 261, 12, |
[les "tau" successifs] [1, 2, 3] [2, 4, 4, 5] [2, 6, 6, 6, 6, 8] [2, 4, 8, 8, 8, 8, 8, 12] [2, 4, 8, 8, 8, 8, 12, 12,
12] [4, 8, 8, 8, 8, 8, 8, 12,
12, 32] [8, 8, 8, 12, 12, 12, 16,
16, 16, 16, 16] [4, 8, 8, 8, 8, 8, 8,
12, 12, 16, 16, 24] |
|
|
|
Programme Maple Réinitialisation et appel aux logiciels de
théorie des nombres. Boucle d'analyse de n et calcul de tau. Si cette valeur est supérieur à la dernière de la
liste L, l'ajouter à la liste Sinon, imprimer la première valeur, la quantité
et la liste des "tau" croissants. Le compteur du record ktm est mis à jour avec la
valeur record. La liste est vidée. En bleu, le résultat du traitement, conforme à ce
qui est indiqué dans le tableau ci-dessus. |
|
Voir Programmation – Index
![]()
|
Suite |
|
|
Retour |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/Referenc/Prof/APROF/FoArDivi.htm
|
![]()