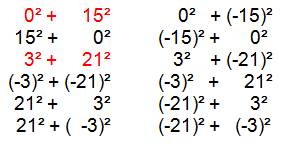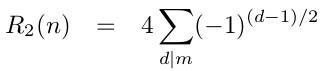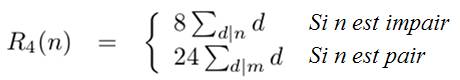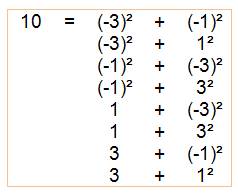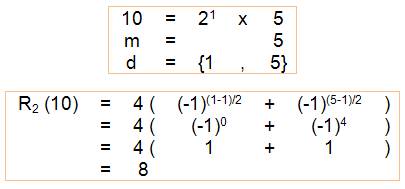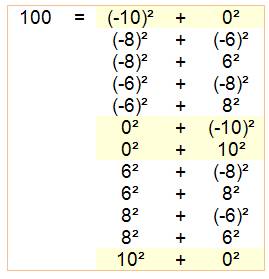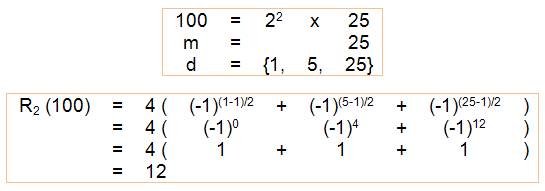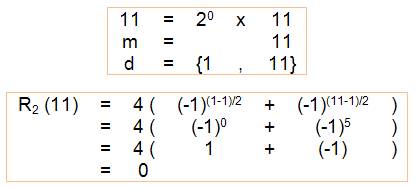|
|||||||||||||||||||||||||||||||
![]()
|
SOMME de DEUX CARRÉS Combien de fois? Quelles
sont les conditions pour qu'un nombre soit
somme de deux
carrés. Alors, combien
de fois l'est-il ? On distingue le cas des nombres premiers et celui des nombres composés. Lorsque le nombre
est composé, on s'intéresse à ses diviseurs. |
|
Cas a² – b²
= c² – d² |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Existe-t-il des cas où la différence de deux
carrés est égale à une autre différence de deux carrés ? Oui, une infinité de possibilités. Même en
supprimant les nombres nuls ou les nombres répétés. Nous allons voir rapidement que cette question est
équivalente à se demander s'il existe des paires de sommes de carrés égales. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Équivalence avec une somme |
a² – b² = c² – d² => a² + d² = c² + b² |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Cas triviaux: a = b et c = d et a = c et b = d |
2² – 2² = 10² – 10² 4² – 3² = 4² – 3² |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Plus petit cas non trivial |
4² – 1² = 8² – 7² |
16 – 1 = 64 – 49 = 15 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Sa version
somme |
4² + 7² = 1² + 8² |
16 + 49 = 1 + 64 = 65 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
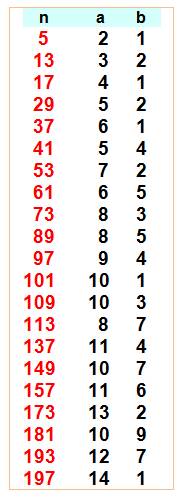
Liste des premiers cas Vingt-six cas de paires de sommes de deux carrés
égales jusqu'à 20 (Tableau). Dit-autrement, en colonne de droite, on a les
nombres qui sont sommes
de deux carrés deux fois avec nombres distincts. Le plus petit nombre est effectivement le nombre
65. En admettant le 0, on a bien sûr: 3² + 4² = 5² +
0². En admettant les nombres répétés, on aurait: 1² +
7² = 5² + 5² = 50. Le théorème
des deux carrés précise les conditions pour qu'un nombre soit somme de
deux carrés. Voir Table Voir Nombres
k fois somme de deux carrés |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
Développement sur la quantité de
sommes de deux carrés
|
|
||
|
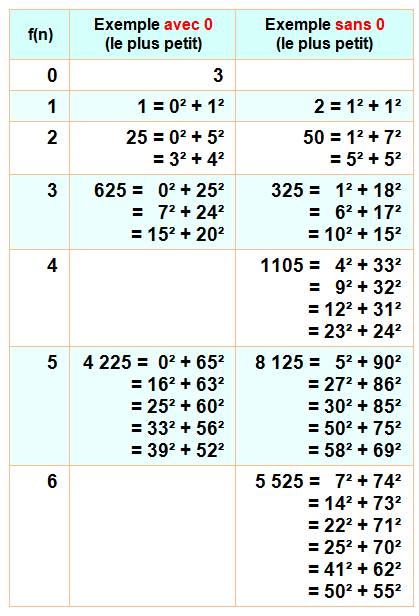
Tous les
nombres ne sont pas somme de 2 carrés. Il y en même une infinité. Et, ceux
qui sont somme de 2 carrés sont également en nombre infini. Parmi eux
certains le sont plusieurs fois. La
fonction f(n) donne la
quantité de représentations d'un nombre en somme de deux carrés. |
|
|
|
|
||
|
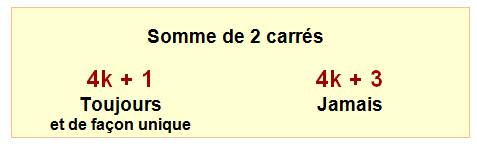
Observations Cherchons toutes les décompositions
en somme de deux carrés des nombres premiers. Les nombres premiers sont tous
de la forme 4k + 1 ou 4 k + 3. Or, nous savons déjà que tous les
nombres en 4k + 3 ne sont jamais somme de 2 carrés. Nous pouvons observer sur la liste
ci-contre que pour tous ceux qui sont en 4k + 1, ils sont bien somme de 2
carrés et ce d'une seule manière. Bilan
|
|
|
|
|
|||
|
Façon de compter F(n) donne
la quantité de représentations d'un nombre en somme de 2 carrés,
Dans ces
conditions
Notation Nombre de diviseurs de n congruents
à m modulo 4 |
F(n) =
f(n) fois toutes les permutations et le signe Exemple: 13 2² + 3²
3²
+ 2² 2² + (-3)² (-3)² + 2² (-2)² + … Total: 8
présentations t(m, n) Voir Tau
modulo |
||
|
Théorème de Jacobi - Il a donné la quantité de sommes pour 4 carrés et aussi pour 6. F(n) est égal à 4 fois la différence entre
les diviseurs égaux à 1 mod 4 et ceux égaux à 3 mod 4 La démonstration dépasse le cadre de ce
site. |
F(n) = 4 ( |
||
|
Exemple 450 = 2 . 3² . 5² t(1, n) = 6 t(3, n) = 3 F(n) = 4
(6 – 3) = 12 Voir Calcul en 450 |
|
||
|
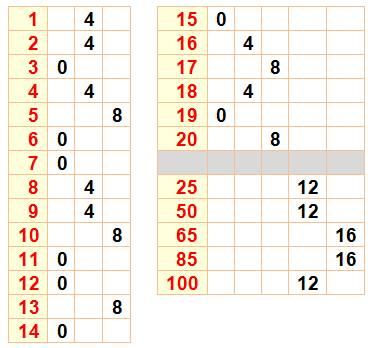
Valeur de F(n) pour les premiers nombres |
|
||
|
|
|
|
On met n sous la forme d'un produit: n = 2a
.m On donne, ci après, les exemples de calculs pour n
= 10, 100 et 11.
D'après Elementary
Methods in Number Theory –
Melvyn B. Nathanson – Springer – 2000 |
|
|
n = 10 |
|
|
Quantité de sommes de deux carrés: 8
Calcul de la somme
|
|
|
n = 100 |
|
|
Quantité de sommes de deux carrés: 12
Calcul de la somme
|
|
|
n = 11 |
|
|
Quantité de sommes de deux carrés: 0 Calcul de la somme
|
|
|
|
||
|
Voir
Constante
Pi |
|
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/Referenc/Prof/APROF/SomCaQte.htm
|
![]()