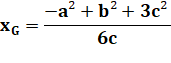Glossaire Médiane

MÉDIANE

Voir Médiane en statistique

«Il y a les plus malins et les moins malins. Le plus malin des moins malins n'est pas beaucoup moins malin que le moins malin des plus malins. » C'est en quelque sorte « la définition de la médiane. »

dit Daniel Justens en citant un album du chat de Philippe Geluck

Daniel Justens a coréalisé “ La mathématique du Chat ” avec Philippe Geluck.

Voir Pensées & humour

Définition

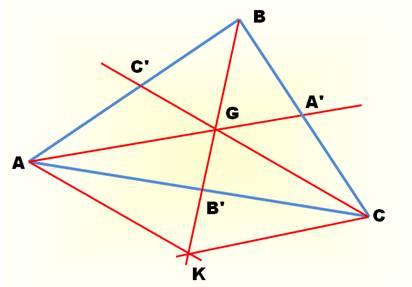
Médianes du triangle: droites passant par un sommet et le milieu du côté opposé; les trois médianes concourent au centre de gravité du triangle.

Médianes du tétraèdre: droites passant par un sommet et le centre de gravité de la face opposée; les trois médianes concourent au centre de gravité du tétraèdre.

Médiane d'un trapèze: droite qui joint les milieux des deux côtés non-parallèles du trapèze. Par extension, la seconde droite qui joint les milieux des deux côtés parallèles.

Médianes d'un polygone: droites qui passent par les milieux de deux côtés non consécutifs.

Médiane d'un trapèze: droite qui joint les milieux des deux côtés non-parallèles du trapèze. Par extension, la seconde droite qui joint les milieux des deux côtés parallèles.

Voir Médiane en statistiques

Propriété fondamentale

AC' = C'B = A'B' AG = 2 GA'

AB' = B'C = A'C' BG = 2 GB'

BA' = A'C = B'C' CG = 2 GC'

Voir Longueur des médianes dans le triangle quelconque

/ Points du triangle

Un petit air sympathique

La médiane découpe le triangle en deux triangles de même aire. Les trois médianes découpent le triangle en six petits triangles de même aire.

Voir Triangle médian

Si le triangle est en métal, il y a autant de matière d'un côté et de l'autre de chaque médiane. Le centre de gravité (G) est quelque part sur chacune de ces médianes. Il est au point d'intersection de celles-ci.

Voir Partage du triangle et centre de gravité

Démonstration

Les médianes sont concourantes

Hypothèses

Un triangle ABC;
AA' et CC' deux médianes qui se coupent en G.

La droite BG coupe AC en B'.

Ce qu'il faut démontrer

AB' = B'C et alors la droite BB' est la troisième médiane.

Toutes les autres Démos/ Proportion 2 : 1

Petit et grand triangles

Traçons les segments joignant les pieds des médianes pour matérialiser le triangle A'B'C'.

Avec l'aide du théorème de Thales, on déduit les propriétés suivantes:

C'A' // AC et C'A' = AB' = B'C

A'B' // AB et A'B' = BC' = C'A

B'C' // BC et B'C' = BA' = A'C

Les triangles ABC (le grand) et A'B'C' (le petit) sont homothétiques de rapport ½.

Parallélogrammes

Notez les trois parallélogrammes:

AC'A'B' et triangle AC'B' = triangle C'B'A' = T_p

On veut dire que les aires des triangles sont égales

BA'B'C' et triangle BA'C' = triangle A'C'B' = T_p

CB'C'A' et triangle CB'C' = triangle B'A'C' = T_p

En opérant une somme des triangles

Triangles (AC'B' + BA'C' + CB'C') = 3 T_p

En y ajoutant le triangle central, on forme le grand triangle:

Aire du grand triangle = 4 x aire du petit triangle.

Médianes

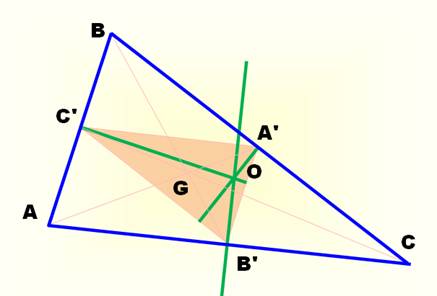
Hauteurs

Médiatrices

Notez également que les médiatrices du grand triangle sont les hauteurs du petit triangle.

On se souvient que AB //A'B', en conséquence, la perpendiculaire à AB (médiatrice de Ab) et aussi la perpendiculaire à A'B'(hauteur de A'B'C' en C').

Les médiatrices étant concourante en un point O, Les hauteurs du triangle A'B'C' le sont aussi; c'est également le cas pour les hauteurs du grand triangle qui lui est homothétique.

Terminologie

Médiane en statistiques: valeur pour laquelle autant d'individus sont en dessous de cette valeur que au-dessus.

Centre de gravité ou centre d'inertie: point d'application de la résultante des actions de la pesanteur sur toutes les parties d'un corps.

Prenons un triangle en tôle; théoriquement il est en équilibre si on place son centre de gravité sur la pointe d'un crayon.

Isobarycentre

Isobarycentre: l'isobarycentre G de trois points (A, B, C) est l'unique point tel que

Où se trouve l'isobarycentre d'un triangle?

On construit le parallélogramme CGBA" de manière à faire apparaître la somme des vecteurs GB et GC (relation de Chasles).

Or cette somme est connue (voir définition ci-dessus)

En comparant les deux égalités

Isobarycentre et centre de gravité

d'un triangle homogène

sont confondus

C'est le point de concours des médianes

Voir Centre de gravité du triangle / Barycentre /

Relation de Chasles / Médianes concourantes – Démonstrations

Propriétés

Les médianes concourent au centre de gravité, en partageant la médiane en 1/3 et 2/3.

Le centre de gravité est le point qui minimise la somme AM² + BM² + CM²

La médiane partage un triangle en deux triangles d'aires égales >>>

Les trois médianes partages le triangles en six triangles de même aire >>>

Théorème des médianes (ou théorème d'Apollonius):

AB² + AC² = 2AA'² + ½ BC²

(trois formules en permutant les sommets)

Autre formulation avec H_A le pied de la hauteur en A

AB² – AC² = 2BC' . H_AA'

(trois formules en permutant les sommets)

Autres Relations avec le centre de gravité

Anglais

Median of a triangle: a line through a vertex of a triangle and the midpoint of the opposite side; the three medians are concurrent at the center of gravity (or center of mass or centroid).

A median of a triangle is the line segment joining a vertex of the triangle to the midpoint of the opposite side

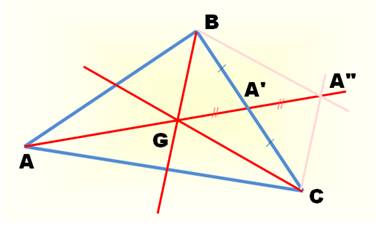
The medians of a triangle. Let ABC be a triangle. Let BB' and CC' be two of its medians, and let them intersect at G. Join AG and produce it to meet BC in C'. It is required to show that AA' is the remaining median of the triangle ABC.

Notez comment on dit "prolonger" en anglais: to produce or to extend.

En savoir plus

Triangles