|
|||||||||||||||||||||||||||||
![]()
|
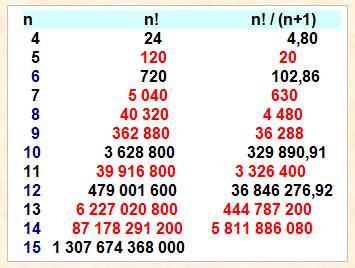
FACTORISATION des FACTORIELLES Méthode de factorisation. En déduire quelques
caractéristiques, comme la quantité de zéros à droite. |
|
|
||||
|
Formons la
factorisation première des nombres factoriels. |
2! = 1 . 2 3! = 1 . 2 .
3 4! = 1 . 2 .
3 . 4 5! = 1 . 2 .
3 . 4 . 5 6! = 1 . 2 .
3 . 4 . 5
. 6 |
= 2 = 6 = 24 = 120 = 720 |
= 2 = 2
. 3 = 23 . 3 = 23 . 3 . 5 = 24 . 32 . 5 |
|
|
Examinons
le cas de 6! Quel est
l'exposant du facteur 2 On
effectue les divisions indiquées Arrêt si
le résultat est inférieur à 1 On prend
les parties entières de ces résultats On les
additionne |
6/2 = 3 6/22 = 1,5 6/23 = 0,75 |
=> 3 => 1 => 0 = 4 |
4 est l'exposant du facteur 2 |
|
|
Même
opération avec 3, le nombre premier immédiatement après 2 |
6/3 = 2 6/32 = 0,66 |
=> 2 => 0 = 2 |
2 est l'exposant du facteur 3 |
|
|
Et avec
le 5, le nombre premier suivant Inutile
d'aller plus loin avec le nombre premier 7, car la division donnera un
résultat inférieur à 1 |
6/5 = 1 6/52 = 0,24 |
=> 1 => 0 = 1 |
1 est l'exposant du facteur 5 |
|
|
|
|
|
Si
n est un nombre entier supérieur ou égal à 1 et si
p est un nombre premier, l'exposant
de p dans la décomposition de n! en facteurs premiers est égal à
Rappel de notation: Les
crochets droits indiquent que l'on retient la partie entière du nombre. Exemple: [5,32] =
5 |
|
|
|
||||
|
Méthode directe |
Application du théorème |
|||
|
10! = 1 . 2
. 3 . 4 . 5 . 6 . 7 .
8 . 9 . 10 = 2 . 3 . 22. 5 . 2.3 . 7 . 23
. 32 . 2.5 = 28 . 34 . 52 . 7 = 3 628 800 |
10/2 = 5 10/22 = 2,5 10/23 = 1,25 |
=> 5 => 2 => 1 = 8 |
28 |
|
|
10/3 = 3,33 10/32 = 1,11 |
=> 3 => 1 = 4 |
34 |
||
|
10/5 = 2 |
=> 2 = 2 |
52 |
||
|
10/7 = 1,42 |
=> 1 |
71 |
||
|
10/11 = 0,9 |
=> 0 |
Fin |
||
|
Cas de 100 ! |
Exemple de calcul pour 2 |
|||
|
100! = 297 . 348 . 524 .
716 .119 . 137 . 175 . 195 .
234 . 293 .
313 . 372 .
412 . 432 .
472 . 53 . 59 . 61 . 67 .
71 . 73 . 79 . 83 . 89 .
97 |
100/2 = 50 100/22 = 25 100/23 = 12,5 100/24 = 6,25 100/25 = 3,12 100/26 = 1,56 100/27 = 0,78 |
=> 50 => 25 => 12 => 6 => 3 => 1 => 0 = 97 |
297 |
|
|
Cas de 1000 ! |
Exemple de calcul pour 5 |
|||
|
1000! => se termine par 249 zéros En effet, la puissance de 5 est 249 et combiné avec 249
fois le 2 (il y beaucoup plus de 2, bien sûr), le produit donne 10 (donc un
zéro) à chaque fois. |
1000/5 = 200 1000/52 = 40 1000/53 = 8 1000/54 = 1,6 |
=> 200 => 40 => 8 => 1 = 249 |
5249 |
|
|
Divisibilité – Théorème |
|
||
|
La factorielle d'un nombre n
est divisible par le nombre immédiatement supérieur, s'il est composé et supérieur à 4. |
|
||
|
n + 1 │ n! Avec n+1 > 4, composé |
|||
|
Exemple: 5! = 120 est divisible par le nombre
composé 6 |
|||
|
Explications |
|
||
|
Avec 5, premier |
(2 . 3 . 4) / 5 |
Impossible. |
|
|
Avec 6 = 2 . 3 |
(2 . 3 . 4. 5) / 6 |
Les facteurs de 6 sont contenus dans la
factorielle. |
|
|
Avec 7, premier |
(2 . 3 . 4 . 5 . 6) / 7 |
Impossible. |
|
|
Avec 8 = 2 . 4 |
(2 . 3 . 4 . 5 . 6 . 7) / 8 |
Un produit de diviseurs donnant 8 est
contenu dans la factorielle. |
|
|
Avec 9 = 3 . 3 |
(2 . 3 . 4 . 5 . 6 . 7 . 8) / 9 |
La factorielle contient 9 dans ses facteurs. |
|
|
Avec n+1 |
Composé |
Il est toujours possible de trouver les
facteurs du nombre composé dans la factorielle. |
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()