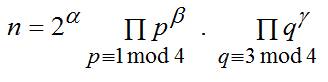|
||||||||||||||||||||||||||||||||||||||||
![]()
|
THÉORÈME FONDAMENTAL de l'ARITHMÉTIQUE
|
Voir Démonstration / Facteurs et diviseurs
|
|
||
|
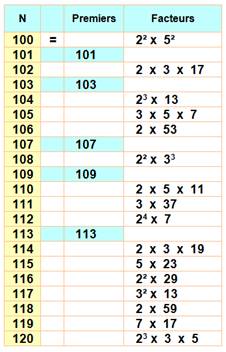
Observons les nombres de 100 à 120
Exemple: 102 = 2 x 51 = 2 x 3 x 17 |
|
|
|
|
||
|
Littéralement Tout
nombre entier naturel N s'écrit de manière unique comme somme de puissances de
10 pour les nombres décimaux, et puissances de B pour toute base B. Alors:
Ce
sont les restes de la division par B
de N, puis des quotients successifs jusqu'à ce que le quotient des
divisions successives soit nul. |
|
|
Voir Numération
/ Formation des nombres
|
|
|||
|
Les
facteurs premiers sont … des nombres premiers Mis
à p Et,
tout nombre premier imp |
p = 2 ou p = {1, 3} mod 4 |
||
|
Fermat a eu l'idée de transformer la forme
canonique sous la forme suivante |
|
||
|
De
sorte qu'il puisse énoncer facilement le théorème suivant: Un
nombre est somme de deux
carrés si et seulement si tous les exposants |
Si tous les alors n est somme
de 2 carrés. |
||
|
Théorèmes |
Tout nombre premier de la forme 4n + 1 est
la somme de deux carrés. Une condition nécessaire pour qu'un nombre
entier soit la somme de deux carrés est que tous ses facteurs premiers soient
de la forme 4n + 1. |
||
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()