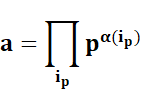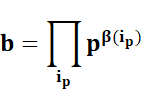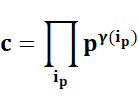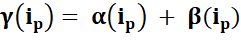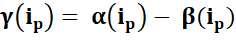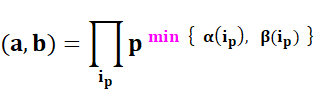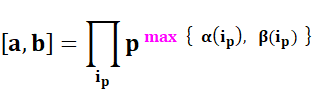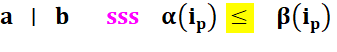|
|||||||||||||||||||||||||||||
![]()
|
THÉORÈME FONDAMENTAL DE
L’ARITHMÉTIQUE PROPRIÉTÉS Quelques propriétés directement
induites par ce théorème. |
|
|
||
|
|
|
|
|
|
|
|
|
Exemples numériques
|
882 = 21 . 32 .
50 . 72 15 = 20 . 31 .
51 . 70 180 = 22 . 32 .
51 . 70 2 381 400 = 23
. 35 . 52 . 72 180 = 22
. 32 . 51 15 = 20 . 31 . 51 12 = 22 . 31 . 50 |
|
|
|
||
|
|
|
|
|
Exemples numériques |
120 = 23 . 31
. 51 180 = 22 . 32
. 51 (15, 180) = 22
. 31 . 51 = 60 120 = 23 . 31
. 51 180 = 22 . 32
. 51 [15, 180] = 23
. 32 . 51 = 360 |
|
|
|
||
|
|
|
|
|
Exemples numériques |
Divisible 180 = 22 . 32 . 51 15
= 20 . 31 . 51 Non divisible 180 = 22
. 32 . 51 120
= 23 . 31 . 51 |
|
|
|
|||
|
|
n = a² |
25 = 5² |
|
|
|
n = |
19
600 = 24 . 30 . 52
. 72 = 140² |
|
|
|
n = |
100
000 = 25 . 30 . 55 . 70 = (2 . 5)5 |
|
Voir Nombres carrés
|
|
|||
|
|
nS = Avec |
6 = 2 .
3 105 =
3 . 5 . 7 3 289 = 11 . 13 . 23 |
|
|
Square-free numbers We say that a
is square-free if 1 is the
largest square dividing a. Thus a
is square-free if and only if the exponents |
|||
|
|
1,
2, 3, 5, 6, 7, 10, 11, 13, 14, 15, 17, 18, 19, 21 … |
||
|
|
n = a² . ns |
12 = 2². 3 13 = 1 . 13 14 = 1 . 14 60 = 2². 15 |
|
Voir Nombres
sans facteur carré / Nom des nombres / Nombres simples / Nombres homogènes
|
Nombres
plénipotents ou puissants (powerful numbers or squarefull
numbers) |
|
||
|
Nombres qui n'a pas d'exposant inférieur à 2. Le produit de nombres plénipotents est aussi un
plénipotent. |
nS = Avec |
108 =
22 . 33 10 575 =
32 . 52
. 72 136
125 = 32 . 53 . 112 |
|
|
Un nombre n est plénipotent si, pour tout nombre
premier p qui divise n, son carré p² divise aussi n. |
Si pour tout p Nous avons p² Alors n est plénipotent |
2
et 3 sont les facteurs premiers de 108 22
│108 32
│108 108
est plénipotent |
|
|
Powerful numbers A positive integer N is called powerful if p²
│N whenever p │N.
An integer N is powerful if and only if N
can be expressed in the form N = m2 . n3 |
|||
|
|
4,
8, 9, 16, 25, 27, 32, 36, 49, 64, 72, 81, 100, 108, 121, 125, 128, 144 … |
||
|
Heath-Brown a montré en 1988 que
tout nombre naturel suffisamment grand est la somme d'au plus trois nombres
puissants. Le plus grand nombre qui n’est pas la somme de trois nombres
puissants est probablement 119. |
118 = 32
+ 32 + 10² = 33 + 33 + 26 119 = / 120 = 22 + 23 + 22∙33
= 22 + 24 + 102 = 22 + 25 + 23∙32 … |
||
|
Partition
en somme de deux nombres puissants distincts. |
Même autour de 100 000, il existe
des trous. |
99
997 = 53∙112 + 23∙1032 99
998 = / 99
999 = / 100
000 = 122 + 24∙792 |
|
|
Tout nombre plénipotent est le produit d'un carré et
d'un cube. |
N = m2 .
n3 |
63
504 000 = 27 . 34 . 53 . 72 =
(24 . 34 . 50 . 72) ( 23
. 30 . 53 . 70) =
(22 . 32 . 7)2 ( 2 . 5)3 =
(22 . 32 . 7)2 ( 2 . 5)3 = 2522 . 103 |
|
Voir Nombres 2-puissants et 3-puissants
/ Nombres
puissants au bac / Table
/
Nom des nombres / Nombres plénipotents / Nombres riches
|
|
|
|
Liste: 72, 108, 200, 288,
392, 432, 500, 648, 675, 800, 864, 968, 972, 1125, 1152, 1323, 1352, 1372,
1568, 1800, 1944, 2000, 2312, 2592, 2700, 2888, 3087, 3200, 3267, 3456, 3528,
3872, 3888, 4000, 4232, 4500, 4563, 4608, 5000 ... |
|
Voir Nombres
d’Achille – Développements
|
|
|||
|
|
n = 2k . m Avec m impair et
k |
3 = 20 . 3 176 = 24 . 11 1
936 = 24 . 121 3
360 = 25 . 105 |
|
|
|
n = a . b Avec a simple Et
b = x² |
20
580 = 22 . 3 . 5 . 73 =
105 . 14² |
|
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()