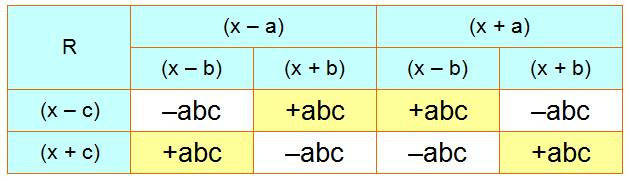NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 10/09/2023 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	ÉQUATIONS
Débutants Équations	Troisième degré				Glossaire Équations
INDEX Équations	Théorie	Exemple 1	Méthode	Historique
	Factorisation	Exemple 2	Exemple 3	Symétrie
	Nombre d'argent	Système (3 équa.)
		Sommaire de cette page >>> Forme générale >>> Exemples de résolution rapide >>> Signe >>> Première série – À l'envers >>> Deuxième série – À l'endroit >>> Troisième série – Dégénéré >>> Quatrième série – Identités >>> Tables de polynôme du 3^e degré

Polynôme du troisième degré

Factorisation

Familiarisation et résolution des équations SIMPLES du troisième degré.

Avant de vous lancer dans les calculs longs et fastidieux de résolution de telles équations, vérifiez qu'il n'y a pas une racine évidente. Dans l'équation, le terme constant est riche de renseignements sur les racines du polynôme.

Forme générale
La constante R est égale au produit des trois racines: R = – abc. Le coefficient P est égal à leur somme: P = – (a + b+ c). Remarques mises à profit pour résoudre rapidement certaines équations.

Exemples de résolutions immédiates

Résolution possible si les racines sont entières et petites. Une vérification ultime consiste à remplacer x par sa valeur dans le polynôme initial. Par exemple, pour x = 1 => 1 – 6 + 11 – 6 = 0. Dans ce cas pour atteindre la somme 5, nous avons dû doubler l'un des diviseurs. Ce troisième exemple montre l'intérêt de la vérification: pour s'assurer que le choix des racines est bon et que les signes sont bien attribués.

Voir Tables de ce type d'équations / Diviseurs et facteurs

Histoire de signe
Quel est le signe de R selon les signes des racines? R est positif si les trois facteurs sont en + ou si un seul est en +. R est négatif si les trois facteurs sont en – ou si un seul est en –. Les racines ont le signe inverse des signes dans la factorisation.

Exemples détaillées

Première série – À l'envers
Observons le produit de trois facteurs. Pour a = 1 ou 2 ou 3, le polynôme est égal à 0. Ces trois nombres sont les racines de l'équation proposée. Je remarque que la constante 6 est bien le produit de 1, 2 et 3 Les trois facteurs accompagnés du signe moins engendrent bien une constante R négative (–6).	(x – 1) (x – 2) (x – 3) = 0 x^3 – 6x^2 + 11x – 6 = 0 Racines: {1, 2, 3} 1 – 6 + 11 – 6 = 0 8 – 24 + 22 – 6 = 0 27 – 54 + 33 – 6 = 0
La factorisation avec trois signes positifs engendre bien une constante R positive. R est bien le produit de 1 x 2 x 3 Les racines, de signe opposé à ceux de la factorisation, sont toutes les trois négatives.	(x + 1) (x + 2) (x + 3) = 0 x^3 + 6x^2 + 11x + 6 = 0 Racines: {–1, –2, –3} 1 – 6 + 11 – 6 = 0 8 – 24 + 22 – 6 = 0 27 – 54 + 33 – 6 = 0

Deuxième série – À l'endroit
Avec une telle équation, je suspecte des racines en: {1, 12, 12}, aux signes près. Le coefficient de x^2, somme des racines, étant unitaire, je confirme que la configuration –1, –12 et +12 doit convenir.	x^3 – x^2 – 144x + 144 = 0 12^3 – 12^2 – 144 x 12 + 144 = 0 (–12)^3 – (–12)^2 – 114 (–12) + 144 = –12^3 – 12^2 + 12^3 + 12^2 = 0 1 – 1 – 144 + 144 = 0 (x – 1) (x – 12) (x + 12) = 0
Avec 144, j'ai sans doute à faire aux mêmes racines {1, 12, 12}. 144 est négatif: un facteur ou les trois sont négatifs La somme, coefficient de x^2 est égale à 23. C'est la somme: 12 + 12 – 1. Les racines sont: {+1, –12, –12}	x^3 + 23x^2 – 120x – 144 = 0 (x – 1) (x + 12) (x + 12) = 0

Troisième série – Dégénéré
Factorisation immédiate avec x. Puis, reconnaissance d'une identité remarquable. Les racines sont évidentes	x^3 – x = 0 x (x^2 – 1) = 0 x (x – 1) (x + 1) = 0 Racines: {–1, 0, + 1}
Factorisation immédiate avec x. Les racines sont celles vues ci-dessus, plus le 0.	x^4 – 6x^3 + 11x^2 – 6x = 0 x (x^3 – 6x^2 + 11x – 6) = 0

Quatrième série – Identités
La constante 4 indique que le produit est susceptible d'être 1 x 2 x 2. Soit la présence d'un carré en x – 2. Je tente de rassembler des termes en carré parfait (identité remarquable). Il suffit de calculer ... Racines: {1, 2, 2}, une racine double.	x^3 – 5x^2 + 8x – 4 = 0 x^3 – 5x^2 + 8x – 4 = 0 (x – 2)^2 = x^2 – 4x + 4 x^3 – 4x^2 + 4x – x^2 + 4 x – 4 = 0 x^3 – 4x^2 + 4x – x^2 + 4 x – 4 = 0 x (x – 2)^2 – (x – 2)^2 = 0 (x – 1) (x – 2)^2 = 0
Avec notre habitude, nous savons que les racines seront en 1,2, 2. Mais essayons autre chose: une factorisation partielle en prenant un terme sur deux. Factorisation et développement immédiat. Racines: {1, 2, –2}	x^3 – x^2 – 4x + 4 = 0 x^3 – 4x – x^2 + 4 = 0 x(x^2 – 4) – (x^2 – 4) = 0 (x – 1) (x^2 – 4) = 0 (x – 1) (x – 2) (x + 2) = 0
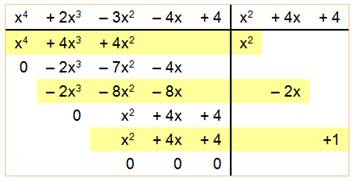
En remplaçant x par 1, nous vérifions que 1 est bien racine. c'est le cas aussi pour –1. La 4 final suggère que 2 est une racine double. Avec +2, le polynôme vaut 16. Avec –2, il vaut 0. J'essaie ces valeurs! Si j'ai un doute, ou un cas plus difficile, osez la division. Avec –2 comme solution double, je prends (x + 2)^2 = x^2 + 4x + 4x Division du polynôme initial par celui-ci	x^4 + 2x^3 – 3x^2 – 4x + 4 = 0 (x + 1) (x – 1) (x + 2) (x + 2) = x^4 + 4x^3 + 3x^2 – 4x – 4 NON (x + 1) (x + 1) (x + 2) (x + 2) = x^4 + 6x^3 + 13x^2 + 12x + 4 NON (x – 1) (x – 1) (x + 2) (x + 2) = x^4 + 2x^3 – 3x^2 – 4x + 4 OUI = (x – 1)^2 (x + 2)^2

TABLES

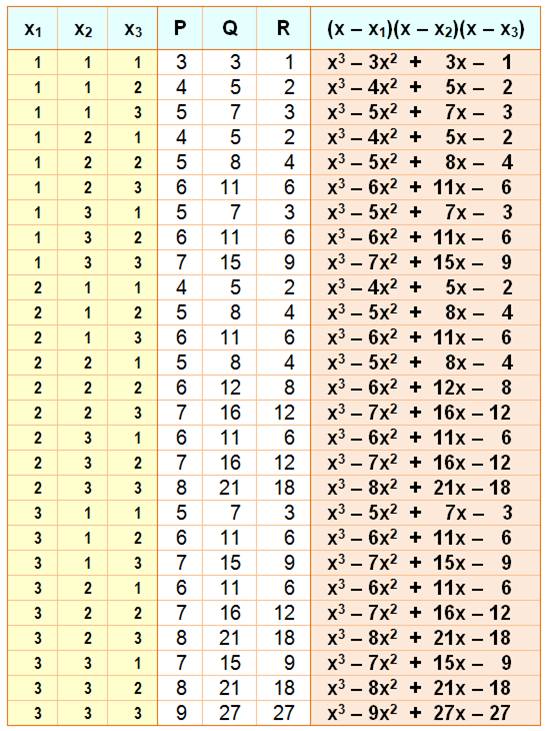
Racines positives de 1 à 3 pour chacune

P = somme, Q = somme des produits deux à deux et R = produit

Observez que les coefficients sont –P, Q et –R

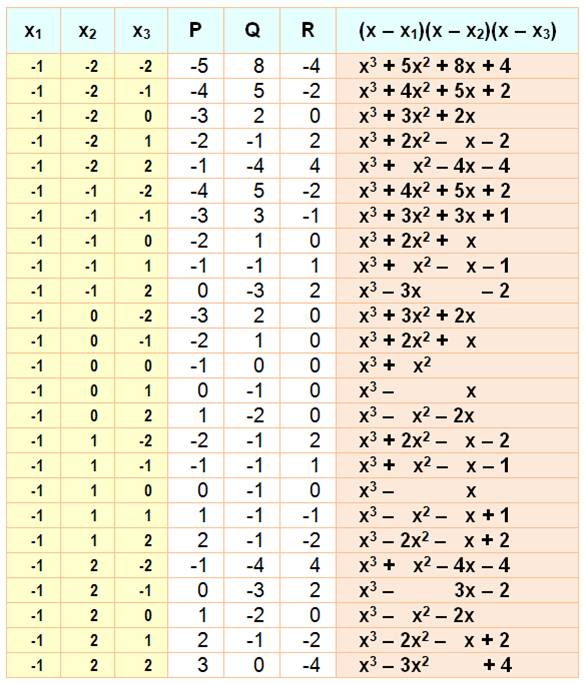
Racines positives et négatives:

x1 = {-1, 0, 1}; x2 = {–2 à +2}; x3 = {–2 à +2};

Observez que les coefficients sont également P, Q et R, mais attention aux signes

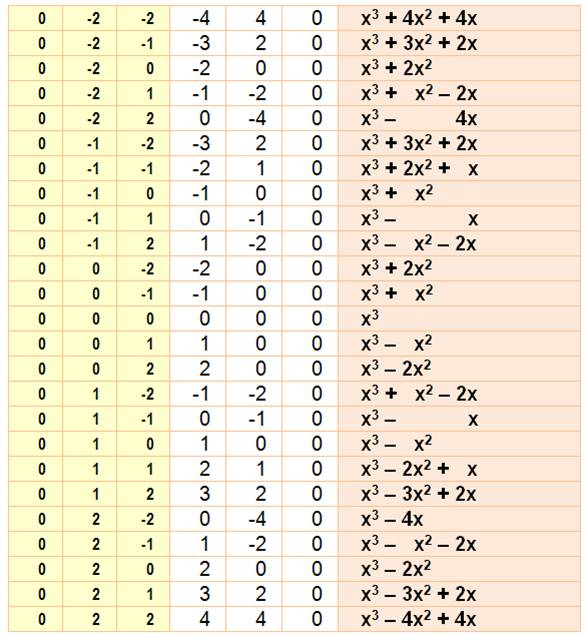
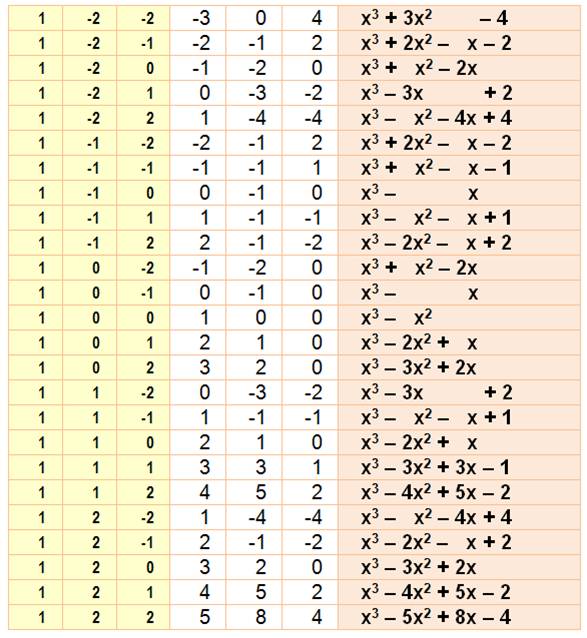
Voir Tables

Suite	Résolution des équations du 3^e degré Système d'équations avec troisième degré – Énigme
Voir	Algorithme d'Héron Équation - Glossaire Équation de Pell Méthode de Newton Système d'équations particulier
Cette page	http://villemin.gerard.free.fr/ThNbDemo/Eqa3dFac.htm