|
||||||||||||||||||||||||||||
![]()
|
Théorème
de Fermat-Wiles avec n = 3 Primitif
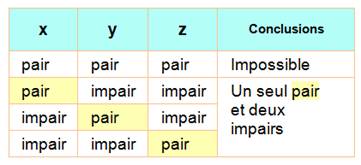
/ Pair et impair Nous nous intéressons aux triplets primitifs. Les nombres deux à deux sont premiers entre eux. L'un des trois est pair et les deux autres impairs. |
|
|
||
|
Premiers entre
eux Les
nombres entiers x, y et z sont premiers
entre eux, ce qui veut dire qu'ils le sont deux par deux. |
(x,
y) = 1 Forme abrégée de PGCD(x, y) = 1 (x,
z) = 1 (y,
z) = 1. |
|
|
Si
un couple n'était pas premier, le facteur commun se retrouverait évidemment
dans le troisième comme résultat du calcul. |
Si, par
exemple: x
= 2X et y = 2Y, alors (2X)3 + (2Y)3 = 8X3 + 8Y3
= z3 et z l'est par 2. |
|
|
|
||
|
Nous
venons de montrer de facto que x et y ne peuvent pas être tous deux pairs
sinon le troisième est lui aussi pair et ces nombres ne seraient pas premiers
entre eux. |
Nous
allons montrer que: x
et y sont de parités opposées. |
|
|
Si
l'un est pair et l'autre impair: |
x
= 2X et y = (2Y+1), alors (2X)3 +
(2Y+1)3 = 8X3 + 8Y3 +
12Y2 + 6Y + 1
|
|
|
Si
les deux sont impairs: |
x
= (2X+1) et y = (2Y+1), alors (2X+1)3
+ (2Y+1)3 =
8X3 + 8Y3 +12X2 + 12Y2 + 6Y+ 2 Tous
les termes sont pairs |
|
|
Bilan: |
|
|
|
L'un
des trois est pair. Avec l'écriture proposée, on constate qu'il suffit d'inverser
les rôles de x avec z ou y avec z pour que z soit toujours pair. |
x3
+ y3 = z3 x3
+ y3 – z3 = 0 x3
+ y3 + (–z)3 = 0 On
choisit z pair Alors x et y sont impairs. |
|
![]()
|
Retour |
|
|
ou Suite |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Addition/FERMAT/Fer3Prim.htm |
![]()