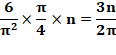|
Édition du: 15/01/2024 |
|
INDEX |
Théorème de Pythagore |
|||
![]()
|
TRIPLETS de Pythagore Approximation de π Comment la constante Pi se retrouve dans les triplets
de Pythagore ? Il existe un rapprochement entre: a² + b² = c² et sin² + cos² = 1 lequel permet d'inscrire les
triplets sur la circonférence du cercle
unité. |
||
|
|
Sommaire de cette page >>> Cercles
inscrits et triplets >>>
Cercle unité >>>
Quantité de triplets et Pi |
Débutants Glossaire |
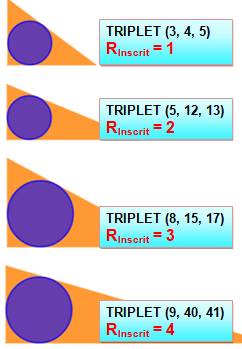
Disque et
couronne avec le triplet (3, 4, 5)
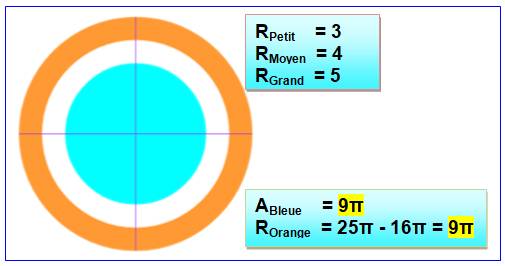
|
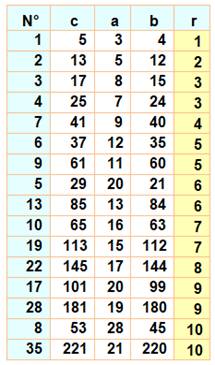
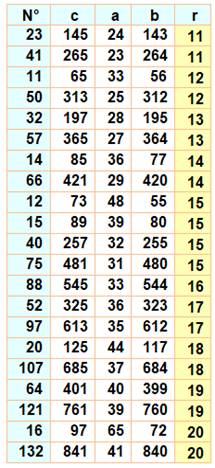
Table des triplets avec rayon du cercle inscrit de 1 à 20 Le
rayon
du cercle inscrit se calcule aisément:
|
Voir Triplet isiaque (3, 4, 5) |
|
|
|
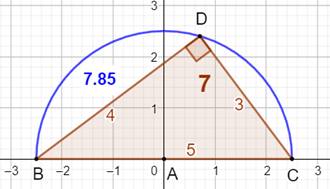
Approche Avec
le triplet (3, 4, 5), dessiner un demi-cercle de diamètre c = 5. Positionner
le point D sur le cercle
à la distance 4 du point B. Il sera automatiquement à la distance 3 du point
C. L'angle en D est naturellement
droit et le triangle BCD est bine rectangle. Observation pour a et b Comparons
les longueurs:
La
longueur des deux cordes est proche (inférieure) de celle du demi-cercle. |
La
longueur des deux cordes (7) est une approximation par défaut du périmètre du
demi-cercle (7,85…). Selon
la position du point D, cette longueur varie de 5 à 5√2 = 7,07… Encore loin de 7, 85 ! |
|
|
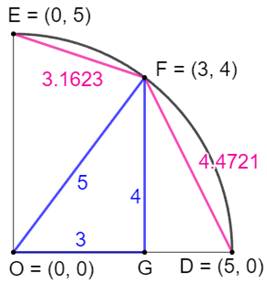
Une meilleure approximation Un
quart de cercle de rayon c = 5 cm. Le
point F de coordonnées (3, 4) pour former le triangle rectangle OFG (3, 4, 5). On
calcule la longueur des cordes EF et DF;
|
|
|
|
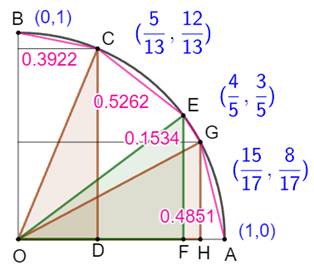
Une meilleure approximation On
normalise le rayon du quart de cercle à 1. On
place le triplet (3, 4, 5) qui devient (3/5, 4/5, 1). On
ajoute les deux triplets suivants. On
calcule BCEGA.
|
|
|
|
En
normalisant les triplets de sorte que c = 1, soit le nouveau triplet: (a/c, b/c, 1), alors chaque triplet est
représenté par un point de coordonnées rationnelles
(a/c, b/c), sur la circonférence du
cercle unité. En
positionnant tous ces triplets, la circonférence du cercle sera émaillée de
points rationnels, dont la réunion formera une ligne brisée proche par défaut
du demi-cercle. Ligne brisée infinie,
mais pas
continue. |
|
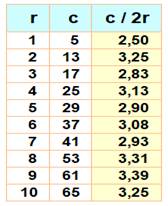
Observation On
liste les triplets primitifs successifs en notant leur rang. On
divise la valeur de l'hypoténuse c par deux fois le rang.
Le ratio oscille autour de la valeur de Pi. |
Voir Graphes à
la demande |
||
|
Explication Le
fait
fondamental prouvé par Lehmer en 1900 est que: La quantité
(asymptotique) de triplets primitifs < n est Q = n / 2Pi. Par exemple pour
n= 1000, on a 1000 / (2 × 3,14…)
= 159,15 et le triplet n° 159 est tel que c = 1009.
Note: avec a = 559 et b = 840. De
sorte que si on calcule pour chaque triplet: r = c / 2Q On
obtient toujours un nombre proche
de π. Exemple: avec
le 4e triplet (25, 7, 24), on a: Comme,
le théorème de Lehmer est valable asymptotiquement, il est normal d'observer
que le ratio oscille autour de π, surtout pour les petits nombres. |
Une idée de la démo La
démonstration du théorème n'est pas simple. Un
des arguments, introduisant le nombre Pi, est de limiter le choix aux
triplets primitifs. Parmi
deux nombres pris au hasard la probabilité qu'ils premiers entre eux est
égale à 6 / Pi². Le
second argument est celui-ci: La
quantité de paires a² + b² < n est de l'ordre de Pi . n / 4. Le
produit des deux est égal à: Reste
à traiter le coefficient 3/2 avec des considérations de parité liées à la
propriété des triplets. |
||
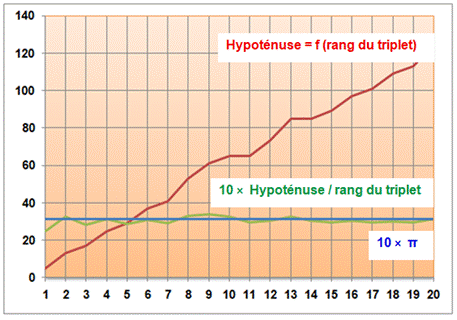
Graphe
montrant l'écart du ratio par rapport à l'unité pour n de 0 à 900
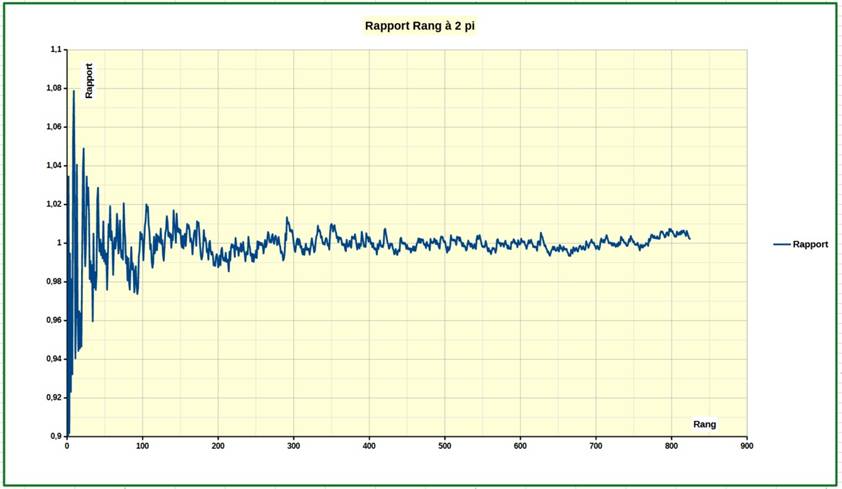
Merci à Gérard Baillet pour l'idée de cette page et pour
ses informations dont le graphique ci-dessus
![]()
|
Retour |
|
|
|
Suite |
|
|
|
Applications
du théorème |
|
|
|
Voir |
|
|
|
Sites |
|
|
|
Cette
page |
http://villemin.gerard.free.fr/Wwwgvmm/Addition/ThPythPi.htm
|
|
![]()
![]()