|
|||||||||||||||||||||||||||||||||
![]()
|
Carrés magiques Tour de magie Je devine la somme Tour de magie par
sélection de nombres dans un carré magique. Je
suis capable de deviner la somme des nombres qui restent. |
|
|
||
|
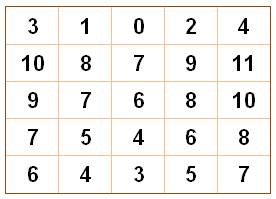
Avec ce
carré, tu proposes un tour de magie. Tu
demandes à un ami de choisir un des nombre du carré magique. Tu barres tous
les nombres de la même ligne et de la même colonne. Tu
demandes de choisir un autre nombre parmi ceux qui restent. Tu barres les
autres de la même ligne et la même colonne. Tu
recommences jusqu'à ce qu'il ne reste plus de nombres. |
|
|
|
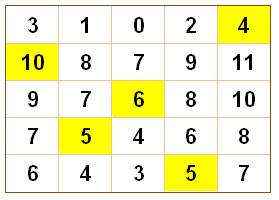
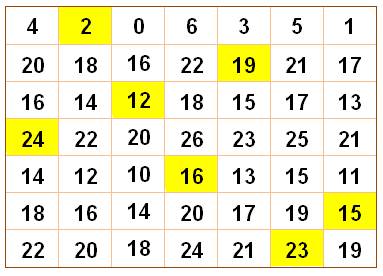
Le carré
montre en jaune un exemple des cinq nombres choisis. Tu calcules
la somme: 10 + 5 + 6 + 5 + 4 = 30 Tu paries
que si on recommence, ton carré est si magique que la somme sera la même.
C'est une somme magique cachée dans le
carré. |
|
|
|
|
||
|
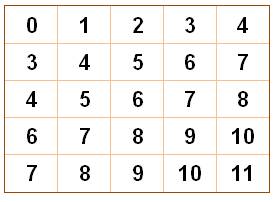
Le carré
magique en question est un cousin de celui-ci. Il a été "mélangé"
en inversant des lignes et des colonnes pour ne pas montrer cette structure
très simple. Quelle
est cette structure?
Les deux
sommes ajoutées donnent 10 + 20 = 30, le nombre
magique. |
Carré original simple. Le carré magique ci-dessus est obtenu en
permutant des lignes et des colonnes pour cacher la simplicité de la
construction. |
|
|
|
||
|
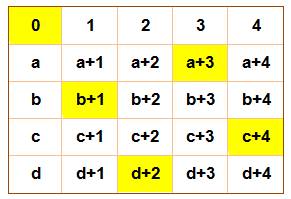
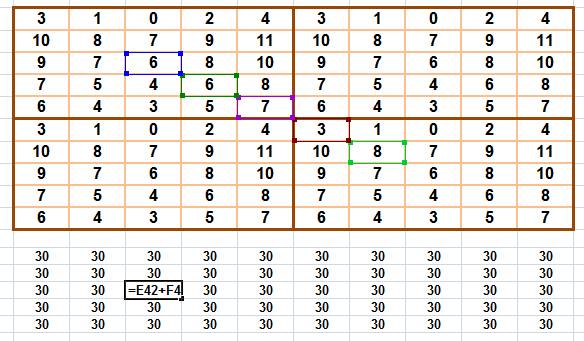
Le
tableau générique se présente comme indiqué à droite. On
remarque que: 0 + 1 + 2 + 3 + 4 + a + b + c + d = SM (la somme magique, 30
pour le tour ci-dessus). On a bien un nombre de chaque. Le tour
de magie revient à choisir un nombre dans chaque ligne et dans chaque
colonne. Chaque nombre est la somme de deux termes:
|
Les nombres a, b, c et d sont répartis sur chacune des lignes; de
même, les nombres 1, 2, 3, 4 sont répartis sur chaque colonne. Ici en jaune, en ligne nous avons: 0, 3, 1, 4, 2; et en colonne 0, b,
d, a , c. Ils sont tous là et une seule fois. leur somme est la somme
magique. |
|
|
|
|
|
Il se
trouve que de tels carrés adaptés à ce tour de magie sont pandiagonaux. Toutes
les diagonales montantes et descendantes de ce tapis (quatre fois le carré originel)
produisent la somme magique. L'une d'elle est mise en évidence pour montrer la
structure du calcul sur tableur.
Diagonales
descendantes et diagonales montantes |
|
|
|
||
|
Degrés de liberté Vous
pouvez réaliser la somme SM que vous voulez! Connaissant
le truc, vous pouvez faire des carrés de la taille que vous voulez. |
Avec la ligne 0, 1, 2, 3, 4 de somme
10 Le choix
de a, b, c, d est vaste, il suffit que leur somme fasse SM – 10. Par
exemple: SM = 28, alors a + b + c + d = 18; une possibilité: a = 3, b = 4; c
= 5; d = 6. Avec autre somme sur la ligne Vous
pouvez choisir une autre somme. Par exemple 13, avec 0, 1, 3, 4, 5. Attention:
si les nombres ne sont consécutifs, la construction est plus délicate. La somme
a + b + c+ d sera alors: SM – 13. |
|
|
Somme magique: 111 = 21 + 90 |
||
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/CarreMag/aaaCMag/CarMaDev.htm
|
![]()