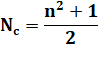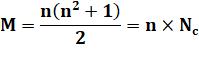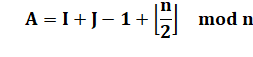NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 13/05/2020 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Carrés magiques
Débutants Carrés magiques	Carré magique 5 x 5				Glossaire Carrés magiques
INDEX Carrés magiques Jeux	Carré 5 x 5	Construction	Diaboliques	Générique
	Propriétés	Premiers	Pheru
		Sommaire de cette page >>> Caractérisation >>> Construction avec le cavalier >>> Principe de l'enroulement >>> Construction géométrique >>> Construction par addition de deux carrés latins >>> Bilan sur les règes de construction – Carrés magique associatif d'ordre impair >>> Anglais

Voir approche en Observation sur carré d'ordre 3 / Truc de B. Franklin

Carré magique d'ordre impair – Caractérisation
Ordre	n	5
Dernier nombre	Nn,n = n²	25
Nombre central		13
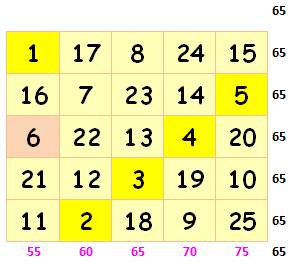
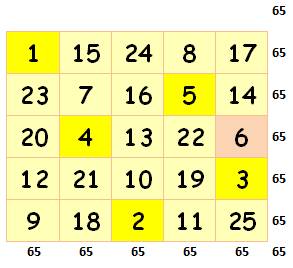
Somme magique		65
Nombre en rangée I et colonne J Rappel: les deux crochets bas signifient valeur plancher.		I = 1, J = 1 N1,1 = 17

Voir Explications et programmation

CONSTRUCTION avec le cavalier

Les deux règles toutes simples

Règle 1

Mouvement du cavalier : 1 pas vers le haut et 2 pas vers la droite.

Sauf un écart tous les 5 pas (pour un carré magique d'ordre 5)

On notera que l'écart est nécessaire car la case suivante est déjà occupée !

Règle 2

On enroule le tableau comme si les côtés du carré étaient collés :

le haut sur le bas,

et

la gauche sur la droite.

Bilan

Nous avons "enroulé" les nombres à l'intérieur du carré.

Illustration

								8	Etc.
					5		7
				4		6
			3
		2
1

								8	Etc.
					5		7
				4		6
			3
		2
1								8
					5		7
				4		6
			3
		2

1			8						8
	7		5			5		7
44	4			6	4		6
				3
		2

1			8
	7		5
44	4			6
				3
		2

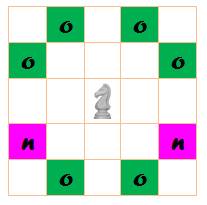
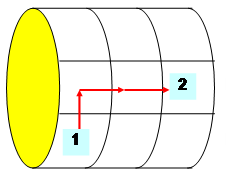
Mouvements du cavalier

Sur les 8 mouvements possibles, seuls 6 donnent lieu à des carrés magiques.

Principe de l'enroulement

Nous avons commencé le carré avec le 1 placé en haut à gauche.

Avec le mouvement du cavalier, le 2 va se retrouver à l'extérieur du carré magique.

La façon de s'en sortir consiste à imaginer que le carré est enroulé sur un tube et que le bas rejoint le haut. Alors le 2 trouve sa place automatiquement.

En déroulant un carré magique en horizontal et en vertical, on forme un tapis sur lequel le carré magique initial est répété.

Le résultat est nommé tapis magique.

Exemple de tapis magique formé avec le carré 3 x 3.

6	1	8	6	1	8	6	1	8
7	5	3	7	5	3	7	5	3
2	9	4	2	9	4	2	9	4
6	1	8	6	1	8	6	1	8
7	5	3	7	5	3	7	5	3
2	9	4	2	9	4	2	9	4
6	1	8	6	1	8	6	1	8
7	5	3	7	5	3	7	5	3
2	9	4	2	9	4	2	9	4

Voir la propriété du tapis magique des carrés magique pandiagonaux

Voir Procédé similaire pour résoudre les énigmes de transvasement

Suite de la construction

En bleu, les nombre que nous avons déjà placés.

En rouge les nouveaux, en appliquant nos deux règles.

On poursuit et on termine

On obtient le carré

magique

panmagique et

associatif soit

diabolique

donné en exemple en première page.

1	15		8
	7		5	14
	4	13		6
12		10		3
9		2	11

1	15	24	8	17
23	7	16	5	14
20	4	13	22	6
12	21	10	19	3
9	18	2	11	25

Carré magique diabolique

Généralisation

Méthode

Cette méthode marche quelle que soit la position du 1 au départ. Et, aussi, quelle que soit la plupart des règles de mouvement que vous prenez pour décrire le carré.

En conséquence, vous pouvez construire quantité de carrés magiques. Un passage sur tableur vous permettra de vérifier si le carré construit est bien magique.

Un peu de théorie

La méthode du cavalier est un cas particulier de la construction siamoise généralisée.

La progression régulière est spécifiée par un vecteur et l'écart est déterminé par un deuxième vecteur.

Les vecteurs sur le premier exemple sont (1, 1) et (0, -1).

Sur le celui du dessous, on a (2, 1) et (1, -1).

17	24	1	8	15
23	5	7	14	16
4	6	13	20	22
10	12	19	21	3
11	18	25	2	9

Carré magique associatif

8	17	1	15	24
5	14	23	7	16
22	6	20	4	13
19	3	12	21	10
11	25	9	18	2

Carré magique panmagique

CONSTRUCTION géométrique

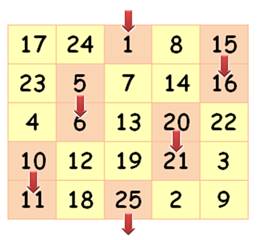
Le principe consiste à placer les nombres dans un losange et de le replier en carré.

On pose les nombres successifs dans le losange, en diagonale, comme indiqué.

On enroule les cases qui dépassent dans le carré magique.

On peut aussi imaginer que l'on pousse les nombres jusqu'au fond du tableau

				1
			6		2
		11		7		3
	16		12		8		4
21		17		13		9		5
	22		18		14		10
		23		19		15
			24		20
				25

				1
			6		2
		11	24	7	20	3
	16	4	12	25	8	16	4
21		17	5	13	21	9		5
	22	10	18	1	14	22	10
		23	6	19	2	15
			24		20
				25

Carré 3x5 – méthode du tapis

Voir Construction avec programme

Voir Magie du carré magique pour autres exemples / Construction du carré magique 13x13

CONSTRUCTION additive

Le principe consiste à sommer les cases de deux carrés latins.

Le premier avec les chiffres de 1 à 5

Pour le construire, on pose cinq fois le 1 en exécutant le mouvement du cavalier.

Même chose pour les autres chiffres.

Le second carré est construit de la même manière en prenant la précaution de ne pas faire le mouvement du cavalier dans la même direction.

On remarquera qu'avec les nombres de 5 en 5 de 0 à 20, ajoutés aux nombres de 1 à 5 du premier tableau, il est possible de former toutes les sommes de 1 à 25.

Pour construire le carré magique, on somme les nombres des cellules deux à deux de chaque tableau.

1	2	3	4	5
4	5	1	2	3
2	3	4	5	1
5	1	2	3	4
3	4	5	1	2

0	15	5	20	10
5	20	10	0	15
10	0	15	5	20
15	5	20	10	0
20	10	0	15	5

1	17	8	24	15
9	25	11	2	18
12	3	19	10	21
20	6	22	13	4
23	14	5	16	7

Voir Suite

Bilan sur les règes de construction Carrés magique associatif d'ordre impair

Le 1 est placé n'importe où, sauf au centre. Lequel est occupé par le nombre (n² + 1) / 2. Le mouvement principal (installation des nombres successifs) s'effectue soit selon la diagonale montante droite ou gauche, soit selon le mouvement du cavalier, soit tout autre espacement. La rupture aux multiples de l'ordre du carré magique devra également s'appliquer pour passer du dernier nombre (n²) au premier (1). Pour un carré associatif, ces deux nombres seront symétriques par rapport à la case centrale (Voir illustration). La méthode est nécessaire mais pas suffisante pour l'obtention d'un carré magique associatif. On vérifiera au tableur le résultat obtenu. Par exemple en plaçant le 1 dans un des coins et en progressant en diagonale, le carré sera imparfait. Exemples avec 1 en coin Mouvement diagonal & Mouvement du cavalier

Voir Exemples d'ordre 9

ENGLISH CORNER
Algorithms. Solutions for the nth order magic square. You can construct any magic square. Put the first number in the middle column of the top row.

Suite	Méthode de Pheru pour le carré 5x5 Toutes les méthodes de construction Carrés diaboliques Carré d'ordre 6 Carrés magiques – Index
Voir	Carrés – les nombres Carrés en géométrie Carrés mystérieux Dominos magiques Énigmes Jeux Nombres en chiffres Nombres magiques - Index Pannumérique Propriétés du carré magique Rubriques débutants Sudoku
Diconombre	Nombre 5 Nombre 25 Nombre 65
Sites	Liens vers les sites carrés magiques
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/CarreMag/CMordr53.htm