|
||||||||||||||||||||||||||||||||
![]()
|
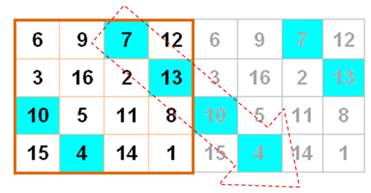
Carrés magiques 4 x 4 Pandiagonaux ou Panmagiques Toutes les diagonales – principales
et partielles – forment des sommes magiques. |
Anglais: Panmagic
square, Pandiagonal square, Nasik square
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Autre manière de voir: l'enroulement du carré sur lui-même, forme
un cylindre vertical.
L'enroulement en reliant le haut et le bas forme un cylindre horizontal. L'enroulement complet forme une sphère. Anglais: The broken
diagonals are the diagonals that wrap round at the edges of the square.
6 + 16 + 11 + 1 = 9 + 2 + 8 + 15 = 7 + 13 +
10 + 4 = 12 + 3 + 5 + 14 = 34 7 + 16 + 10 + 1 = 9 + 3 + 8 + 14 = 6 + 13 +
11 + 4 = 12 + 2 + 5 + 15 = 34
Par exemple, le carré bleu est
magique:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
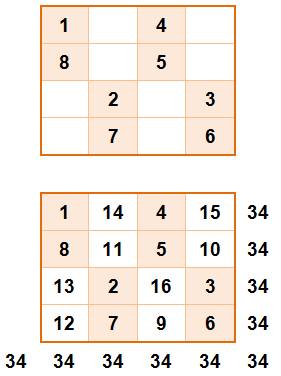
Autres sommes (avec un carré pandiagonal) |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Égalités
remarquables S =
Somme algébrique N =
Quantité de combinaisons
S = 17 0 0 17 N =
8 12 12 8
Forme chapeau Exemple
avec la forme chapeau
Toutes
les formes du chapeau donnent une
égalité: 2 +
7 = 3 + 6 16
+ 9 =
10 + 15 5 +
4 = 8 + 1 11 + 14
= 13 + 12 3 + 10 =
2 + 11 Etc. On
retrouve facilement toutes les sommes et égalités possibles à partir des formules génériques du carré magique pandiagonal. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
24
fondamentaux, 48 par permutations Ces carrés sont
également plus que parfaits
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||
|
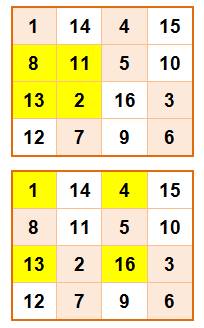
On forme
ce carré en deux temps:
Ce carré
magique est panmagique : magique sur
toutes les diagonales principales et
secondaires, soit 2 x 16 = 32 fois la somme magique 34. Il n'est
pas associatif (somme de deux nombres opposés par
le centre). Un carré
magique plus que parfait est tel que les carrés 2x2 présentent la même somme,
la somme magique: 34. De même pour
tous les carrés3x3, les quatre sommets donnent la somme magique. |
Formation
du carré magique
Somme magique sur carré 2x2 et sommets du 3x3
|
|
Voir
Carré plus que parfait d'ordre 4 –
Développements
![]()
|
Suite |
|
|
Voir |
|
|
Diconombre |
|
|
Sites |
![]()
Renvois
de liens
DIABOLIQUES – Exemple: Carré de Dürer >>>