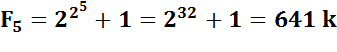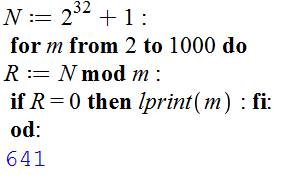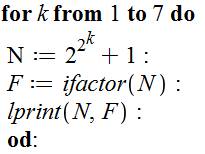|
|||||||||||||||||||||||||||||
![]()
|
DIVISIBILITÉ
p Nombre de Fermat n°5: divisible par 641. Enjeu historique: on
savait que les nombres de Fermat inférieurs à F5 étaient tous premiers. Fermat,
lui-même, conjecturait
qu'ils étaient tous premiers. On sait qu'ils
sont tous composés à partir de F5
et jusqu'à F31. Aujourd'hui: Sachant
que ce nombre est divisible par 641, plusieurs méthodes de calcul sont possibles:
à la main, calculette ou via les congruences
classiquement ou via une astuce. Ne connaissant pas 641, la méthode directe
consisterait à écrire un programme pour détecter cette valeur. |
Voir Règles générales
de divisibilité
|
|
||
|
Le nombre de Fermat F5
est composé. Il est divisible par 641. |
|
|
|
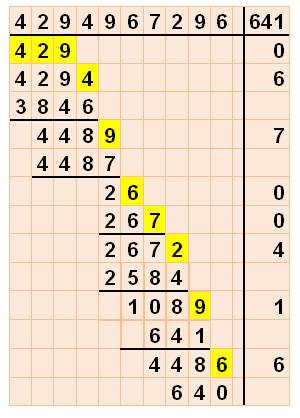
Autres puissances de 2 mod 641 N = r mod m veut dire que N divisé par m donne un reste r. |
232 264 296 etc. |
|
|
|
||
|
Calculette: la touche Mod
permet un calcul immédiat. Sans cette touche, le calcul proposé ci-contre est
facile à réaliser sur la calculette. Les deux touches à utiliser
|
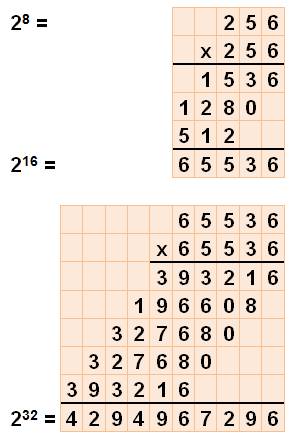
232 = 4 294 967 296; divisé par 32 = 6 700 416,99 et 6 700 416 x
641 = 4 295 159 597 soit 1 de moins que 232. Donc: 232 Certains affirment même que le calcul de la division à la main est un
excellent exercice. Cependant, les démonstrations algébriques ci-dessous
montrent où se nichent les beautés mathématiques. |
|
|
|
||
|
Quel est le reste de la
division de 232 par 641? Notez la tactique algébrique pour s'approcher de 641 et ainsi faire
tous les calculs de tête. On se souviendra que: 640 |
En mod 641: 28
216
= 2828
=
640 x 102 + 256
232
= 216216
= (64 x 3 + 4) (64 x 2 – 7)
= 6 x 64² + 8 x 64 – 21 x 64 – 28
= 64 (384 + 8 – 21) – 28
= 64 x 371 – 28 = 64 (370 + 1) – 28
= 640 x 37 + 64 – 28 = 640 x 37 + 36
232 232 + 1 |
|
|
|
||
|
La barre verticale veut dire: divise. On utilise l'identité remarquable: n4 – 1 = (n + 1) ( …) avec n = 5 x 27 |
641= 54 + 24 = 5 x
27 + 1 641 = (5 x 27)4
+ 232 = (5 x 27)4 – 1 + 1 + 232 641 |
|
|
|
||
|
|
Le programme Maple est archi-simple et son exécution
est instantanée. N prend la valeur du nombre de Fermat. Boucle
avec m qui prend toutes les valeurs de 2 à 1000 (c'est large). R est le reste de la division, cad. le modulo de N par m. Si ce reste est nul, on imprime la valeur de m. Seul résultat: m = 641. |
|
|
|
Même programme pour le nombre de Fermat suivant. Dans ce cas la boucle examine un million de cas
en quelques secondes. |
|
|
5, ``(5) 17, ``(17) 257, ``(257) 65537, ``(65537) 4294967297, ``(641) *``(6700417) etc. |
Ceci-dit, Maple dispose
d'une instruction qui donne la directement factorisation (ifactor). Compte tenu de la quantité de chiffres (78 pour pour F8), la factorisation au-delà de F7
prend énormément de temps et devient vite impossible. |
|
Voir Programmation
– Index
![]()
|
Suite |
|
|
Voir |
|
|
Diconombre |
|
|
Cette page |
![]()