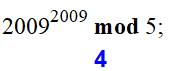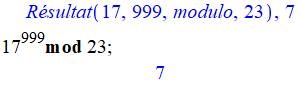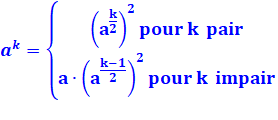|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
CONGRUENCES Exemple de calculs Algorithme de calcul modulaire |
|
|
|||
|
Utilisation
des congruences (modulo) pour
résoudre un problème de pièces de monnaie J'achète 351 euros
avec un lot de pièces de 17 et 18 euros. Combien de pièces de
chaque? |
|||
|
On pose l'équation |
18 x + 17
y |
= 351 |
|
|
On cherche une solution simple, en utilisant le fait que 17 et 18
sont deux nombres
consécutifs |
18
– 17 18 x 351 –
17 x 351 |
= 1 = 351 |
|
|
Retranchons membre à membre
les deux équations |
18 x + 17
y 18 x 351 –
17 x 351 |
= 351 = 351 |
|
|
Résultat |
18(x -
351) |
= – 17(y + 351) |
|
|
Et pour x |
x |
= – 17(y + 351)/18 + 351 |
|
|
Si on divise x par 17, on obtient les restes suivants (x mod 17) |
x mod 17 |
= 0 + 351 mod 17 |
|
|
Or, le reste de 351 par 17 est 11 |
x mod 17 |
= 11 |
|
|
Autrement dit x est un multiple de 17 plus 11 |
x |
= 17 k + 11 |
|
|
Même chose pour y |
y |
= – 18(x - 351) /17
– 351 |
|
|
En reste par 18 |
y mod 18 |
= 9 (ou -9) |
|
|
Valeur de y |
y |
= – 18 k' + 9 |
|
|
Essayons k= k' = 0 |
18 x 11 +
17 x 9 |
= 198 + 153 = 351 |
|
|
Avec d'autres valeurs, on trouve des valeurs trop grandes pour x ou
négatives pour y |
18 x 28 +
17 x 9 18 x 11 –
17 x 9 |
= 657 = 45 |
|
|
Seule solution |
x = 11 |
et y = 9 |
|
|
|
||
|
Démontrez que N = 101 million +
10 est divisible par 13 |
||
|
Avec 10, il manque 3 pour arriver à 13. |
|
|
|
Élévation au carré. Effectivement
100 = 7x13 + 9 |
|
|
|
Poursuivons en prenant le cube. |
|
|
|
Super! Car le 1, élevé à une puissance quelconque, donne toujours 1. |
|
|
|
Pour approcher le million proposé en exposant. |
|
|
|
L'exposant est impair, le signe moins est conservé. |
|
|
|
En multipliant par 10. |
|
|
|
Reste à ajouter 10 pour avoir N. |
|
|
Exemple
donné par Malcom Lines dans:
Dîtes un chiffre – Champs
Flammarion - 1990
|
|
||
|
Calculer le reste de la division par 5 de 20092009 |
|
|
|
On
note que |
|
|
|
Or,
2009 = 3 x 669 + 2 |
|
|
|
Calculer le reste de la division par 5 de 20092009 |
|
|
|
On
note que 2009 = 2010 – 1 |
|
|
|
Rapidement,
on obtient: |
|
|
|
Vérification par logiciel de calcul |
|
|
![]()
|
|
||
|
Particulièrement utile pour calculer les
congruences avec grand exposants (test de
Fermat) Son Principe 1) Calculer les congruences au fur et à mesure
|
Calculez
Base de la méthode
On pourrait calculer au fur et à mesure
Etc. |
|
|
2) En profitant d'une décomposition en puissance de 2 pour accélérer le
calcul |
Accélération avec les puissances de 2 100 = 64 + 32 + 4 = 26 + 25
+ 22 (1100100 en
binaire)
|
|
|
Algorithme Calcul de: ab mod n |
(x, y, z ) = (a, b, 1) – Initialisation Boucle jusqu'à y = 0 Si y est
pair (x, y, z) = ( x² mod n, y/2, z mod n) Si y est
impair (x, y, z) = ( x² mod n,
(y-1)/2, x.z mod n) Résultat = z. |
|
|
|
Commentaires Initialisation d'un triplet (x, y, z) avec a et b
et z = 1 pour commencer. Z sera le résultat du calcul. Lancement de la boucle ave while (tant que). Le nouveau triplet (x, y, z) est calculé selon
les valeurs indiquées dans l'algorithme. Notez que dans le cas impair, la valeur de x est
nécessaire pour calculer z. On prend soin de calculer z avant le nouveau x. Pour illustrer le calcul on imprime les résultats
intermédiaires. Résultats
Notez que dans les résultats intermédiaires, la
première colonne donne x avec ses valeurs pour 17 mod (successivement 1, 2,
4, 8, 16, 32, 64 et 128). La deuxième colonne montre 100 divisé par 2
(valeur entière). La troisième montre le calcul progressif du
modulo. Autre exemple (programme et calcul
direct)
|
Voir Programmation
– Index
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Calcul d'une puissance mod m. Le calcul est accéléré en profitant de cette relation |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Exemple: 31304
(mod 121) Étape 1 – Ligne 1: remplir
les cellules de gauche à droite en
commençant par l'exposant (1304). Si le nombre est pair, le suivant est sa
moitié; sinon soustraire 1.
Étape 2 – Lignes 2, 3 et 4:
on inscrit dans chaque cellule la valeur de 3nombre du haut mod
121. Le
calcul est simplifié en remplissant les cellules de droite
à gauche (donc dans l'autre sens). On profite des résultats
précédents. Exemple: 310 = 35x2
= (35)² soit (1)² en mod 121. Vérification avec logiciel de calcul
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||
|
Calculer le reste de la division par 13 de 20212021 |
|
|||||
|
Premier
pas |
Reduire
la base 2021 |
2021
= 155 x 13 + 6
|
||||
|
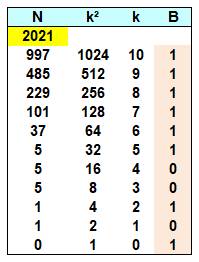
Conversion
en binaire de 2021. On
se souvient que |
|
En
colonnes centrales toutes les puissances de 2 inférieures à 2021. En
colonne de gauche, le nombre N puis sa valeur diminuée des valeurs
successives de 2k. Si le résultat reste positif, un 1 est placé en
colonne de droite (binaire).
Sinon, on conserve la valeur et on place un 0 à droite. La
colonne de droite (B) indique la conversion en binaire de 2021. |
||||
|
Avec
les puissances de 2 |
|
|||||
|
Attention Voir Puissances
à étages |
|
|||||
|
Calcul
des puissances de 6 mod 13 |
… ð [6, 10, 9, 3, 9, 3, 9, 3, 9, 3, 9] |
Multiple
de 13 13,
26, 39, 52, 65, 78, 91, 104, 117, 130, … |
||||
|
Retour
au calcul demandé |
|
|||||
|
Année 2021 en modulo |
2021 = [0, 1, 2, 1, 1, 5, 5, 5, 5, 1,
8, 5, 6, 5, 11, 5, 15, 5, 7, 1] mod (1, 2, 3,.., 13,
…, 20) 20212021 = [0, 1, 2, 1, 1,
5, 3, 5, 2, 1, 8, 5, 2, 3, 11, 5, 2, 11, 11,
1] mod (1, 2, 3,.., 13, …, 20) |
|||||
Voir Nombre
2021
![]()
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
Cette page |
![]()