NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 16/05/2018 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	Diviseurs
Débutants Nombres parfaits	Types de nombres selon leurs diviseurs			Glossaire Diviseurs
INDEX Décomposition Diviseurs	Présentation	Parfait	Presque parfait	Amiables
	de 1 à 100	Démonstration	Unit. Parfait	Sublimes
		Sommaire de cette page >>> Définition >>> Exemple 60 >>> Exemple 90 >>> Liste

Nombres UNITAIREMENT PARFAITS

On considère quelques diviseurs spécifiques d'un nombre. On compare leur somme au nombre initial.

Anglais: Unitary perfect number

Définition
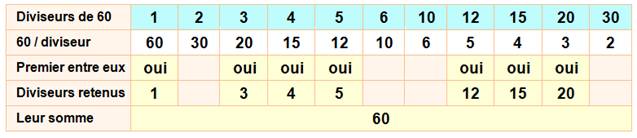
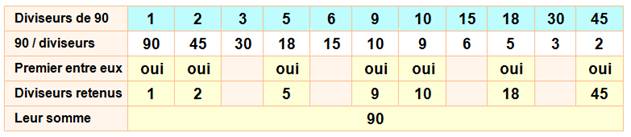
Si d est un diviseur de n et s'il est premier avec n/d, c'est un diviseur unitaire de n. Un nombre unitairement parfait est égal à la somme de ses diviseurs unitaires. Exemple avec 60 La somme des diviseurs unitaires est égal au nombre initial. Le nombre 60 est unitairement parfait. Exemple avec 90

Liste des nombres unitairement parfaits

On n'en connaît que 5.

On conjecture qu'ils sont en nombre limité.

6

60

90

87 360

1,4582... 10^23

Le dernier connu fut découvert par C.R. Wal en 1966l:

146 361 946 186 458 562 560 000 = 2¹⁸ · 3 · 5⁴ · 7 · 11 · 13 · 19 · 37 · 79 · 109 · 157 · 313

Suite	Nombres presque-parfaits Nombres amiables Voir haut de page
Voir	Calcul mental – Index Nombres bons Nombres économes, équidistants et prodigues Théorie des nombres – Index Types de nombres selon leurs diviseurs
Sites	Nombre unitairement parfait – Wikipédia Unitary perfect number – Wolfam MathWorld Super unitary perfect number – Wolfam MathWorld OEIS A002827 – Unitary perfect number
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Decompos/ParfUnit.htm