|
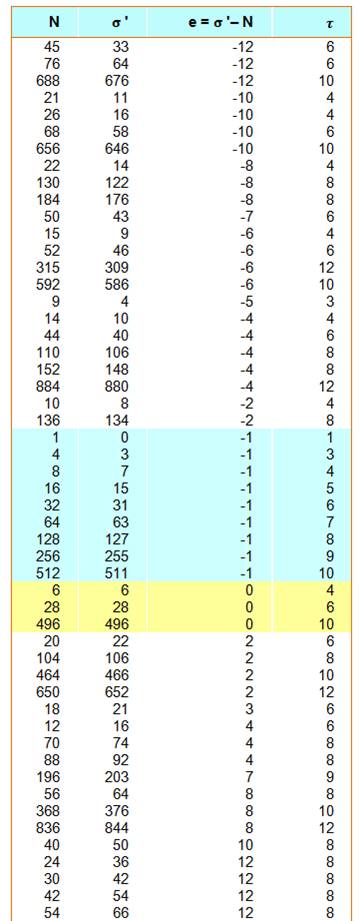
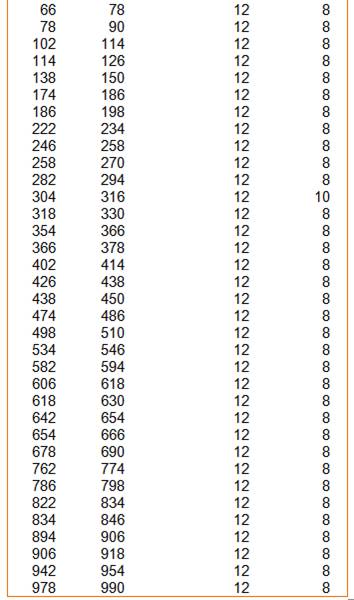
 Surprise de voir apparaître cette longue liste avec 12.
Surprise de voir apparaître cette longue liste avec 12.
 Qu'est-ce qui motive cette différence entre le nombre
et la somme de ses diviseurs propres? Les nombres parfaits! Voyons cela.
Qu'est-ce qui motive cette différence entre le nombre
et la somme de ses diviseurs propres? Les nombres parfaits! Voyons cela.
Observations
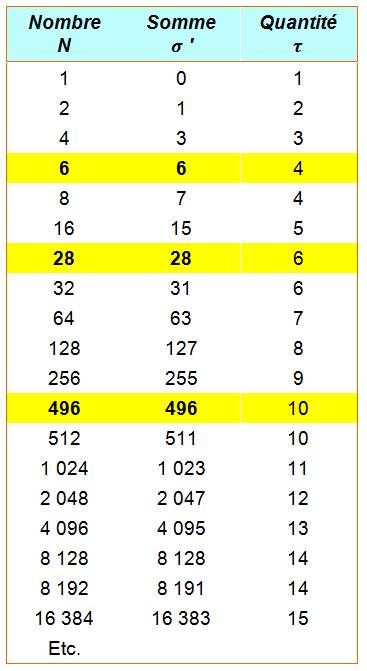
 En observant que quasiment tous ont pour diviseurs (D):
1, 2, 3, et 6, nous introduisons une colonne montrant le quotient N/6.
En observant que quasiment tous ont pour diviseurs (D):
1, 2, 3, et 6, nous introduisons une colonne montrant le quotient N/6.
 À deux exceptions près, ce quotient est la suite des
nombres premiers. et la quantité de diviseurs est égale à 8.
À deux exceptions près, ce quotient est la suite des
nombres premiers. et la quantité de diviseurs est égale à 8.
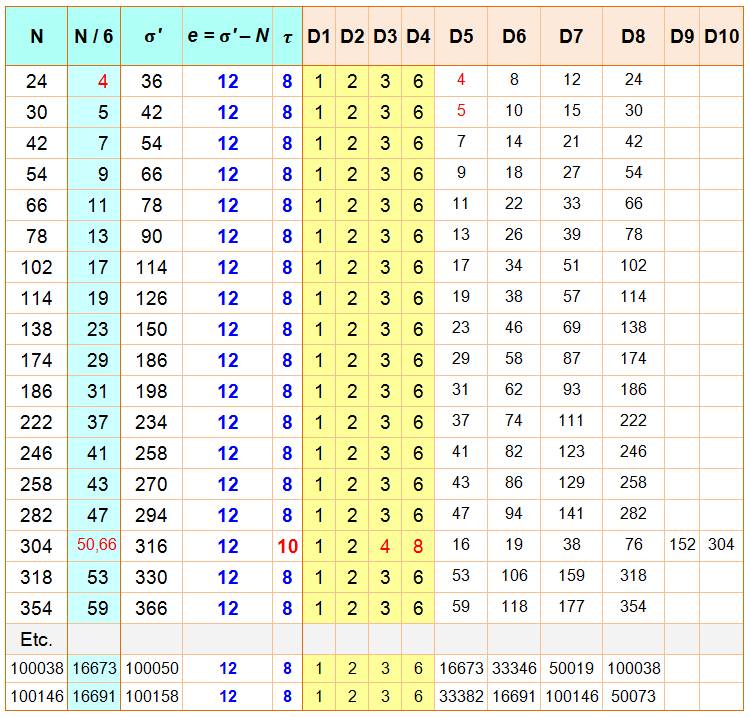
 Il semble donc que, avec P un nombre premier:
Il semble donc que, avec P un nombre premier:
Avec
N = 6P 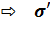 – N = 12 – N = 12
Si N et P
sont premiers entre eux
Démonstration
 Avec N = 6P, ses
diviseurs sont: 1, 2, 3, 6, P, 2P, 3P, 6P.
Avec N = 6P, ses
diviseurs sont: 1, 2, 3, 6, P, 2P, 3P, 6P.
 Quantité:
Quantité: 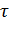 = 8 = 8
 Somme des diviseurs propres:
Somme des diviseurs propres: 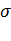 = 1 + 2 + 3 + 6 + P + 2P + 3P = 12 + 6P = 1 + 2 + 3 + 6 + P + 2P + 3P = 12 + 6P
 Différence avec N:
Différence avec N: 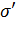 – N = 12 + 6P - 6P = 12 – N = 12 + 6P - 6P = 12
Généralisation
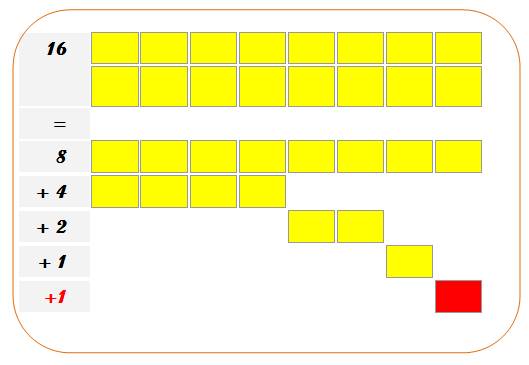
 Cette propriété découle du fait que N = 6 = 1 + 2 + 3 =
Cette propriété découle du fait que N = 6 = 1 + 2 + 3 =
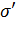 :
nombre parfait :
nombre parfait
 Nous aurions cette propriété avec tout nombre parfait
Nous aurions cette propriété avec tout nombre parfait
 Exclure les nombre N contenant comme diviseur le nombre
premier P. En effet, avec 28, le nombre 196 = 7 x 28 a 9 diviseurs: 1, 2, 4,
7, 14, 28, 49, 98, 196 et non 12 comme attendu pour les autres. La séquence
normale serait : 1, 2, 4, 7, 14, 28, 7, 14, 28,
49, 98, 196 avec trois nombres redondants.
Exclure les nombre N contenant comme diviseur le nombre
premier P. En effet, avec 28, le nombre 196 = 7 x 28 a 9 diviseurs: 1, 2, 4,
7, 14, 28, 49, 98, 196 et non 12 comme attendu pour les autres. La séquence
normale serait : 1, 2, 4, 7, 14, 28, 7, 14, 28,
49, 98, 196 avec trois nombres redondants.
Avec
N = p . P 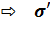 – N = 2p – N = 2p
p, un
nombre parfait; N et P premiers entre eux
|
![]()
![]()
![]()