NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 14/02/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Diviseurs
Débutants Nombres parfaits	Types de nombres selon leurs diviseurs			Glossaire Diviseurs
INDEX Décomposition Diviseurs Types de nombres	Présentation	Parfait	Presque parfait	Amiables
	de 1 à 100	Démonstration	Unit. Parfait	Fiancés
	Admirable	Zumkeller	Amis / Solitaires	Sublimes
		Sommaire de cette page >>> Nombre amiables et sociables >>> Liste des nombres amiables à 5 chiffres >>> Propriétés >>> Critère de Thabit >>> Construction >>> Triplet amiables >>> Nombres sociables ou chaînes amiables >>> Historique >>> Connus et records >>> Chaîne aliquote >>> English corner

Nombres AMICAUX ou Amiables

& Nombres SOCIABLES ou Chaîne Amiable

Nombres FIANCÉS ou quasi-amicaux

Sortes de nombres parfaits mutuels.

Ils sont très rares. On en connaît une centaine seulement.

Ne pas confondre avec nombres amis >>>

Anglais: Amicable numbers, sociable numbers, betrothed numbers

NOMBRE AMIABLES ET SOCIABLES

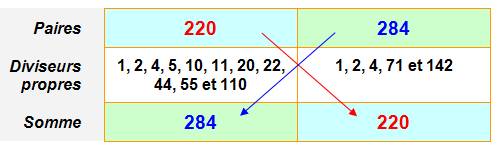
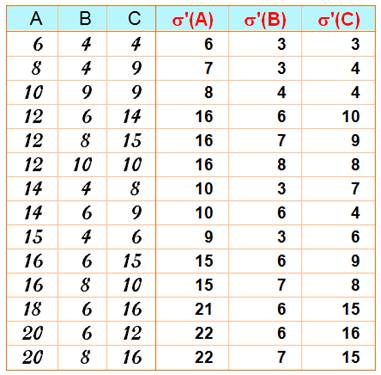
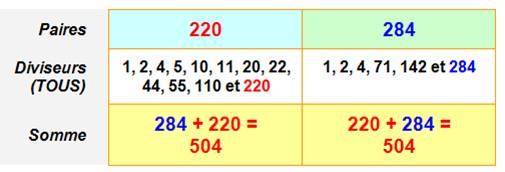
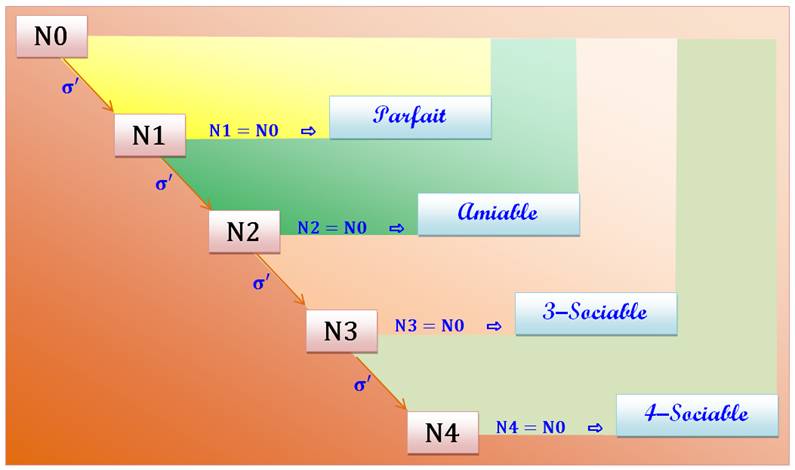
Chaque nombre est la somme des diviseurs propres de l'autre. Les nombres amiables et sociables sont une généralisation de la notion de nombres parfaits. Les nombres amiables sont en couple; les nombres sociables forment une chaine. Exemple: le premier couple amiable Alternative: en prenant tous les diviseurs Définitions Nombres amiables: La somme des diviseurs stricts (hors n) de l'un est égale à l'autre nombre. Ou La somme de tous les diviseurs de l'un est égale à celle de l'autre. Nombres sociables: Boucle de nombres dont le suivant est la somme des diviseurs propres du précédent (le dernier étant bouclé sur le premier). Les nombres amiables forment une boucle avec deux nombres; Les nombres sociables forment une boucle de plusieurs nombres; et Les nombres parfaits forment une boucle sur lui-même. Nombres fiancés ou quasi-amicaux: La somme des diviseurs non-triviaux (hors n et 1) de l'un est égale à l'autre nombre. Nombres amicaux à 1 près.

Voir Brève 11

Illustration

LISTE DES NOMBRES AMIABLES – Jusqu'à 5 CHIFFRES

Rang	N1	N2
1	220	284
2	1 184	1 210
3	2 620	2 924
4	5 020	5 564
5	6 232	6 368
6	10 744	10 856
7	12 285	14 595
8	17 296	18 416
9	63 020	76 084
10	66 928	66 992
11	67 095	71 145
12	69 615	87 633
13	79 750	88 730

Premier couple impair (Descartes):

1 175 265 & 1 438 983

9 437 056 & 9 363 584

Quantité par puissance de 10

Nombre de paires amiables dont le plus petit terme est inférieur à une puissance de 10, celle-ci est repérée par un indice. Il y 13 paires pour n < 10⁵.

1₃, 5₄, 13₅, 42₆, 108₇, 236₈, 586₉, 1427₁₀, 3340₁₁, 7642₁₂, 17519₁₃, 39374₁₄, 87102₁₅, 190775₁₆, 415523₁₇, … OEIS A066873

PROPRIÉTÉS

On ne sait pas s'il y a un nombre infini de paires amicales. On connaît 42 couples inférieurs à 10 000 000. On connaît plus de 1000 paires amiables dont le plus petit nombre est inférieur à un million. La plus grande connue comporte des nombres de 152 chiffres chacun: 3^4 x 5 x 11 x 5 281^19 x 29 x 89 ( 2 x 1 291 x 5 281^19 – 1) 3^4 x 5 x 11 x 5 281^19 x 29 x 89 ( 2^3 x 3^3 x 1 291 x 5 281^19 – 1) Les nombres amiables connus ont la même parité, le plus souvent paire. On ne sait pas s'il existe des paires mixtes, s'ils sont en nombre infini, et il n'existe pas de formules pour les former. On sait former des paires amiables mères ou filles à partir d'une paire primitive. Ce qui pourrait suggérer que les paires amiables sont en nombre infini. Il semble que le quotient de deux nombres amiables tende vers 1. Le plus grand élément d'une paire amiable est déficient. Deux nombres pairs amiables ne peuvent ni l'un ni l'autre être divisibles par 3. Le produit d'une paire mixte (pair x impair) serait supérieur à 10^67 et divisible par 15. Dans chaque couple connu impair - impair, les deux nombres sont des multiples de 3. Il a été conjecturé que c'est une règle générale. Dans presque tous les couples connus pair - pair, la somme des deux nombres est divisible par 9. Il n'y a pas de formule pour calculer toutes les paires amiables.

CRITÈRE DE THABIT

Nombres de Thabit ou Thebit

Les nombres en 3 x 2ⁿ – 1 sont appelés nombres de Thabit (en rouge, premiers):

2, 5, 11, 23, 47, 95, 191, 383, 767,

1 535, 3 071, 6 143, 12 287, 24 575, 49 151, 98 303, 196 607…

Un nombre de Thabit en binaire se présente sous la forme 10 puis n fois le nombre 1.

Par exemple, pour n = 3: T = 23₁₀ = 10111₂.

En effet, on peut écrire: 3 x 2ⁿ – 1 = (2+1) 2ⁿ – 1 = 2ⁿ⁺¹ + (2ⁿ – 1). Soit une puissance de 2 ajoutée à un nombre inférieur de 1 à une puissance de 2.

Par exemple, pour n = 10: 3071 = 2048 + 1023 = 2¹¹ + (2¹⁰ – 1) = 1011 1111 1111.

Voir liste OEIS A055010

Nombres de Riesel

Ils sont définit dans le cadre de la généralisation des nombres de Thabit. On s'intéresse aux nombres de la forme: n = k x 2ⁿ – 1.

Le nombre k, impair, est un nombre de Riesel si tous les nombres n (>0) sont composés. Le plus petit connu est k = 509 203. Il est probable qu'il s'agit du plus petit, sans que ce soit démontré.

Voir développements sur le site Riesel Number – Wolfram MathWorld

Paires amiables

On connaît des formules pour certaines paires particulières, impliquant les nombres de Thabit: 

Si n > 1 et si les nombres suivants sont premiers

p = 3 . 2^{n – 1} – 1

q = 3 . 2ⁿ – 1

r = 9 . 2^{2n – 1} – 1

alors 2ⁿ p . q et 2ⁿ r forment une paire amiable.

Thabit ibn Kurrah (850) - Mathématicien et astronome arabe

Résultats

n = 2	220 & 284	Pythagore
n = 4	17 296 & 18 416	Ibn al-Banna (XIV^e)
n = 7	9 363 584 & 9 437 056	Muhammad Baquir Yazdi (XVII^e)

Seules valeurs connues en 2015.

Exemple pour n= 2

p = 3 x 2^2 – 1 = 11	N = 2^2 . 5 . 11 = 220
q = 3 x 2^1 – 1 = 5	M = 2^2 . 71 = 284
r = 9 x 2^3 – 1 = 71

Il faut reconnaître que ce critère n'est que très peu productif. Il a été établi par un brillant mathématicien musulman: Thabit ibn Qurra. Fermat (1636) redécouvrit ce critère et la paire pour n = 4, de même que Descartes avec la paire pour n = 7. Euler fut le premier mathématicien à explorer et à découvrir de nombreux nombres amiables (plus de 60).

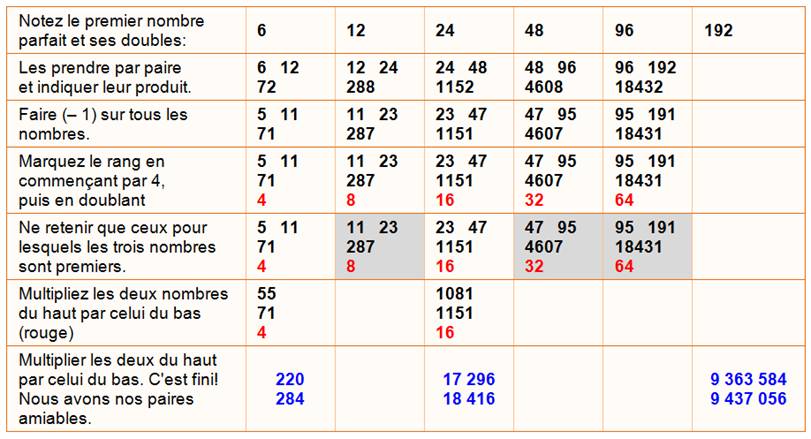
Construction Méthode "recette de cuisine" (basée sur la formule de Thabit)
Méthode laborieuse pour peu de résultats; que ces trois.

D'après Mystères des chiffres de Marc-Alain Ouaknin

TRIPLET AMIABLES
La somme des diviseurs propres de l'un est égale à la somme des diviseurs propres des deux autres. Exemple Ils sont très nombreux, notamment du fait que les nombres premiers produisent un 1. Exemples sans nombres premiers

NOMBRES SOCIABLES OU CHAINES AMIABLES

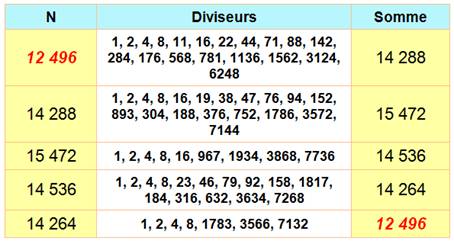
Dans une chaine amiable, chaque nombre est égal à la somme des diviseurs propres du précédent; la somme du dernier étant égale au premier nombre. Les deux premières chaines ont été découvertes en 1918 par Paul Poulet, mathématicien français: 12 496 = 2^4 x 11 x 71 et 14 316 = 2^2 x 3 x 1 193 12 496 Exemple d'une chaine (boucle) de cinq nombres. La somme des diviseurs propres de 12 496 est 14 288, etc. Le nombre 12 496 est dit sociable d'ordre 5. Découvert en 1918 par Poulet. 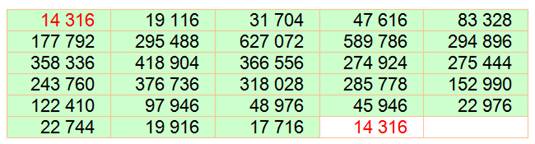Explications 14 316 Exemple d'une chaine (boucle) de 28 nombres. Le nombre 14 316 est sociable d'ordre 28. Découvert en 1918 par Poulet et jamais dépassé jusqu'ne 2012. 1 264 460 Exemple d'une chaine (boucle) de 4 nombres. 1 264 460 = 2^2 x 5 x 17 x 3 719 1 547 860 = 2^2 x 5 x 193 x 401 1 727 636 = 2^2 x 521 x 829 1 305 184 = 2^5 x 40 797

Autres chaines amiables

Jusqu'en 1969, on ne connaissait que ces deux chaînes : 14 316 et 12 496. Henri Cohen a trouvé 7 chaînes à 4 itérations en explorant les nombres jusqu'à 60 millions. D'autres ont été trouvées depuis. On ignore s'il existe des chaînes de longueur quelconque. On n'a jamais trouvé de chaînes de longueur 3. On ne connaît pas de chaîne supérieure à 28. On ne sait pas si la chaine aliquote (chaque nombre suivant est la somme des diviseurs du précédent) se termine toujours par un nombre premier ou par un nombre de la chaine (nombre sociable). La chaine pourrait se perpétuer sans fin?

.

HISTORIQUE

Les nombres amiables ont une longue histoire en magie et astrologie, aphrodisiaques et talismans… Pour se prouvez notre amour: tu manges 220 bonbons et moi 284 ! Il existe des légendes tournant autour de ce thème. Une vielle coutume de numérologiste arabe consistait à inscrire 220 sur un fruit et 284 sur l'autre. Je mange l'un et je donne l'autre à manger à l'être aimé. Ce nombre se trouve dans la Bible: nombre de chèvres offertes par Jacob à Esaü, cadeau amiable? (20 mâles et 200 femelles). Pythagore connaissait ce couple de nombres. Il aurait dit: "Un ami est celui qui est l'autre comme sont 220 & 284" Thabit ibn Qurra(vers 800) découvre une formule pour trouver les paires amicales Au Moyen Âge, ces deux nombres étaient signe d'amour et jouaient un grand rôle dans les horoscopes. Fermat Un nouveau couple de nombres amiables n'a été trouvé qu'en 1636 par Pierre de Fermat: 17 296 & 18 416 dit couple de Fermat. Il avait précédemment été découvert par Al-Farisi (1260-1320). Descartes découvre une nouvelle paire en 1638: 9 363 584 & 9 437 056 dit couple de Descartes. Il avait été découvert par Al-Yazdi vers 1500.   Euler Il donne une liste de 64 paires amiables (avec 2 erreurs). Nicolo Paganini Mais curieusement, le vrai numéro 2 a attendu 1867 pour être déniché par un jeune Italien de 16 ans: 1184 & 1210. Aujourd'hui Toutes les paires jusqu'à 10 chiffres sont connues et quelques autres à plus de chiffres (au total plus de 7500).

HISTORIQUE ET RECORDS

Connus?

Ordre	Type	Historique	Quantité et quelques valeurs
1	Parfait	Antiquité / Euclide	47 Liste >>>
2	Amiable	Bible / Fermat	12 millions Les quinze paires le plus petites: 220 / 284, 1 184 / 1 210, 2 620 / 2 924, 5 020 / 5 564, 6 232 / 6 368, 10 744 / 10 856, 12 285 / 14 595, 17 296 / 18 416, 63 020 / 76 084, 66 928 / 66 992, 67 095 / 71 145, 69 615 / 87 633, 79 750 / 88 730, 79 950 / 138 798, 100 485 / 124 155 … (Ensuite, ils sont > 100 000) Liste vérifiée!
3	Sociable	Aucun trouvé d'ordre 3	0
4	''	Trouvés au XX^e siècle	> 165 Les seize plus petites valeurs: 1 264 460, 2 115 324, 2 784 580, 4 938 136, 7 169 104, 18 048 976, 18 656 380, 28 158 165, 46 722 700, 81 128 632, 174 277 820, 209 524 210, 330 003 580, 498 215 416, 1 236 402 232, 1 799 281 330, …
5	''	La première trouvée - 1918	1 12 496
6	"		5 21 548 919 483, 90 632 826 380, 1 771 417 411 016, 3 524 434 872 392, 4 773 123 705 616
7	"		0
8	"		2 1 095 447 416, 1 276 254 780
9	"		1 805 984 760
28	''	La plus longue trouvée (Poulet – 1918)	1 14 316

Aucun nombre sociable inférieur à 10 000.

Les dix premiers amiables et sociables connus

12496, 14264, 14288, 14316, 14536, 15472, 17716, 19116, 19916, 22744

English corner
Amicable number The number n is amicable if it belongs to an amicable pair. Two numbers n and m are called an amicable pair if the sum of all positive divisors of n is equal to the sum of all positive divisors of m and both are equal to n + m.	Sociable numbers An aliquot sequence is formed by taking an integer, adding all of its divisors other than itself, and then repeating this process with the sum. The numbers for which this process returns to the starting point after more than two steps are called sociable numbers.

Suite	Suite aliquote Nombres amis Nombres sublimes Couples de nombres en puissance Types de nombres par ordre alphabétique Voir haut de page
Voir	Calcul mental – Index Nombres bons Nombres économes, équidistants et prodigues Théorie des nombres – Index Types de nombres selon leurs diviseurs
DicoNombre	Nombre 220 Nombre 1 184 Nombre 2 620 Nombre 12 496 Nombre 14 316
Sites	Known amicable numbers – Liste Perfect, amicable and sociable numbers OEIS A063990 – Amicable numbers
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Decompos/Amiable.htm