|
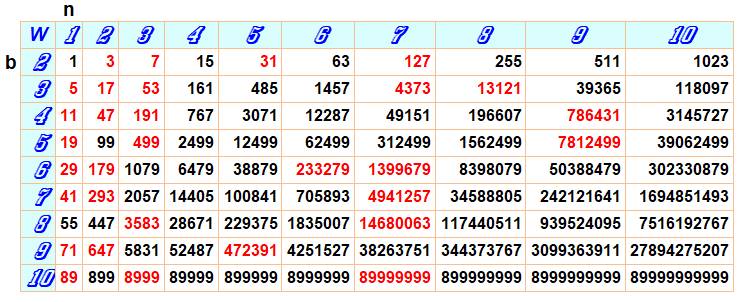
À partir du tableau ci-dessus, pour
chaque base b, on note la valeur de n pour laquelle W est premier.
En base 2, on retrouve les nombres
de Mersenne premiers pour n = 2, 3, 5, 7, 13, 17, …
Avec n = 5: (2 – 1) · 25 – 1 = 31, nombre qui est premier; on
retient n = 5 pour établit la liste ci-dessous.
|
2
|
2, 3, 5, 7, 13, 17,
19, 31, 61, 89, 107, 127, 521, 607, 1279, 2203, 2281, 3217, 4253, 4423,
9689, 9941, 11213, 19937, 21701, 23209, 44497, 86243, 110503, 132049,
216091, 756839, 859433, 1257787, 1398269, 2976221, 3021377, 6972593,
13466917, 20996011, 24036583, 25964951, 30402457, 32582657, 37156667,
42643801, 43112609, 57885161, 74207281, 77232917, 82589933, ...
|
A000043
|
|
3
|
1, 2, 3, 7, 8, 12,
20, 23, 27, 35, 56, 62, 68, 131, 222, 384, 387, 579, 644, 1772, 3751, 5270,
6335, 8544, 9204, 12312, 18806, 21114, 49340, 75551, 90012, 128295, 143552,
147488, 1010743, 1063844, 1360104, ...
|
A003307
|
|
4
|
1, 2, 3, 9, 17, 19,
32, 38, 47, 103, 108, 153, 162, 229, 235, 637, 1638, 2102, 2567, 6338,
7449, 12845, 20814, 40165, 61815, 77965, 117380, 207420, 351019, 496350,
600523, 1156367, 2117707, 5742009, 5865925, 5947859, ...
|
A272057
|
|
5
|
1, 3, 9, 13, 15, 25,
39, 69, 165, 171, 209, 339, 2033, 6583, 15393, 282989, 498483, 504221,
754611, 864751, ...
|
A046865
|
|
6
|
1, 2, 6, 7, 11, 23,
33, 48, 68, 79, 116, 151, 205, 1016, 1332, 1448, 3481, 3566, 3665, 11233,
13363, 29166, 44358, 58530, 191706, ...
|
A079906
|
|
7
|
1, 2, 7, 18, 55, 69,
87, 119, 141, 189, 249, 354, 1586, 2135, 2865, 2930, 4214, 7167, 67485,
74402, 79326, ...
|
A046866
|
|
8
|
3, 7, 15, 59, 6127,
8703, 11619, 23403, 124299, ...
|
A268061
|
|
9
|
1, 2, 5, 25, 85, 92,
97, 649, 2017, 2978, 3577, 4985, 17978, 21365, 66002, 95305, 142199, ...
|
A268356
|
|
10
|
1, 3, 7, 19, 29, 37,
93, 935, 8415, 9631, 11143, 41475, 41917, 48051, 107663, 212903, 223871,
260253, 364521, 383643, 1009567, ...
|
A056725
|
Les nombres premiers [41, 43, 53, 67,
71, 73, 83, 101, 109, …] sont les plus petits à ne pas figurer dans le
tableau.
|
![]()
![]()
![]()