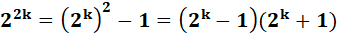NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 14/08/2019 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	PUISSANCE de 2
Débutants Puissance	Nombres de Fermat et Mersenne		Glossaire Puissance
INDEX Puissance Décomposition Puissance de 2	FERMAT (biographie)	MERSENNE (biographie)
	Nombres de Fermat	Nombres de Mersenne
	Valeurs et facteurs	Valeurs et facteurs
	Diviseurs	Mersenne – Records
		Mersenne composés
	Diviseurs	Carol et Kynea
	Sommaire de cette page >>> Mn = 2^n – 1 >>> Si n est composé, alors 2n – 1 est composé – Démo >>> 2^2k – 1 est divisible par 3 >>> 2^3k – 1 est divisible par 7 >>> 2^5k – 1 est divisible par 31 >>> 2^nk – 1 est divisible par 2^n – 1 >>> PRIMALITÉ des nombres de Mersenne

NOMBRES de MERSENNE

M_n = 2ⁿ – 1

Premiers ou composés?

Voir Premier / Composé / Facteurs

En bref

Mn = 2^n – 1
n = p premier Un nombre 2^p – 1 n'est premier (nombre de Mersenne) que si p est premier, mais pas toujours.
Mersenne premiers avec p = 2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107, 127, 521, 607, 1279, 2203, 2281, 3217, 4253, 4423, 9689, 9941, 11213, 19937, 21701, 23209, 44497, 86243, 110503, 132049, 216091, 756839, 859433, 1257787, 1398269, 2976221, 3021377, 6972593, 13466917, 20996011, 24036583, 25964951, 30402457, 32582657, 37156667, 42643801, 43112609, … Voir Liste des records	Mersenne composé avec p = 11, 23, 29, 37, 41, 43, 47, 53, 59, 67, 71, 73, 79, 83, 97, 101, 103, 109, 113, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, … Aucune preuve que cette suite est infinie.
n composé Un nombre 2^n – 1 avec n composé est toujours composé.
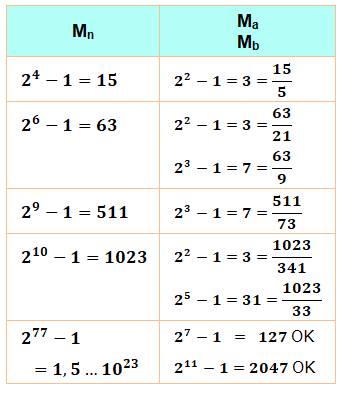
Théorème Si n = a.b alors Ma et Mb divisent Mn. Exemples	Cas des indices pairs La factorisation est immédiate via une identité remarquable 2^4 – 1 = (2^2 – 1)(2^2 + 1) = 3 x 5 = 15 2^6 – 1 = (2^3 – 1)(2^3 + 1) = 7 x 9 = 63 2^8 – 1 = (2^4 – 1)(2^4 + 1) = 15 x 17 = 255 … 2^2n – 1 = (2^n – 1)(2^n + 1) Cas d'un indice multiple d'un premier 2^2k – 1 divisible par 2^2 – 1 = 3 2^3k – 1 divisible par 2^3 – 1 = 7 2^5k – 1 divisible par 2^5 – 1 = 31 2^7k – 1 divisible par 2^7 – 1 = 127 2^11k – 1 divisible par 2^11 – 1 = 2047 … Simple application du théorème cité à gauche.

Si n est composé, alors 2^n – 1 est composé – Démo
Démonstration 1	Classique par factorisation
Prenons	n = a.b avec a et b > 1
On a, avec m = 2^a
Factorisation
Facteurs plus grands que 1
Bilan	Avec deux facteurs plus grands que 1, ce nombre 2^n – 1 est composé.

Démonstration 2	Utilisation des congruences (modulo)
Prenons	q = 2^n – 1
Sous la forme de congruence
Puissance m
Conclusion pour le nombre composé n.m

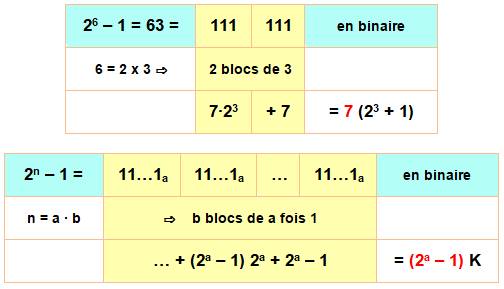
Démonstration 3		Utilisation de la forme binaire des puissances de 2 qui indique le facteur de divisibilité
Forme binaire	2^3 – 1 = 7 = 111En binaire: trois fois le chiffre 1 2^6 – 1 = 63 = 111111En binaire: six fois le chiffre 1 2^n – 1 = 1111…1 En binaire: n fois le chiffre 1
Exemple avec 6 et généralisation avec n Résultat avec a; on a la même chose en prenant b.

Démonstration 4	Utilisation
Prenons et Considérons	n = a.b avec a et b > 1 Mn = 2^n – 1 , Ma = 2^a – 1, Mb = 2^b – 1
Écrivons	Mab = 2^ab – 1 = (2^a)^b – 1
On a	Ma = 2^a – 1 => 2^a = Ma + 1
Ce qui donne	Mab = (Ma + 1)^b – 1
Développement de la puissance. Tous les termes sont en k.Ma sauf le produit des 1.	Mab = Ma (…+…+…) + 1 – 1 = Ma (…+…+…)
Conclusion	Ma divise Mab = Mn

Démonstrations complémentaire pour le plaisir …

2^2k – 1 est divisible par 3
Exemples	2^2 – 1 = 4 – 1 = 3 2^4 – 1 = 16 – 1 = 15 = 2 x 6 + 3 2^6 – 1 = 64 – 1 = 63 = 10 x 6 + 3 Ils sont tous composés, divisibles par 3 et tous avec un reste 3 lorsque divisés par 6.
Factorisation	Nombre composé
Divisible par 3	Parmi les deux nombres de part et d'autre d'un nombre pair, l'un des deux est divisible par 3. Exemple: 15, 16, 17

Démo express	2^2k = 4^k 1 mod 3 2^2k – 1 0 mod 3 => 2^2k – 1 est divisible par 3
Et pour 6 ?	2^2k = 4^k 4 mod 6 2^2k – 1 3 mod 6 => 2^2k – 1 divisé par 6 donne un reste de 3.

2^3k – 1 est divisible par 7 = 2^3 – 1
Exemples	2^3 – 1 = 8 – 1 = 7 2^6 – 1 = 64 – 1 = 63 = 7 x 9 Note: 2^6 – 1 = (2^3 – 1) (2^3 + 1) = 7 x 9
Un calcul particulier	2^9 = 2^6+3 = 2^6 x 2^3 = 2^6 (1 + 2^3 – 1) = 2^6 x 2^6 (2^3 – 1 ) = 64 + 7 x 64
Récurrence
Avec le -1
Héritage	Si on suppose que 2^3k – 1 est divisible par 7, alors son successeur 2^3(k + 1) – 1 est aussi divisible par 7 (jaune).
Induction	La proposition "2^3k – 1 est divisible par 7" est vraie pour k = 1 et, si elle est vraie pour k elle est aussi vraie pour k + 1, alors elle est vraie pour tout k.

2^5k – 1 est divisible par 31 = 2^5 – 1 2^7k – 1 est divisible par 127 = 2^7 – 1 Etc.
Exemples	2^5 – 1 = 32 – 1 = 31 2^10 – 1 = 1024 – 1 = 1023 = 31 x 33 Note: 2^10 – 1 = (2^5 – 1) (2^5 + 1) = 31 x 33
Un calcul particulier	2^15 = 2^10+5 = 2^10 x 2^5 = 2^10 (1 + 2^5 – 1) = 2^10 x 2^10 (2^5 – 1 ) = 1024 x + 31 x 1024
Récurrence
Avec le -1
Héritage	Si on suppose que 2^5k – 1 est divisible par 31, alors son successeur 2^5(k + 1) – 1 est aussi divisible par 31 (jaune).
Induction	La proposition "2^5k – 1 est divisible par 31" est vraie pour k = 1 et, si elle est vraie pour k elle est aussi vraie pour k + 1, alors elle est vraie pour tout k.
Démo express	2^5n – 1 = (2^5)^n – 1 = (2^5 – 1) (2^5(n-1) + 2^5(n-2) + … 2^5 + 1 ) = 31 . k

Voir Divisibilité par 31

Soit, une nouvelle variante des démonstrations initiales

Si n est composé, alors 2^n – 1 est composé
Nous avons vu et on aurait	2^3k – 1 est divisible par 7 = 2^3 – 1 2^5k – 1 est divisible par 31 = 2^5 – 1 2^7k – 1 est divisible par 127 = 2^7 – 1 2^11k – 1 est divisible par 2047 = 2^11 – 1 … 2^pk – 1 est divisible par 2^p – 1
D'une manière générale	^Si n est décomposé en facteurs premiers Alors: 2^n – 1 est divisible par 2^m – 1
Exemples	Avec 20 = 2^2x 5 2^20x1 – 1 est divisible par 2^10 – 1 = 1023 2^20x2 – 1 est divisible par 2^10 – 1 2^20xk – 1 est divisible par 2^10 – 1 Avec 540 = 2^2x 3^3 x 5 2^540x2 – 1 est divisible par 2^540 – 1

PRIMALITÉ des nombres de Mersenne
On prouve la primalité d'un nombre de Mersenne grâce au test de Lucas-Lehmer, basé sur la propriété suivante => C'est avec ce test que Lucas a réussi à factoriser 2^127 – 1. C'est avec ce test que sont connus les plus grands premiers actuellement (1999).	2^p – 1 est premier si et seulement si 2^p – 1 divise SP Sn étant la suite ainsi définie:  avec S2 = 4 et Sn+1 = Sn² – 2 Les premiers termes de la suite sont: 4, 14, 194, 37 634, …

Voir Test de primalité de Lucas-Lehmer

CALCULS
p	Mp = 2^P – 1	S(p–1)	S(p–1) / Mp	Mersenne Premier
3	7	14	2	OUI
4	15	194	194/15	Non
5	31	37634	1214	OUI
6	63	1416317954	1416317954/63	Non
7	127	2005956546822746114 = 0,200596 10^19	15794933439549182	OUI
8	255	4023861667741036022 825635656102100994 = 0,402386 10^37		Non
9	511	0,1619146272 10 ^74		Non
10	1 023	0,2621634650 10^147		Non
11	2 047	0,6872968241 10 ^293		Non
12	4 095	0,4723769244 10 ^586		Non
13	8 191	0,2231399587 10 ^1 172	568 chiffres!	OUI

Suite et Retour	Mersenne – Nombres Mersenne – Table des nombres et records Mersenne – Table des facteurs Fermat Divisibilité par k de certaines expressions Puissances de 2
Voir	Carrés Magiques Géométrie – Index Humour – Index Jeux – Index Nombres composés Nombres magiques Rubriques débutants Théorie des nombres Tous les types de premiers
Sites	Sequence of Composite Mersenne Numbers – Proof Wiki OEIS 000043 – Mersenne exponents: primes p such that 2^p – 1 is prime. Then 2^p – 1 is called a Mersenne prime OEIS 054723 – Prime exponents of composite Mersenne numbers OEIS A135980 – Numbers n such that the Mersenne number 2^Prime[n] – 1 is composite
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Decompos/MersennC.htm