NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 23/05/2022 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Carrés magiques
Débutants Carrés magiques	Généralités				Glossaire Carrés magiques
INDEX Carrés magiques Jeux	Débutant	Introduction	Type	Construction
	Somme	Quantité	Dénombrement	Maths
	Vocabulaire	Symétrie	Sites
		Sommaire de cette page >>> Approche des carrés magiques >>> Carré magique ou diabolique >>> Introduction aux carrés magiques >>> Somme magique >>> Ordre du carré magique >>> Curiosités et propriétés >>> Suite

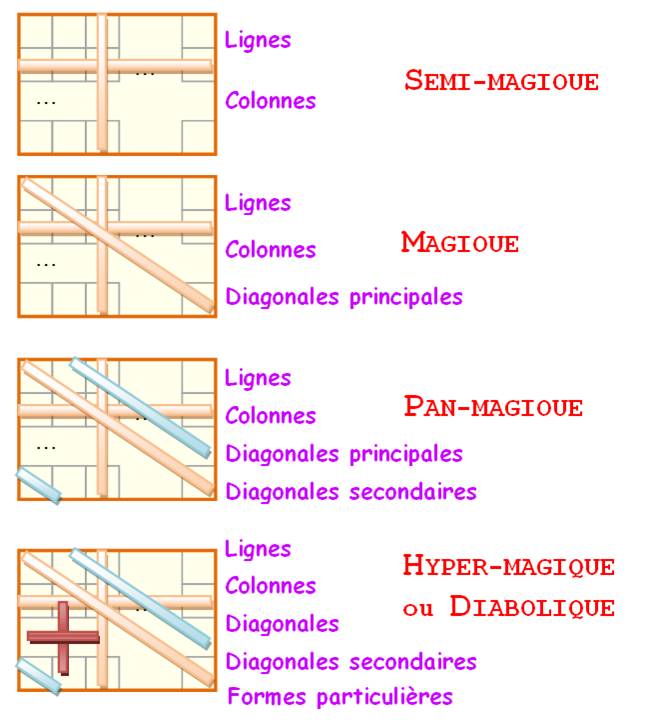
Récréations mathématiques combinatoires CARRÉS MAGIQUES Ces pages me donnent un peu d'émotion… Très jeune (moins de dix ans), j'ai découvert les carrés magiques. Leur pratique m'a donné la passion des nombres, des mathématiques et mon goût pour les curiosités arithmétiques associées. Voir, en particulier, la méthode de construction des carrés magiques avec le mouvement du cavalier. Si vous n'avez jamais entendu parler des carrés magiques, allez à: La magie du carré 3 x 3.

Carré de Lo Shu Chine, il y a 3000 ans Notez la manière de représenter les nombres de 1 à 9

Il n'y aucune science qui enseigne l'harmonie de la nature plus clairement que les mathématiques, et les carrés magiques sont comme un miroir qui reflète la symétrie de la norme divine immanente à toute chose, dans l'immensité incommensurable du cosmos et dans la construction de l'atome et pas moins que dans les profondeurs mystérieuses de l'esprit humain

Paul Carus (1852-1919) - Professeur de philosophie.

Il a développé le bouddhisme en Amérique

Cité par Michael Wade Lillegard – Magic boxes

Voir Pensées & humour

APPROCHE

Voici un carré magique et diabolique de 5 x 5 cases

Amusez-vous à trouver toutes les configurations de 5 cases dont la somme est constante et égale à la somme magique 65.

Sommes classiques du carré magique

	1	15	24	8	17	S = 65
	23	7	16	5	14	S = 65
	20	4	13	22	6	S = 65
	12	21	10	19	3	S = 65
	9	18	2	11	25	S = 65
D = 65	S = 65	S = 65	S = 65	S = 65	S = 65	D = 65

Constante magique = 65

= S = somme sur les lignes ou sur les colonnes.

= D = somme sur l'une ou l'autre des diagonales.

Observation: la somme sur les extrémités en diagonale vaut deux fois 13, le nombre du centre:

26 = 2 x 13 = 1 + 25 =  15 + 11 + … 7 + 19 = 16 + 10 …

Notez également que 13 x 5 = 65; 13 est la valeur moyenne de chaque case du carré magique.

Autres configurations magiques

Somme en croix droite

1	15	24	8	17
23	7	16	5	14
20	4	13	22	6
12	21	10	19	3
9	18	2	11	25

La somme des nombres dans

la croix bleue donne 65.

Déplacez la croix, vous aurez encore 65.

Somme en croix de Saint-André

1	15	24	8	17
23	7	16	5	14
20	4	13	22	6
12	21	10	19	3
9	18	2	11	25

La somme des nombres dans

la croix bleue donne 65.

Déplacez la croix, vous aurez encore 65.

Carrés magiques: les cinq types principaux

Voir suite en Types de carrés magiques

INTRODUCTION AUX CARRÉS MAGIQUES

Carré magique, en mathématiques: tableau de nombres distincts, en général de 1 à n, rangés dans un carré, de sorte que les sommes des nombres sont égales sur, au moins,

chaque ligne,

chaque colonne, et

chaque diagonale principale.

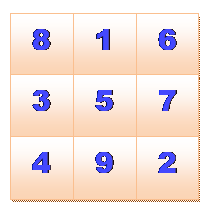
Par exemple, le tableau carré

6	1	8
7	5	3
2	9	4

C'est un carré magique d'ordre 3. L'ordre est le nombre de lignes ou de colonnes.

La somme magique pour un carré magique d'ordre 3 vaut 15.

Observations

Dans les temps anciens, de tels arrangements de nombres étaient considérés comme des porte-bonheur ou des talismans.

Plus tard, les mathématiciens s'intéressèrent aux carrés magiques en tant que problèmes d'analyse mathématique.

En général, on utilise les nombres successifs à partir de 1.

Pour un carré d'ordre 3 (côté = 3), il faudra les chiffres de 1 à 9.
Mais on peut aussi jouer avec d'autres suites de nombres.

SOMME MAGIQUE
Un carré magique d'ordre n utilise les entiers:  1, 2, 3, ... n² La somme de 1, 2, 3,...n² est: n² (n² + 1) / 2 Par conséquent, la somme S de chacune des n lignes, de chacune des n colonnes, ou de chacune des deux diagonales principales du carré magique, est donnée ci-contre selon l'ordre n du carré	Constante magique S S = n (n² + 1) / 2 n = 3 S = 15 4 34 5 65 6 111 7 175 8 260 9 369 10 505
La somme magique est parfois présente pour d'autres configurations de n cases dans le carré. C'est souvent le cas pour les diagonales secondaires, ou couplées ou pandiagonales. Exemple sur le carré 5x5 du haut de page: 15 +16 + 22+ 3 + 9 = 65 Lorsque d'autres configurations géométriques, comme des croix, se présentent avec la constante magique, le carré magique est dit diabolique	Lignes Colonnes Diagonales + éventuellement Pandiagonales Croix Autres formes

ORDRE du carré magique

Ordre du carré magique: quantité de cellules par côté du carré magique de lignes, ou de colonnes. Ordre 1: une infinité de carrés triviaux Le carré n'existe pas (ou alors trivial, car c'est un nombre isolé). Ordre 2: impossible Avec les nombres de 1 à 4 sur un carré 2 x 2, il est impossible de créer une constante magique. Le 2 est symbole du chaos pour Pythagore. Ordre 3: un unique carré magique Il existe bien un carré 3 x 3 et il est unique, aux permutations près Ordre 4: il y en a 880! À partir de l'ordre 4, et au-delà, la quantité de carrés magiques croît rapidement.

Curiosités / Propriétés

Le carré magique formé des éléments 1, 2,..., n ² existe pour tout ordre n, hormis pour n = 2. Cependant, on ne connaît pas à ce jour de règle générale permettant de construire tous les carrés magiques, et on ne sait pas combien il existe de carrés magiques pour chaque ordre n. Des règles de construction ont été développées pour trois catégories de carrés magiques particuliers : ceux pour lesquels l'ordre n est impair, ceux pour lesquels l'ordre n est divisible par 2 mais pas par 4, ceux dont l'ordre n est divisible par 4. Le carré magique est doublement magique s'il reste magique lorsque chaque élément est remplacé par son carré. Il est triplement magique s'il reste magique lorsque chaque élément est remplacé par son carré et par son cube. Les cubes magiques et autres figures géométriques magiques ont également fait l'objet d'études.

À SUIVRE …

Les carrés magiques sont fascinants par leurs diversités, leurs quantités, la manière de les construire. La table des matières vous permet de vous orienter dans ce monde foisonnant des carrés magiques de tout type. Une page pour les débutants, les novices … vous fera y entrer en douceur. Un glossaire vous donnera tout le vocabulaire afférent aux carrés magiques. Vous pourrez aussi fureter sur Internet avec une liste de liens utiles. Bon amusement …

ENGLISH CORNER

Recreational mathematics: a magic square of order n is an arrangement of n² numbers, usually distinct integers, in a square, such that the n numbers in all rows, all columns, and both diagonals sum to the same constant. The magic lies in the fact that the numbers in each row, column, and diagonal always sum to the same number, called the magic constant. If the integers are consecutive numbers from 1 to n², the square is said to be of nth order. An nth-order magic square is a square array of n² distinct integers.

Suite	Carré 3 x 3 Carrés magiques – Index
Voir	Algorithmes Bi, tripartitions Carrés – les nombres Carrés en géométrie Carrés mystérieux Dominos magiques Géométrie Humour Jeux Jeux de chiffres Jeux de chiffres Magie – Index Nombres consécutifs Nombres magiques - Index Pannumérique Panorama Rubriques débutants Sudoku
Diconombre	Nombre 3 Nombre 9 Nombre 15
Sites	Liens vers les sites carrés magiques
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/CarreMag/CMIntro.htm