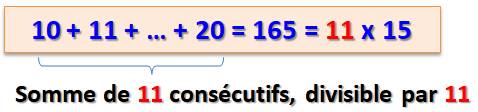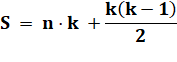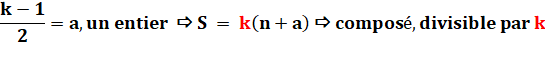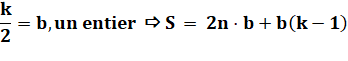NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 14/02/2025 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	DIVISIBILITÉ
Débutants Division	Somme			Glossaire Division
INDEX Divisibilité	Général	Somme de q par q	Consécutifs	Nombres polis
		Sommaire de cette page Tables >>> Partitions en nombres consécutifs >>> Quantités record de partitions Propriétés >>> Partition avec consécutifs – Propriétés >>> Observations sur la divisibilité de la somme >>> Mise en tableau >>> Explications >>>Démonstration >>> Bilan

SOMME de nombres CONSÉCUTIFS

1) Quels sont les nombres dont la partition est une somme de nombres consécutifs?

Exemples de partitions avec nombres consécutifs

Tous les nombres impairs sont somme de deux consécutifs.

Les puissances de 2 ne sont jamais sommes de consécutifs.

Le plus petit nombre avec deux telles partitions est 9 = 4 + 5 = 2 + 3 + 4.

2) Divisibilité de la somme de n nombres consécutifs?

Théorèmes sur la divisibilité d'une somme de consécutifs

La somme de 2k consécutifs est divisible par k.

La somme de 2k+1 consécutifs est divisible par 2k.

Le résultat est simple à trouver. Sa recherche peut faire l'objet d'un bon exercice sur tableur.

Voir Le produit de p nombres consécutifs est divisible par factoriel p >>>

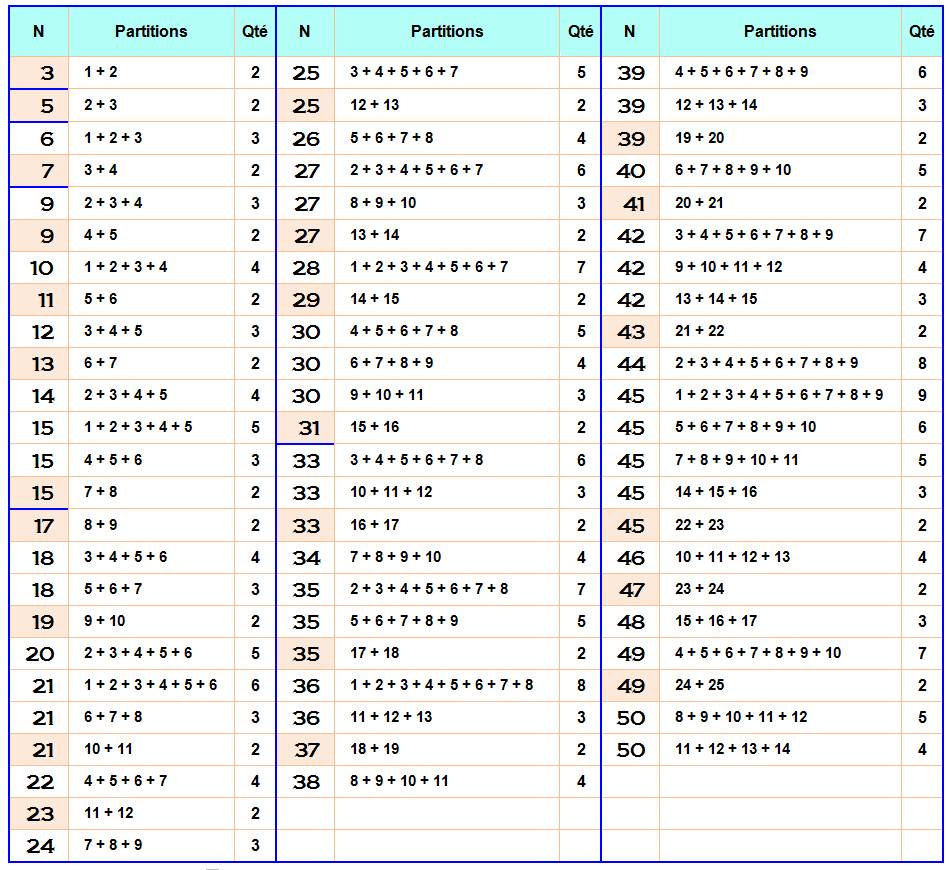
Table des partitions avec nombres consécutifs jusqu'à n = 50

Voir Tables – Index

Quantité de partitions en nombres consécutifs Records pour N jusqu'à 10 000
On s'intéresse aux multiparitions des nombres avec des nombres consécutifs. On note les premiers nombres à présenter une plus grande mutirépratition que le précécent (record). Le nombre 9 a deux telles partitions; le suivant est 15 avec trois telles partitions; etc. Pour ne pas charger l'écriture, un indice indique la quantité de termes dans l'addition: 7 + …+ 115 signifie: 7 + 8 + 9 + 10 + 11 (cinq termes).
Liste Nombres hautement composés impairs qui sont aussi les nombres qui posèdent le record de sommes de nombres consécutifs. OEIS A053624 – Highly composite odd numbers: odd numbers where d(n) increases to a record.		1, 3, 9, 15, 45, 105, 225, 315, 945, 1575, 2835, 3465, 10395, 17325, 31185, 45045, 121275, 135135, 225225, 405405, 675675, 1576575, 2027025, 2297295, 3828825, 6891885, 11486475, 26801775, 34459425, 43648605, 72747675, 130945815, ..

Voir Table – Index

Partitions avec des consécutifs – Propriétés

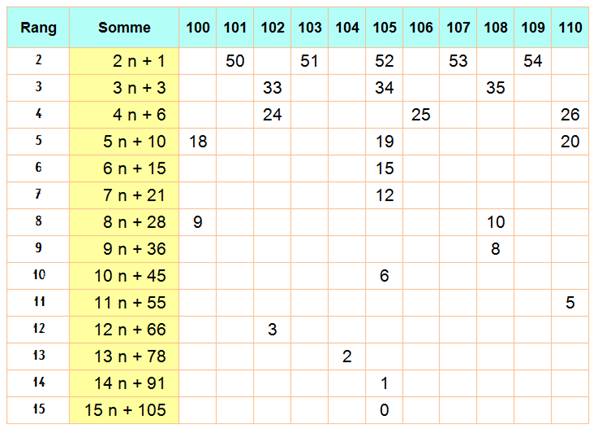
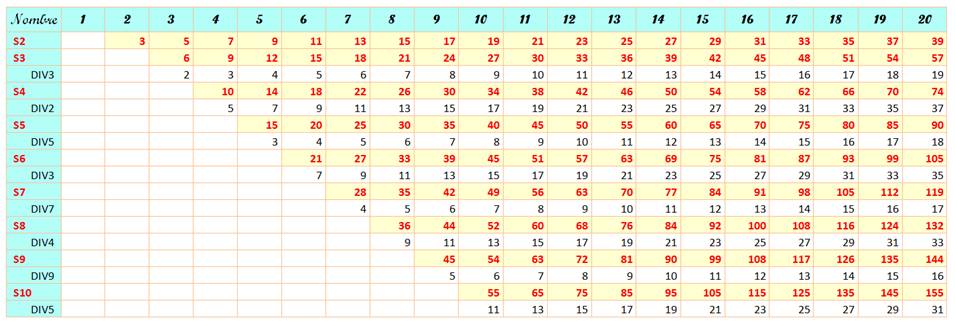
La somme de k nombres consécutifs est égale à: n + (n+1) + (n+2) + … + (n+k) = kn + Tk avec Tk le nombre triangulaire de rang k. Ce tableau récapitule les formules pour k = 2 à 15 et montre les possibilités de partitions pour les nombres de 100 à 110. Par exemple: À la ligne 5 du tableau, avec n = 18, la somme est égale à 5 x 18 + 10 = 100. Ce qui veut dire que la partition de 100 commence par 18 avec 5 termes soit: 100 = 18 + 19 + 20 + 21 + 22 Autres exemples: 10 x 6 + 45 = 105 = 6 + 7 + 8 + 9 + 10 + 11 + 12 + 13 + 14 + 15 = 5 x 21 14 x 1 + 91 = 105 = 1 + 2 + …. + 14 = 14 x 15 / 2 = 105 15 x 0 + 105 = 105 = 0 + 1 + 2 + …. + 14 Sur la colonne du 105, on retrouve le fait que 105 est sept fois partition de consécutifs (huit avec le cas trivial incluant le 0 initial).

Retour Partitions avec nombres consécutifs

Observations sur la divisibilité de la somme de consécutifs
Un petit exercice sur tableur va nous permettre de faire les observations souhaitées. En haut la suite des nombres entiers. En S2 pour somme de deux consécutifs, la somme du nombre au-dessus et son prédécesseur. Comme 11 = 6 + 5. En S3, la somme de trois consécutifs, et en Div3, le quotient de cette somme divisée par 3. Etc.

Les sommes du type S3, S5, S7, S9 … S_Impair sont divisibles par 3, 5, 7, 9…, Impair.

Les sommes du type S4, S6, S8, S10 … S_Pair sont divisibles par Pair / 2.

Mise en tableau
Établissons le tableau indiquant la divisibilité des sommes Sn. En vert, mise en évidence du constat que nous avons fait. Les nombres négatifs de la diagonale indique que ces sommes seraient divisibles si on leur retire ce nombre. Exemple S4 - 2 est divisible par 4. En effet s4 = {10, 14, 18 …}. Les fractions1/2 et 1/3 indiquent que les sommes sont divisibles une fois sur 2 ou sur 3.

Explications
Est-ce magique? Quelle est le mystère? Pour débusquer la règle, mettons les nombres consécutifs sous la forme n, n + 1, n + 2 … et effectuons la somme. Par exemple: sur la colonne S3, on trouve: n + 2 qui est bien le troisième nombre consécutifs; 3n + 3 qui est la somme de n + (n+1) + (n+2); et Cette somme est divisible par 3.

Voir Somme de 12 entiers consécutifs, jamais carré

Démonstration
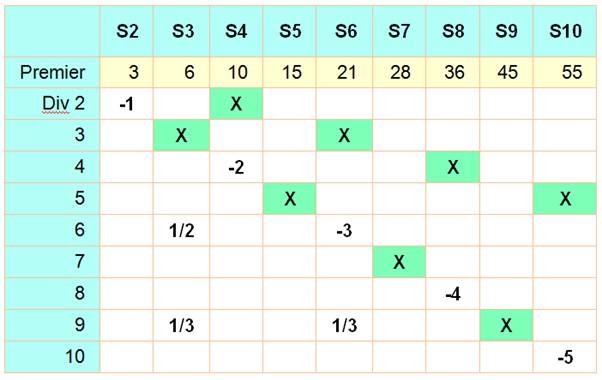
Somme de k nombres consécutifs à partir de n: c'est n fois le premier nombre plus des suppléments qui sont finalement la somme des entiers de 1 à k – 1 (le premier étant plus 0 et le dernier + k – 1).
Si k est impair > 1
Si k est pair > 2

Voir Brève 523

Bilan

La somme de n nombres consécutifs est divisible

par n pour n impair et

par n/2 pour n pair.

Suite	Nombres polis ou multisomme de consécutifs Entiers consécutifs en général Formes diverses Critères généraux Divisibilité – Index
Voir	Calcul mental – Index Fermat Produit de consécutifs – Factorielle tronquée Théorie des nombres – Index
DicoNombre	Nombre 100
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Decompos/aaaDIVIS/SomConse.htm