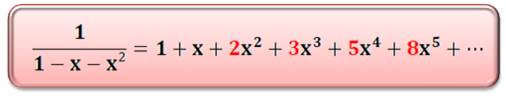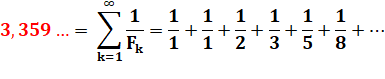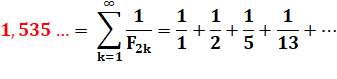|
|||||||||||||||||||||||||||||
![]()

|
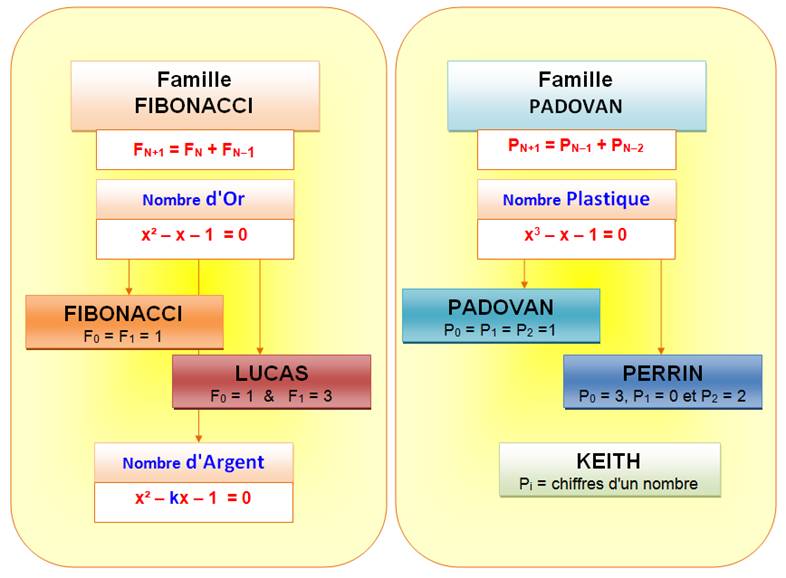
SUITE DE FIBONACCI
Suite
de nombres facile à construire. Et
pourtant, que de propriétés! Et,
surtout, suite très présente dans la nature … Suite
introduite1 par Fibonacci
de Pise (1170-1250), mathématicien qui a participé à l'introduction des nombres arabes (en provenance
d'Inde2) en Europe. Cette suite était connue des Indiens bien
avant lui, notamment de Hemchandra. Si
Fibonacci a compris l'importance de tels nombres, c'est qu'avant tout il
était marchand. Après lui, les étudiants qui utilisaient l'arithmétique
pratique, évitaient les universités et cherchaient des "maistres
d'algorisme". 1 C'est Édouard Lucas qui appela
cette liste de nombres: suite de Fibonacci". 2 Mathématiciens indiens: Gogala,
Pingala et Hemachandra. |
Anglais: Fibonacci numbers, series or
sequence
|
|
|
|
|
|
|
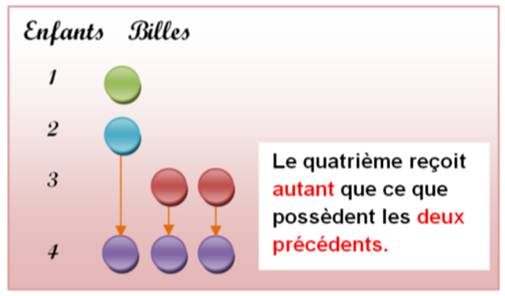
Attribution des
billes au 3e enfant
Attribution des
billes au 4e enfant
Attribution des
billes aux enfants suivants
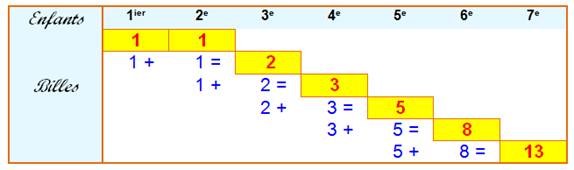
Note:
avec
cette méthode de construction, chaque colonne affiche le même nombre |
Voir Jeu
du remplissage du rectangle avec des dominos
La page sur
les lapins de Fibonacci constitue une bonne
introduction pour débutants.
|
|
||||||
|
Suite de
nombres dont chaque terme est la somme des deux
précédents: 0, 1, 1, 2, 3, 5, 8, 13, 21, … 11 / 23 ou
23 novembre: jour de Fibonacci (Fibonacci Day). Car la
suite de Fibonacci commence par: 1, 1, 2, 3,
…
Lecture: La suite de Fibonacci Fn
est la succession de tous les nombres de n = 1 à l'infini telle que les deux
premiers sont égaux à 1 et les suivants se calculent comme la somme des deux
précédents. Par convention, on pose que le nombre de Fibonacci de rang 0 est égal
à 0.
Voir Démonstration
par récurrence
|
||||||
|
|
||
|
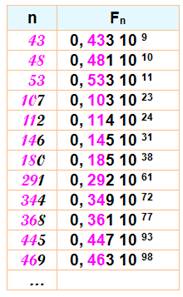
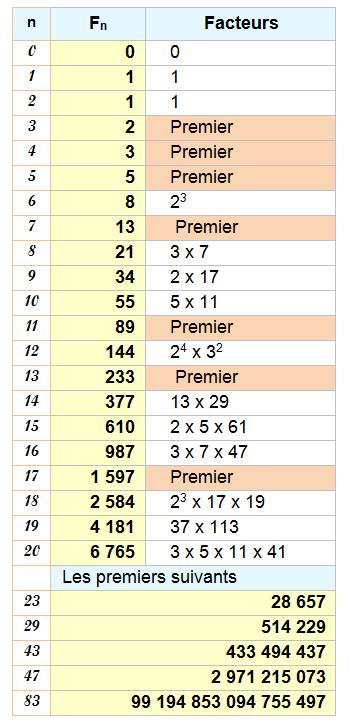
et les quelques Fibonacci premiers suivants.
Vérifié,
non prouvé. On ne sait pas s'il sont en nombre infini. La
réciproque n'est pas vraie: un rang premier n'est pas nécessairement associé
à un Fibonacci premier.
|
|
|
Voir Table des nombres de Fibonacci /
Production de ces valeurs
/ Formule
de Binet
|
Polynôme
générateur des nombres de Fibonacci
Voir Polynômes générateurs des
k-bonacci et programmation |
|
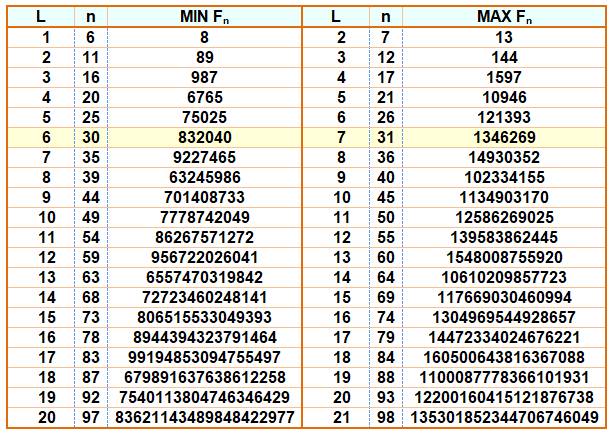
Les
plus petits et plus grands Fibonacci pour une longueur
donnée Exemple:
le plus
grand avec si chiffres est F30 = 832 040 Et le plus petit
à sept chiffres est F31 = 1 346 269
|
|
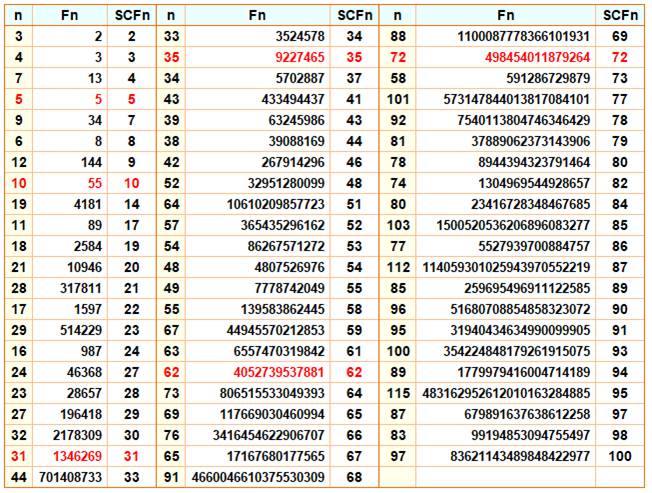
Somme
des chiffres des nombres de Fibonacci (SCFn) Exemple:
F10 = 55
et la somme des chiffres est 10. Classé
par somme croissance des premiers Fibonacci donnant une somme donnée. Exemple: F11 = 89, somme
17 et retenu, mais pas le suivant F17 = 377, somme 17.
En
rouge, la somme est égale au rang: SCFn
= n La suite est: 5, 10, 31, 35, 62, 72, 175,
180, 216, 251, 252, 360, 494, … La densité
moyenne des ses nombres est d'environ 0,208987 … |
|
Constante des inverses de Fibonacci (reciprocal
Fibonacci constant).
=
3,3598856662 4317755317 2011302918 9271796889 0513373196 8486495553
8153251303 1899668338 3615416216 45679 …
=
1,5353705088362529850... |
![]()
|
|
|||||||||||||||||||||||||||||
|
Général |
|
||||||||||||||||||||||||||||
|
Valeurs |
|
||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||
|
Propriétés |
|
||||||||||||||||||||||||||||
|
Cousins |
|
||||||||||||||||||||||||||||
|
Nombre d'or |
|
|
Liens particuliers |
|
|
|
||
|
|
||
|
|
||
|
Identique
à celle de Fibonacci mais telle que chaque terme est la somme du précédent et
deux fois celui d'avant. La
suite de Jacobsthal caractérise également la croissance d'une population de
lapins: un couple
de lapins donne naissance à deux nouveaux couples chaque mois et chaque
couple commence à engendrer à partir du deuxième mois suivant sa naissance. Liste 0,
1, 1, 3, 5, 11, 21, 43, 85, 171, 341, 683, 1365, 2731, 5461, 10923, 21845,
43691, 87381, 174763, 349525, 699051, 1398101, 2796203, 5592405, 11184811,
22369621, 44739243, 89478485, 178956971, 357913941, 715827883, 1431655765,
2863311531, 5726623061, … |
|
Dans
le roman Da Vinci Code de Dan Brown (205), on
retrouve la série de Fibonacci. Elle est utilisée comme code d'un coffre. Et,
aussi, en désordre, pour signifier qu'il y a erreur.
13
– 3 – 2 – 21 – 1 – 1 – 8 – 5 Diable
intraitable (draconina devil) Oh,
saint boiteux (Oh, lame saint) Langdon
relut le message et lève les yeux vers Fache. "
Que diable cela signifie-t-il? |
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Iteration/Fibonacc.htm |
![]()