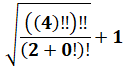|
|||||||||||||||||||||||||||||||||||||
![]()
|
Opérations avec les CHIFFRES de l'ANNÉE Puzzle classique qui consiste à former
tous les nombres de 0
à N en utilisant les chiffres
de l'année en cours et les opérations usuelles Par exemple avec l'année
2016, et
|
|
|
||
|
Chiffres et nombres licites Tous les chiffres de
l'année: pour 2016 => {0, 1, 2, 6) Et aussi tous les nombres
formés avec ses chiffres: 12, 16, 61, 126, 261 … Opérations autorisées
Procédé Former un nombre N donné en
utilisant une combinaison des opérations proposées. Les quatre chiffres de l'année
doivent tous être présents. |
Nature du résultat Plusieurs niveaux de
réussite
But Obtenir une expression pour
chacun des nombres de 0 à N avec N le plus grand possible: Nmax. Tableau Le tableau montre qu'il
existe au moins une expression pour tous les nombres de 0 à 50 pour les
années 2014, 2015 et 2016. Dans l'état de mes
recherches, Nmax avec chiffres dans l'ordre vaut 31 ou
32. |
|
![]()
Tableau pour N = 0 à 50
et pour les années 2014, 2015 et 2016
En bleu, les solutions avec chiffres dans l'ordre
|
|
2014 |
2015 |
2016 |
|
|
0 |
2 x 0 x 1 x
4 |
2 x 0 x 1 x
5 |
2 x 0 x 1 x
6 |
|
|
1 |
(2 + 0! +
1) / 4
20 x 1
x 4 20
x 14 4 – 2 – 1 + 0 |
20 x 1
x 5 2 x 0 x 5 + 1 (5 x 2) x 0 + 1 25 x 0 + 1 025 + 1 2150 |
20 x 1
x 6 etc. |
|
|
2 |
2 + 0 x 1 x
4
2 x 1 + 0 x 4 4!/2 – 10 |
–2 + 0 –1 +
5 2 + 0 x 1 x 5 015 + 2 |
–2 – 0! –1
+ 6 etc. |
|
|
3 |
2 x 0 – 1 +
4 –2 + 0 + 1
+ 4 |
2 + 0 + 15 20 / 5 – 1 10 – 5 – 2 |
–2 + 0 –1 +
6 1 + 2 + 0 x 6 |
|
|
4 |
2 x 0 x 1 +
4 |
–2 + 0 + 1
+ 5 20/5 x 1 |
–2 – 0! + 1
+ 6 20 – 16 |
|
|
5 |
2 + 0 – 1 +
4 20 x 1 / 4 (2 /0,1) /
4 4! – 20 + 1 |
( 20
)1 x 5 20 – 15 |
–2 + 0 + 1
+ 6 6 – 1 + 0 x 2 |
|
|
6 |
20
+ 1 + 4 20 -14 20 / 4 + 1 |
2 x 0 + 1 +
5 2 + 0 – 1 + 5 5! / 20 x 1 |
2 – 0! – 1
+ 6 6 + 0 x 1 x 2 |
|
|
7 |
2 + 0 + 1 +
4 14 / 2 + 0 |
20
+ 1 + 5 12 – 5 + 0
|
2 x 0 + 1 +
6 1 + 6 + 0 x 2 |
|
|
8 |
(2 + 0 x 1)
x 4 2 + 0! +1 +
4 1 x 2 x 4 + 0 |
2 + 0 + 1 +
5 (5 – 1) x 2 + 0 |
2 + 0! – 1
+ 6 2 + 6 + 0 x 1 |
|
|
9 |
2 x 0 + 1 +
4!! (2 + 0!)! –
1 + 4
|
(2 + 0) x 1
x 5 2 + 0! + 1 + 5 5 x 2 – 1 + 0 |
2 + 0 + 1 +
6 0 + 1 + 2 + 6 |
|
10 |
(2 + 0) x
(1 + 4) 2 + 0 x 1 +
4!! |
2 x (0! – 1
+ 5) 2 x 5 + 1 x 0 10 / 2 + 5 |
2 + 0! + 1
+ 6 2 x (0 – 1
+ 6) (6 – 1) x 2 + 0 |
|
11 |
2 + 0 + 1 +
4!! 4! / 2 – 1 + 0 |
–2 – 0! – 1
+ 5!! 2 x 5 + 1 + 0 (2 + 1)! + 5 + 0 |
(2 + 0!) –
1 + 6 10 / 2 + 6 2 x 6 – 1 x 0! |
|
12 |
(2 + 0 + 1)
* 4 10 – 2 + 4 12 – 4 x 0 |
2 x (0 + 1
+ 5) 15 – 2 – 0! |
(2
– 0! + 1) x 6 2
x (0 + 1) x 6 (2
+ 0!) x 12 + 0 x 6 |
|
13 |
–2 + 0 + (1
+ 4)!! 20 + 1 –
4!! |
–2 – 0 x 1
+ 5!! 15 – 2 + 0 |
–2 – 0 + (–
1+ 6)!! 2 x 6 + 1 x 0! |
|
14 |
20
x 14 –(2 x 0)! +
(1 + 4)!! 24 – 10 |
20 – 1 – 5 2 x (0! + 1 + 5) |
2 x (0 + 1
+ 6) (1 + 6) x 2 + 0 |
|
15 |
20
+ 14 20 – 1 – 4 42
– 1 + 0 |
(2
+ 0 + 1) x 5 25 – 10 52
– 10 |
2 x 0 + (–
1+ 6)!! 2 x (6 + 1) + 0! (6 – 1)!! + 2 x 0 |
|
16 |
(2
+ 0! + 1) x 4 201
– 4 2
+ 0 + 14 |
20
– 1 + 5 21 – 5 + 0 |
2 x (0! + 1
+ 6) 2 x 0 + 16 26 – 10 |
|
17 |
2
+ 0 + (1 + 4)!! 20
+ 1 – 4 |
2
+ 0! – 1 + 5!! 10 + 5 + 2 12 + 5 + 0 12 + 05 |
2 – 0 + (–
1+ 6)!! (6 – 1)!! + 2 x 0! |
|
18 |
(2
+ 0) x (1 + 4!!) 10 + 2 x 4 |
(2
+ 0!) x (1 + 5) 12 + 5 +
0! 5! – 102 10 / .5 –
2 |
(2
+ 0 + 1) x 6 2 + 0 + 16 10 + 6 + 2 |
|
19 |
–((2
+ 0!)! – 1) + 4! 20
– 14 40 – 21 |
20
– 15 (2 + 0! +
1)! – 5 |
20
– 16 10 + 6 + 2 + 0! |
|
20 |
(2
+0! + 1)! – 4 40 x 1 / 2 10 x 4 / 2 |
20
x 15 2 x 5 + 10 102
/ 5 5! – 102 |
20
x 16 120 / 6 |
|
21 |
–2
+ 0 – 1 + 4! 20 + 14 40 / 2 + 1 |
20
+ 15 –
(2 + 0!) + (–1 + 5)! |
20
+ 16 21 + 0 x 6 |
|
22 |
–2
+ 0 x 1 + 4! 24 – 1 –
0! |
25
– 10 |
(2 + 0!)! +
16 10 + 2 x 6 (6 – 2)! – 1 – 0! |
|
23 |
2
x 0 – 1 + 4! 20
– 1 + 4 10 / .4 –
2 |
–
20 + (–1 + 5)! 52
– 1 – 0! |
20
– 1 + 6 (6 – 2)! – 10 |
|
24 |
2
x 0 x 1 + 4! 20
x 1 + 4 24 x 1 + 0 10 x 2 + 4 |
20
– 1 + 5 25 – 01 50 / 2 –
1 |
(2
+ 0! + 1) x 6 (2
+ 0!)! x ((2
+ 0!)!)!! / (6 – 2)! + 1 x 0 |
|
25 |
20
x 1 + 4! 20
+ 1 + 4 102
/ 4 |
20
x 1 + 5 10 x 2 + 5 5 x 10 / 2 |
20
– 1 + 6 (6 – 1)2 +
0 (6 – 2)! + 10 |
|
26 |
2
+ 01 + 4! 24 + 0! +
1 42
+ 10 |
20
+ 1 + 5 25 +01 |
2 + (–0! –
1 + 6)! 10 x 2 + 6 (6 – 2)! + 1 + 0! |
|
27 |
2
+ 0 + 1 + 4! 20 + 4!! –
1 10 / .4 +
2 |
2
+ 0! + (–1 + 5)! 52
+ 1 + 0! 5!! + 0 +
12 |
20
+ 1 + 6 |
|
28 |
2
+ 0! + 1 + 4! (2
+ 0) x 14 40 - 12 |
20
+ (–1 + 5)!! 2 x (15 –
0!) |
– 20 + 1 x
6!! 6!! – 20 x 1 |
|
29 |
(2
+ 0!)! – 1 + 4! 14 x 2 +
0! 21 + 4!! +
0 |
(2
+ 0! + 1)! + 5 50 – 21 |
– 20 + 1 +
6!! 6!! – 20 + 1 6 / (.1 x 2) – 0! |
|
30 |
(2
+ 0 + 1)! + 4! 21 + 4!! +
0! 120 / 4 |
(2
+ 0 x 1) x 5!! 15 x 2 + 0 |
(2
+ 0! + 1)! + 6 (2
+ 0!)! x (–1+ 6) 6 / .2 + 1 x 0 |
|
(2
+ 0!)! + 1 + 4! 12 / .4 +
0! |
??? (2 + 0!)!
x 5 + 1 51 – 20 |
??? (6 – 1)!! x 2 +0! 6 / (.1 x 2) + 0! |
|
|
32 |
??? 24+1
+ 0 |
2
x (0! + 15) 25
+ 1 x 0 |
(2 + 0) x
16 6 / .2 + 1 + 0! 160 x .2 |
|
33 |
((2
+ 0!)!)!! – (1 + 4)!! 24+1
+ 0! |
25
+ 1 + 0 |
((2 +
0!)!)!! – (–1+6)!! 2 x 16 + 0! |
|
34 |
20
+ 14 |
25
+ 1 + 0! 5! x .2 +
10 |
2
x (0! + 16) 62 – 1 – 0!
|
|
35 |
20
+ (1 + 4)!! 40 – 1 /
.2 |
(5 + 1)2
– 0! |
62 – 1 + 0 (1 + 6) / .2 + 0 |
|
36 |
(2 + 1)! x
(4 – 0!)! 10 + 4! +
2 |
(5 + 1)2 + 0 (5 +
1)! / 20 |
20 + 16 26 + 10 (6 x 1)! / 20 |
|
37 |
40 – 2 – 1 0! + 12 +
4! |
(5 + 1)2 + 0! |
62 + 1 + 0 |
|
38 |
41 – (2 +
0!) 10 x 4 – 2
|
50 – 12 |
62 + 1 + 0! |
|
39 |
((2
+ 0!)!)!! – 1 – 4!! 41 – 2 + 0 |
5! / (2 +
1) – 0! 20 / .5 –
1 |
60 – 21 ((6 – 2) / .1 – 0! |
|
40 |
42 – 0! –
1 1 x 20 x |
5! / (2 +
1) + 0 10 / .25 |
20 x (6 – 1)! / (2 + 0!) ((6 – 2) / .1 + 0 |
|
41 |
((2
+ 0!)!)!! + 1 – 4!! 42 – 1 – 0
41 + 2 x 0 |
5! / (2 +
1) + 0! |
((2 + 0!)!)!!
– 1 – 6 61 – 20 ((6 – 2) / .1 + 0! |
|
42 |
10 x 4 + 2 42 x 1 + 0 20
+ 41 |
52 – 10 210 / 5 25
+ 10 |
– (2 + 0!)!
x 1 + 6!! |
|
43 |
20
– 1! + 4! 40 + 2 + 1 |
((2 +
1)!)!! – 5 + 0 21 / .5 +
0! |
((2 +
0!)!)!! + 1 – 6 |
|
44 |
20
x 1 + 4! 41 + 2 +
0! |
50 – (2 +
1)! (5 – 1)! +
20 |
–2 – 0! – 1
+ 6!! 6!! – 2 x (1 + 0!) 10 / .2 – 6 |
|
45 |
20
+ 1 + 4! |
(5 – 0!)!
+ 21 |
–2 + 0 – 1
+ 6!! 6!! – 2 – 1 – 0 |
|
46 |
((2
+ 0 + 1)!)!! – 40 + (2 +
1)! |
(5 + 1)!!
– 2 + 0 |
–2 + 0 x 1
+ 6!! 6!! – 2 + 1 – 0! |
|
47 |
((2
+ 0!)!)!! + 1 – 4! x 2 – 1
+ 0 |
50 – 2 – 1
|
2 x 0 – 1 +
6!! 6!! – 2 + 1 x 0! |
|
48 |
2!
x 0! x 1! x 4! (2
+ 0! + 1)! + 4! 12 x 4 + 0 |
2
x 0 + (1 + 5)!! 50 – 2 x 1 |
2 x 0 x 1 +
6!! (2 + 0!) x 16 60 – 12 6!! + 2 – 1 – 0! |
|
49 |
20
+ ((1 + 4! x 2 + 1
+ 0 20 / .4 –
1 |
(5 + 1)!!
+ 2 – 0! 50 – 2 + 1 |
2 x 0 + 1 +
6!! 6!! + 2 – 1 + 0 |
|
50 |
(20
/ .1 )/4 2 x (4! +
1) + 0 |
52
x (1 + 0!) (2 – 1) x
50 |
2 + 0 x 1 +
6!! 6!! + 2 + 1 x 0 |
Bilan
|
Évidemment,
le jeu continue après N = 50. Quel est le premier nombre sans réponse du
tout? Ce
tableau présente les solutions typiques sans les donner toutes. Certaines
solutions complémentaires sont données car dignes d'intérêt (comme 9 avec
2014). |
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Site |
|
|
Cette page |
![]()