NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 24/03/2025 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	CALCULS RAPIDES
Débutants Général	PUISSANCES			Glossaire Général
INDEX Calcul rapide Cubes	Carrés	Cubes	Racines
		Sommaire de cette page >>> Calcul rapide des cubes >>> Approche >>> Unités des cubes >>> Calcul des cubes >>> Écart entre cubes

CALCUL MENTAL

des CUBES des NOMBRES

Le paysage formé par la suite des cubes est plus complexe que celui des carrés. Néanmoins, on peut aussi y reconnaître quelques familiers. Le calcul mental des cubes et des racines cubiques des nombres nécessitent un bon entraînement préalable avec les carrés et les racines carrées. On pourra ensuite se remémorer la technique de calcul des racines cubiques à la main.

Calcul rapide des cubes		haut
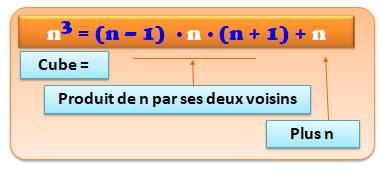
Méthode Pour calculer le cube du nombre n: multiplier n par ses deux voisins, et ajouter n. Justification Soit n et ses deux voisins (n – 1) et (n + 1). Le produit: (n – 1) n ( n + 1) = (n – 1) (n² + n) = n^3 + n² – n² – n = n^3 – n En isolant le cube: n^3 = (n – 1) n (n + 1) + n	En bref: Exemples de calculs 3^3 = 2 × 3 × 4 + 3 = 24 + 3 = 27 5^3 = 4 × 5 × 6 + 5 = 120 + 5 = 125 9^3 = 8 × 9 × 10 + 9 = 720 + 9 = 729 11^3 = 10 × 11 × 12 + 11 = 10 × 132 + 11 = 1331 21^3 = 20 × 21 × 22 + 21 = 20 × 462 + 21 = 9240 + 21 = 9261

Voir Brève 61-1219

APPROCHE

On connaît les cubes des chiffres

Ou, présentation plus classique

0^3 = 0 1^3 = 1 2^3 = 8 3^3 = 27 4^3 = 64 5^3 = 125 6^3 = 216 7^3 = 343 8^3 = 512 9^3 = 729

10^3 = 1 000 11^3 = 1 331 12^3 = 1 728 13^3 = 2 197 14^3 = 2 744 15^3 = 3 375 16^3 = 4 096 17^3 = 4 913 18^3 = 5 832 19^3 = 6 859 20^3 = 8 000

UNITÉS DES CUBES

Chiffre	1	2	3	4	5	6	7	8	9
Dernier chiffre du cube	1	8	7	4	5	6	3	2	9
Même position	ü			ü	ü				ü

Somme des chiffres symétriques égale à 10

comme pour les chiffres du départ,

avec la même position ou position symétrique.

Voir Unités des cubes / Tous les chiffres pour les unités des cubes

CALCUL DES CUBES

Identité utilisée

(A + B)³ = A³ + 3 A²B + 3 AB² + B³

Voir Identités remarquables

Avec les unités et les dizaines

n^3	=	(A + B)^3	=	A^3	+	3 A^2B	+	3 AB^2	+	B^3	=	N
11^3		(10 + 1)^3		1000		300		30		1		1331
12^3		(10 + 2)^3		1000		600		120		8		1728
12^3		(10 + 3)^3		1000		900		270		27		2197
21^3		(20 + 1)^3		8000		1200		60		1		9261
22^3		(20 + 2)^3		8000		2400		240		8		10648

Cas des nombres en 9

n^3

=

(A - B)^3

=

A^3

–

3 A^2B

+

3 AB^2

–

B^3

=

N

9^3

(10 – 1)^3

1000

300

30

1

729

19^3

(20 – 1)^3

8000

1200

60

1

6859

Par le double

n^3	=	(2A)^3	=	8A^3	=	N
12^3		(2 x 6)^3		6 x 216		1 728
16^3		(2 x 8)^3		8 x 512		4 096

ÉCART ENTRE CUBES

Observation

A^3	=	A^3
(A+1)^3	=	A^3+ 3A^2 + 3A + 1
Écart	=	3A (A+1) +1

Règle

Écart entre les cubes de deux nombres successifs égal

3 fois le produit des 2 nombres plus 1

Calcul par incrément

n^3	=	(n – 1)^3	+	E	=	N
10^3						1 000
11^3		10^3 1 000		3 x 10 x 11 + 1 330 + 1		1 331
12^3		11^3 1 331		3 x 11 x 12 + 1 396 + 1		1 728
13^3		12^3 1 728		3 x 12 x 13 + 1 468 + 1		2 197
14^3		13^3 2 197		3 x 13 x 14 + 1 546 + 1		2 744

Observation sur les écarts d'ordre 3

n	n^3	Écart	Écart 2	Écart 3
1	1
2	8	7
3	27	19	12
4	64	37	18	6
5	125	61	24	6
6	216	91	30	6
7	343	127	36	6
8	512	169	42	6
9	729	217	48	6
10	1 000	271	54	6
11	1 331	331	60	6
12	1 728	397	66	6
13	2 197	469	72	6
14	2 744	547	78	6
15	3 375	631	84	6

Suite	Calcul des racines Cubes – Index
Voir	Calcul Mental – Index Carrés et unités des puissances Unités des cubes
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Geometri/Cubecal.htm