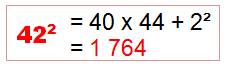|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
CALCUL
des CARRÉS
|
Bon à savoir
|
Le carré d'un nombre à n chiffres aura 2n – 1 ou
2n chiffres (11² = 121, … 31² = 961, 32² = 1024,
… et 99² = 9801). Les nombres à partir desquels le carré prend un
chiffre de plus pour n avec le même
nombre de chiffres : [32, 1024], [317,
100489], [3163, 10004569], [31623, 1000014129], [316228, 100000147984] Un carré à k chiffres est le carré d'un nombre à
k/2 chiffres si k est pair et 1/2 (k + 1) chiffres si k est impair. |
|
|
||
|
Cas
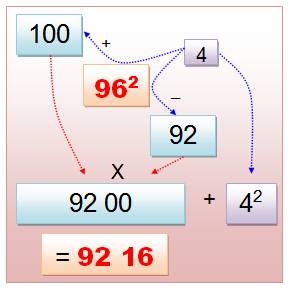
général Exemple 96² = 100 x 92 + 4² =
9216 Procédé:
ajouter 4 pour arriver à 100 et les retrancher (92); faire le produit des
deux (9200) et ajouter le carré de l'écart (4² = 16). Propriété:
(a + d)(a
– d) + d² = a² Autre
exemple:
Suite
>>> |
|
|
|
Cas
simple Exemple Je ne me souviens plus
du carré de 7; J'hésite! Procédé:
prendre les deux nombres autour de 7, les multiplier et ajoutez 1: Propriété:
(a + 1)(a
– 1) + 1 = a² |
7² = 6 x 8 + 1 = 48 + 1
= 49 101² = 100 x 102 + 1 = 10 200
+ 1 = 10 201 |
|
Voir Calcul
mental – Index / Table de multiplication / Identités remarquables
|
|
|||||
|
Notations |
N = 10d + u d' et u' compléments à 10 |
26 = 2 x 10 + 6 d' = 8 et u' = 4 |
|||
|
Cas général |
|||||
|
(10d +
u)² =100d² +
u² + 20du |
|
19² 23² 46² 99² |
|||
|
En + Propriété: a² =
(a-b)(a+b) + b² |
|
11² 15² 42² 101² 122² |
|||
|
En – |
|
19² 17² 48² 99² 119² |
|||
|
Trucs associés |
|||||
|
Calcul de produits Propriété: (a-b)(a+b)
= a² – b² |
N x M avec N = 10d + u
et M = 10d – u |
23 x 17 = 20² – 3² = 391 55 x 65 = 60² – 5² = 3 575 115 x 85 = 100² – 15² = 10 000 – 225
= 19 885 |
|||
|
Petits trucs en plus, amusants! |
||
|
Nombres en
…5 |
N² = d x (d+1), puis 25 |
35² 105² |
|
Nombres en
…1 |
D² + 2D + 1 avec D dizaine
inférieure |
21² = 20² + 40 + 1 = 441 71² = 70² + 140 + 1 = 5
041 131² = 130² + 260 + 1 =16 900 + 260 + 1 = 17 161 |
|
Nombres en
…9 |
D² – 2D + 1 avec D dizaine
supérieure |
19² = 20² – 40 + 1 = 361 59² = 60² – 120 + 1 = 3
481 119² = 120² – 240 + 1 = 14 400 – 240 + 1 = 14 361 |
|
Nombres
autour de 50 Propriété (50+R)² = 2500+100R+R² |
25 + R, puis R² (2 chiffres) Avec R =
différence à 50 |
52² 57² 49² 42² |
|
Nombre
suivant |
(N+1)² = N² + 2N + 1 |
101² = 10 000 + 201 = 10
201 |
|
Nombre
précédent |
(N+1)² = N² – 2N +1 |
99² = 10 000 – 200 + 1 =
9 801 |
|
Règles particulières (pour la curiosité; les deux règles ci-dessus
suffisent) |
||
|
Nombres |
N² = N + u, puis u² (2 chiffres) |
102 105² |
|
Nombres |
N² = N – u', puis u'² (2 chiffres) |
98² 97² |
|
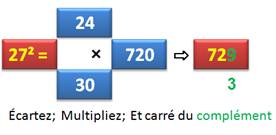
Nombres Propriété sur exemple 27² = (30 + 3)² = 30² +2x3x60 + 3² = 30(30-6) + 3² = 30x24 + 3² |
N² = Dx(10D + 2u'), puis u'² |
22² 62² 33² 106² |
|
Nombres |
N² = Dx(10D – 2u'), puis u'² |
18² 58² 27² 98² |
![]()
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
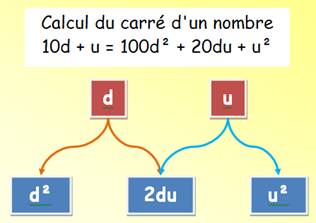
Nous décomposons le nombre en dizaines et unités et nous utilisons les identités remarquables pour calculer le
carré. Formule N = 10d + u N² = (10d + u)² = 100d² + 20du + u² Exemple 23² = 4 x 100 + 20 x 2 x 3 + 9 = 400 + 120 + 9 = 529 Procédé Pour obtenir les chiffres du carré: concaténez
le carré des dizaines et celui des unités pour former un nombre à quatre
chiffres. Ajoutez deux fois le produit
dizaines-unités en tant que dizaines. Attention à la propagation des retenues!
|
Illustration
Exemples de calcul 53² = 2
809
88² = 7
744
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Surtout, si on connaît le carré d'un groupe de
chiffres, comme: 25² = 625 12² = 144 |
125² = (100 + 25)² = 10 000 + 2 x 100 x 25 + 625 = 15 625 212² = (200 + 12)² = 40 000 + 2 x 200 x 12 + 144 = 44 944 888² = (800 + 88)² = 640
000 + 2 x 800 x 88 + 7744 = 788
544 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Voir Unités des carrés
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Remarquez: 58 = 60 – 2 = 60 – (8 – 2) 2 est le
complément à 10 de 8. Noté u' Formule N = 10d + u = 10(d+1) – u' N² = 100(d+1)² Exemple 28² = 100 x 9 – 20x3x2 + 2² = 900 – 120 + 4 = 784 Procédé Pour obtenir les chiffres du carré: faire
les opérations indiquées ci-dessous:
|
Exemples de calcul 29² = 841
77² = 5
929
98² = 9
604
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
Procédé La méthode alternative consiste à visualiser un
rectangle dont les dimensions sont simplement:
Le carré de N est le produit de ces deux nombres
plus u². Exemples 12² = 10 x 14 +
4 = 144 23² = 20 x 26 +
9 = 529 34² = 30 x 38 + 16 = 1 156 45² = 40 x 50 + 25 = 2 025 56² = 50 x 62 + 36 = 3 136 67² = 60 x 74 + 49 = 4 489 78² = 70 x 86 + 64 = 6 084 89² = 80 x 98 + 81 = 7 921 91² = 90 x 92 +
1 = 8 281 |
|
Voir Calcul des racines qui fait aussi
appel à ce type de représentation géométrique
Ce que nous avons appris
|
Nous savons calculer le carré d'un nombre
à deux chiffres selon trois méthodes, par ordre de facilité croissante:
Cependant, même la dernière méthode reste
encore ardue pour un calcul de tête. Les pages suivantes abordent les
tactiques particulières pour faciliter le calcul selon les chiffres des
unités ou des dizaines. |
|
|
|||||||||||||||||||||||||||||||||
|
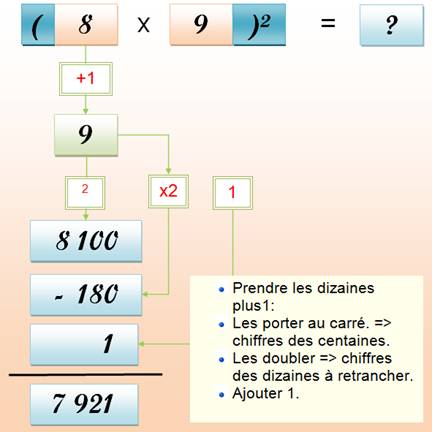
Un nombre terminé par 9 est égal à la dizaine
supérieure moins 1. Son carré est alors très facile à calculer. Exemple:
29 = 30 – 1 = (a – 1)
Méthode
|
|||||||||||||||||||||||||||||||||
Voir Suite et exemples
![]()
Nombre à trois chiffres
et plus
|
|
||||
|
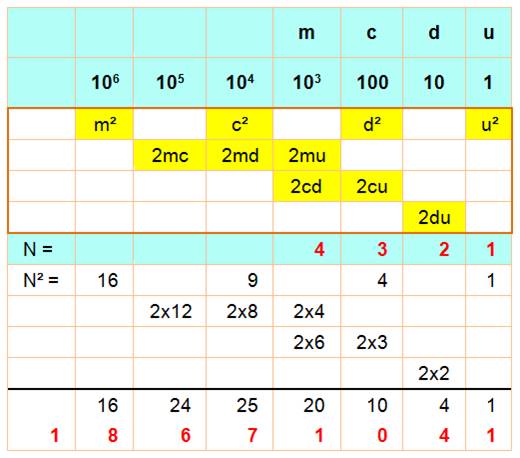
On isole chacun des chiffres: m milliers, c centaines,
d dizaines et u unités. On procède au calcul des termes dans les cases jaunes:
les carrés des chiffres et le double des produits deux à deux. On additionne dans chaque colonne en propageant la
retenue éventuelle. L'exemple donne: 4321² = 18 671 041 |
Tableau pour quatre
chiffres
|
|||
|
Identité utilisée |
(1000 m + 100 c +
10 d +
u )² = |
|
||
|
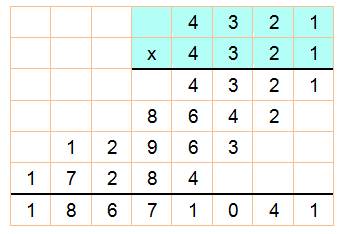
Comparaison avec la méthode de multiplication
habituelle. La méthode par multiplication posée a l'avantage d'être
universelle. La méthode par identité
remarquable est plaisante, mais ne remplacera pas la bonne vieille
méthode apprise à l'école. |
|
|||
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()