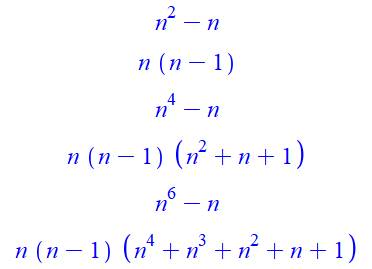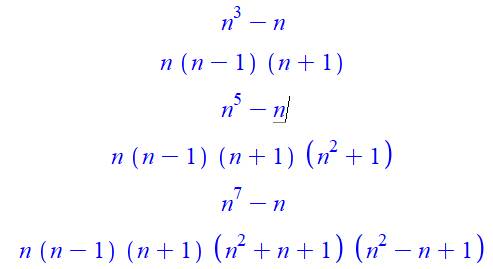NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 05/11/2017 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	Algèbre
Débutants Algèbre	IDENTITÉS			Glossaire Algèbre
INDEX Identités Algèbre	Remarquables	Degré > 2	Spéciales	Divers
	Inverses	a^n – b^n	a^n – 1	Complexes
	Puissances	Puissance 5	(x+ x² + …) ^k	Trigonométrie
	Newton	Euler & Riemann	Héron	Moivre
		Sommaire de cette page >>> Identités x^n – 1 >>> Identités n^k – n (puissance – nombre)

IDENTITÉS Spéciales Cas de: a^n – 1
Ce polynôme est toujours divisible par n – 1. 10^3 – 1 = 999 = 9 x 111 5^5 – 1 = 3 124 = 781	La factorisation produit un polynôme somme de puissances successives. Si a est une base de numération, a^n – 1 est converti en un repdigit de base a – 1. 3^4 – 1 = 80 = (3 – 1) x (3^3 + 3^2 + 3 + 1) = 2 x 11113 = 22223

IDENTITÉS – Factorisation maximale de xⁿ – 1

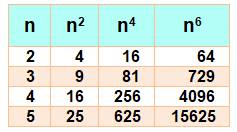
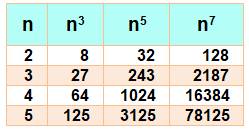
Tableau avec valeur de n puis factorisation de xⁿ – 1

Exemple pour n = 3 => x³ – 1 = (x – 1) ( x² + x + 1)

(le point est bien le signe multiplier)

1	(x – 1)
2	(x – 1) • (x + 1)
3	(x – 1)	• (x^2 + x + 1)
4	(x – 1) • (x + 1)	• (x^2 + 1)
5	(x – 1)	• (x^4 + x^3 + x^2 + x + 1)
6	(x – 1) • (x + 1)	• (x^2 + x + 1) • (x^2 – x + 1)
7	(x – 1)	• (x^6 + x^5 + x^4 + x^3 + x^2+ x + 1)
8	(x – 1) • (x + 1)	• (x^2 + 1) • (x^4+ 1)
9	(x – 1)	• (x^2 + x + 1) • (x^6 + x^3 + 1)
10	(x – 1) • (x + 1)	• (x^4 + x^3 + x^2 + x + 1) • (x^4 – x^3 + x^2 – x + 1)
11	(x – 1)	• (1 + x^10 + x^9+ x^8 + x^7 + x^6 + x^5 + x^4 + x^3 + x^2 + x)
12	(x – 1) • (x + 1)	• (x^2 + x + 1) • (x^2 – x + 1) • (x^2 + 1) • (x^4 – x^2 + 1)
13	(x – 1)	• (1 + x^12 + x^11 + x^10 + x^9 + x^8 + x^7 + x^6 + x^5 + x^4 + x^3 + x^2 + x)
14	(x – 1) • (x + 1)	• (x^6 + x^5 + x^4 + x^3 + x^2 + x + 1) • (1 – x + x^2 – x^3 + x^4 – x^5 + x^6)
15	(x – 1)	• (x^4+ x^3 + x^2 + x + 1) • (x^2 + x + 1) • (1 – x + x^3 – x^4 + x^5 – x^7 + x^8)
16	(x – 1) • (x + 1)	• (x^2 + 1) • (x^4 + 1) • (x^8 + 1)
17	(x – 1)	• (1 + x^16 + x^15 + x^14 + x^13 + x^12 + x^11 + x^10 + x^9 + x^8 + x^7 + x^6 + x^5 + x^4 + x^3 + x^2 + x)
18	(x – 1) • (x + 1)	• (x^2 + x + 1) • (x^6 + x^3 + 1) • (x^2 – x + 1) • (x^6 – x^3 + 1)
19	(x – 1)	• (1 + x^18 + x^17 + x^16 + x^15 + x^14 + x^13 + x^12 + x^11 + x^10 + x^9 + x^8 + x^7 + x^6 + x^5 + x^4 + x^3 + x^2 + x)
20	(x – 1) • (x + 1)	• (x^4 + x^3 + x^2 + x + 1) • (x^4 – x^3 + x^2 – x + 1) • (x^2 + 1) • (x^8 – x^6 + x^4– x^2 + 1)

Cas de n^k – n = n (n^k^– 1 – 1)
Il s'agit, bien entendu, des mêmes relations que celles vues ci-dessus, multipliée par n. Intérêt: propriétés de la différence entre nombre et sa puissance k. Un nombre et ses puissances sont de même parité. Tous les développements comprennent les facteurs n (n – 1), deux nombres consécutifs; le produit est divisible par 2 Un nombre diffère de sa puissance impaire par un multiple de 6. Tous les développements comprennent les facteurs (n – 1) n (n + 1), trois nombres consécutifs; le produit est divisible par 6. Ex: 27 – 3 = 24 = 6 x 4 / 243 – 3 = 240 = 6 x 40 / 2187 – 3 = 2184 = 6 x 364
Pair
Impair

Voir Cubes / Nombres somme de cubes (Taxicab) / Divisibilité

Retour	Identités
Suite	Identités pour degré supérieur à 2 Somme des entiers, des carrés, des inverses… Identités fractions Identités trigonométriques Identités nombres complexes Identités entre puissances Utilisation pour calcul de puissances complexes
Voir	Application aux multiplications Identité de Lagrange Identités trigonométriques Pépites Somme des entiers, des carrés…
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Identite/P2nm1.htm