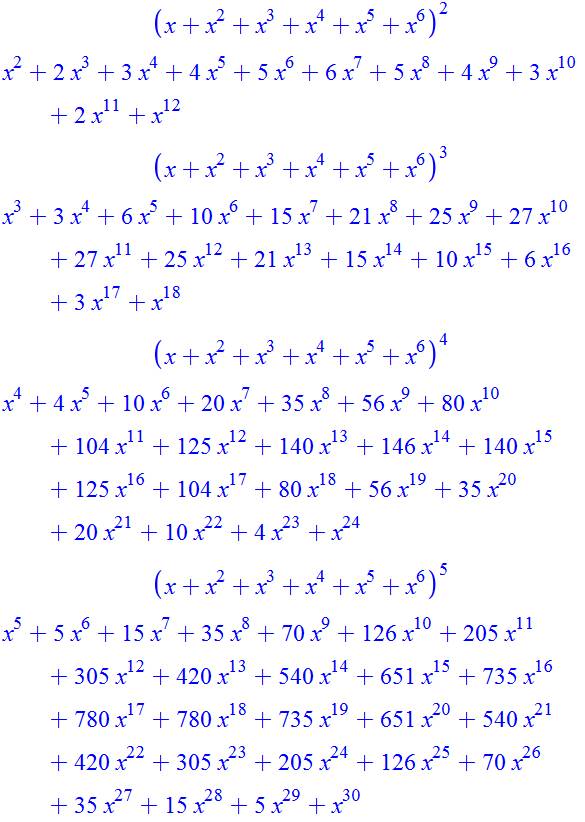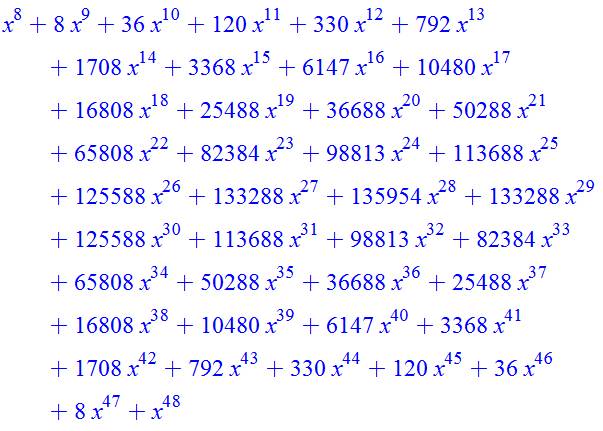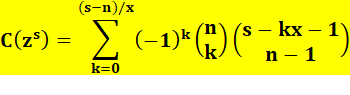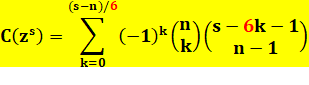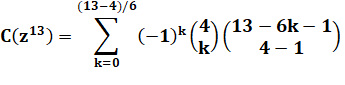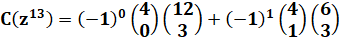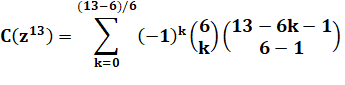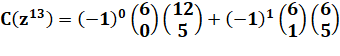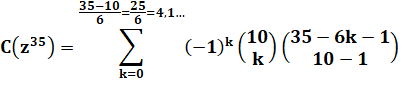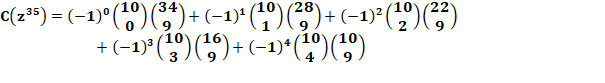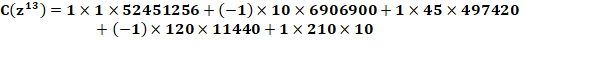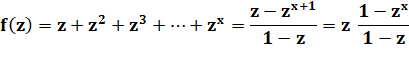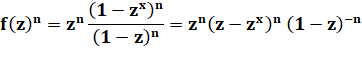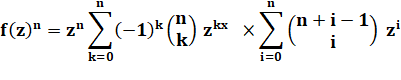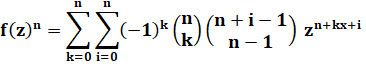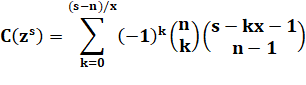|
|||||||||||||||||||||||||||||||||
![]()
|
Identités remarquables spéciales (x + x2 + x3
+…)k Polynôme
générateur permettant le calcul des quantités de partitions
ou encore la quantité de somme obtenues en lançant n dés possédant k faces
(usuellement 6). Exemples: avec trois dès,
la somme 13 est obtenue 21 fois. La lecture est simple: c'est le coefficient
de x13 dans le développement de la puissance 3 de ce polynôme (voir ci-dessous). Avec cinq dès, la somme 10 est obtenue 126 fois (tableau plus bas). |

Voir Même
sujet mais sous forme de table
|
|
|
|
Les coefficients donnent:
|
|
![]()
Méthode de calcul** (notions avancées)
|
|
|||
|
Formule générale pour n dès à x
faces, Valeur du
coefficient pour le degré ou la somme s. |
avec les
valeurs entières de k de 0 à (s – n) / x |
||
|
Cas du dé à 6 faces (x = 6) |
|
||
|
Exemple 1: Avec
quatre dés la somme 13 est possible
140 fois avec le dé classique à 6
faces. |
|
||
|
Exemple 2: Avec six
dés la somme 13 est possible 756 fois
avec le dé classique à 6 faces. |
|
||
|
Exemple 3: Avec dix
dés la somme 35 est possible 4 395 456
fois avec le dé classique à 6 faces. |
|
||
|
|
||
|
Fraction
correspondant au développement |
|
|
|
|
||
|
Retour
aux développements |
|
|
|
Mie en
commun des sommes |
|
|
|
Valeur de
chaque coefficient |
|
|
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Identite/Identxx2.htm
|
![]()