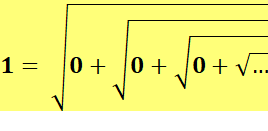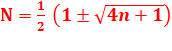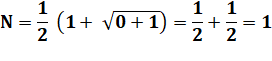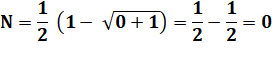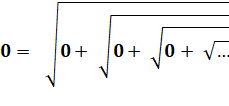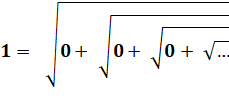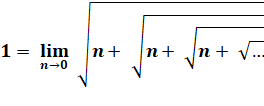|
|||||||||||||||||||||||||||
![]()
|
RACINES CONTINUES et ZÉRO Comment faire quelque chose
avec rien? Pour une fois le 0, peut ne
pas rester à 0!
|
|
|
|
|
Tout nombre entier N
est exprimable sous forme d'une racine continue dont la valeur sous le
radical est égale à: n = N² – N avec Mais, que se
passe-t-il pour n = 0 ?
|
|
|
|
||
|
|
|
|
|
|
Solution qui semble bien
naturelle. Des racines de 0 qui donnent
0. |
|
|
|
Solution possible également,
même si elle semble paradoxale. Elle se dessine par un
passage aux limites. Il faut partir d'un nombre
très petit et le diminuer progressivement. |
|
|
|
||
|
Formulation précise:
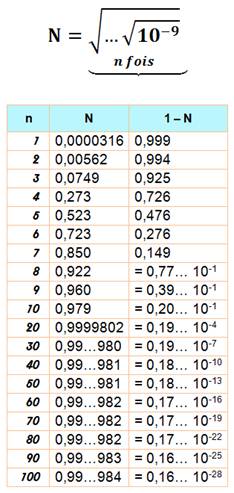
Plus n est petit et plus la
quantité de racines est grande et plus la valeur se rapproche de 1.
En prenant, non pas une
petite valeur, mais zéro précisément, la valeur reste à 0. |
Exemple de calcul
|
|
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
![]()