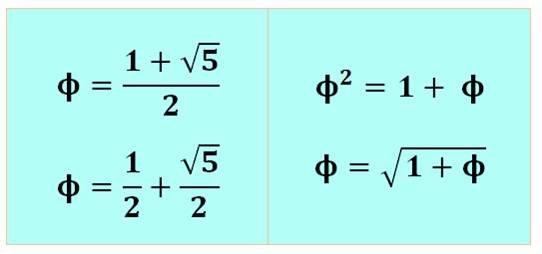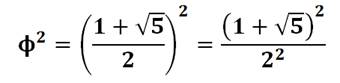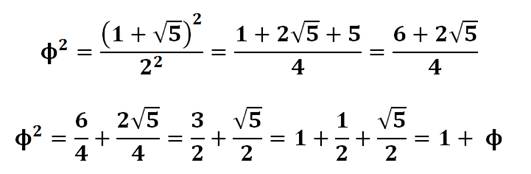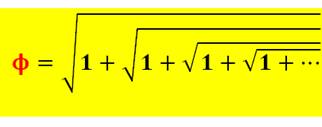|
|||||||||||||||||||||||||||
![]()
|
RACINES CONTINUES et NOMBRE D'OR Magie: transformation du 1 en or!
|
|
|
|
|
Problème
posé en classe de troisième Calculer la
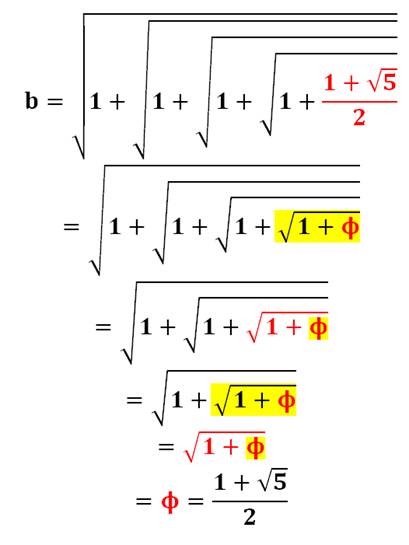
valeur de b
Réponse
Sa valeur et la propriété de son carré:
Explications: Le nombre d'or (Phi) est la solution de l'équation: x² – x – 1 = 0 Quant à son carré, il se calcule facilement:
Avec le développement
du carré: (a + b)² = a² + 2ab + b²
2) Avec cela, on simplifie progressivement l'expression Ensuite, en
remplaçant racine de (1+ Phi) par Phi: (les rouges se correspondent et les jaunes
aussi, alternativement)
|
|
|
|
||
|
|
|
|
|
|
|
|
|
Écart = 0, 000 001 666 |
|
|
|
Tout nombre entier N est exprimable sous forme d'une
racine continue dont la valeur sous le radical est égale à n = N² - N |
Voir Ramanujan
/ Racines continues
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()