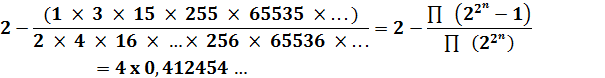|
|||||||||||||||||||||||||||||||||||
![]()
|
Thue-Morse ou Prouhet-Thue-Morse Suite, nombre, constante Suites binaires aux propriétés
particulières de non répétitivité. Cette
suite est connue sous le nom de Thue-Morse. C'est
pourtant Eugène Prouhet (1817-1867) qui l'utilise
en 1851 en combinatoire. Axel Thue (1863-1922) la redécouvre en 1912; de même que
Marston Morse (1892-1977) en 1921. |
Anglais: Thue-Morse sequence , also called
the Thue-Morse infinite word.
Voir Mathématiciens
des années 1800
|
Anglais: The fairest sharing sequence
La
suite PIIP IPPI est
identique à celle en ABBA BAAB. |
|
|
||||
|
Binaire |
Décimal |
Décimal * pour 0, binaire |
||
|
Démarrer
avec le 0 |
0 |
0 |
0 |
|
|
Concaténer
avec le complément binaire |
0 1 |
1 |
0,25 |
|
|
Recommencer
avec le nombre obtenu |
01 10 |
6 |
0,375 |
|
|
Encore … |
0110 1001 |
105 |
0,4101562500 |
|
|
Notez: ce premier nombre
binaire est palindrome. Mais, le suivant ne l'est pas. |
01101001 10010110 |
27 030 |
0,4124450684 |
|
|
0110100110010110 1001011001101001 |
1 771 476 585 |
0,4124540335 |
||
* Voir Explication de la
dernière colonne
|
|
||
|
Suite binaire dans laquelle on ne
trouve jamais trois fois de suite la même séquence. Pas trois 0, pas trois
01, pas trois 0011, etc. Suite classique de Thue-Morse … 0110100110010110 1001011001101001 … |
Cette
suite a été construite dans le cadre de la recherche de suites totalement désordonnées. Celle-ci
l'est dans sa forme, pas dans sa construction. La construction étant
d'ailleurs merveilleusement simple! => Faible
complexité algorithmique |
|
|
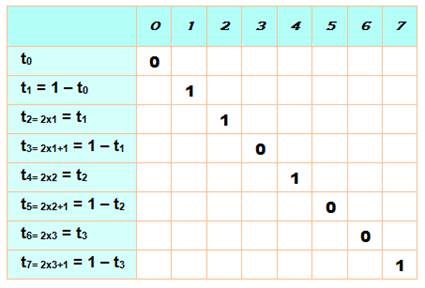
Définition alternative La suite peut être définie par la
relation de récurrence suivante:
La dernière relation étant relative
à du binaire, elle peut aussi s'écrire: |
Exemple avec huit itérations
|
|
|
|
||||||||||||||||||
|
Méthode 1 : Remplacement |
|
|||||||||||||||||
|
Méthode 2 : Complément |
|
|||||||||||||||||
|
Méthode 3 : Comptage binaire |
|
|||||||||||||||||
|
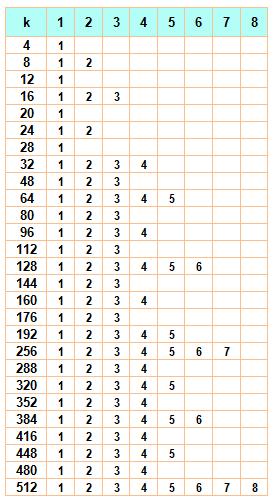
Méthode 4 : Construction rapide (copier – coller) |
On remplace les 0
et 1 par des dessins plus facile à visualiser
|
|||||||||||||||||
Construction rapide jusqu'à la 7e
génération
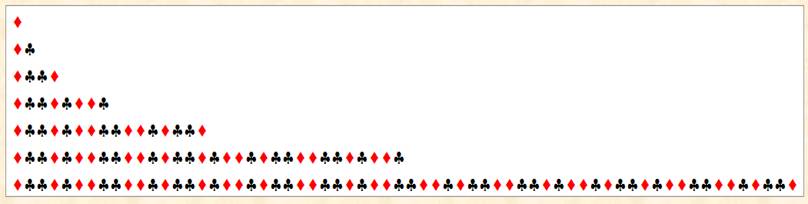
Voir Nombre
0110
|
|
||||||||||
|
La taille de la séquence grandit très, très vite. Cette suite ne présente aucune
périodicité:
|
Elle est autosimilaire
|
|||||||||
Voir Autosimilarité
et fractales
|
|
||
|
Autre tentative pour chercher à remplir les conditions de la
définition Chercher un nombre transcendant,
ne comportant pas de séquences répétitives comme |
Exemple
Les deux plus connus sont la constante "pi" et "e"
(exponentielle) Là aussi, échec car il y a un
contre-exemple de nombres transcendants
dont la règle de construction est simple. Donc, la suite n'est pas
désordonnée. Construction d'un transcendant Placez un 0 entre deux 1, puis deux
0 entre deux 1, puis quatre, etc. 010100100001000000001 Liouville
montra que ce nombre est transcendant en 1844, bien avant que soit démontrée
la transcendance
de pi ou e. |
|
|
|
||||||
|
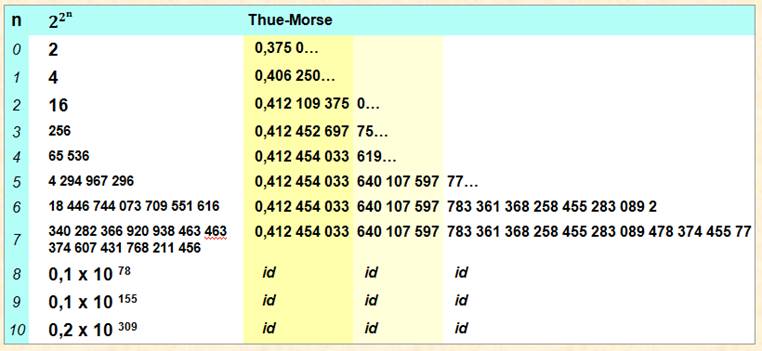
Le nombre
binaire (B) formé selon la méthode Thue-Morse est
prolongé jusqu'à l'infini. On le
transforme en une fraction en le précédent par 0,B Puis ce
nombre binaire est converti en décimal
|
|
|||||
|
Calcul
|
||||||
|
Début du calcul (15 itérations)
|
||||||
Voir Nombre
0,412 …
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
![]()