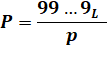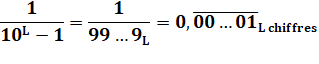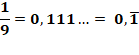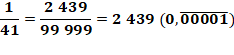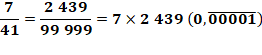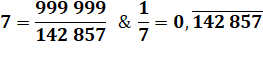|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
NOMBRES PÉRIODIQUES Longueur
de la période Une fraction; son
développement décimal périodique; quelle est la longueur de la période? |
Voir Cartographie
des nombres périodiques
|
|
||
|
Soit le
développement décimal de la fraction 1/p. La longueur maximale de la période
est égale à p – 1. La
longueur est égale à la valeur maximale ou un sous-multiple. |
|
|
|
La
longueur de la période L est déterminée par la plus petite valeur telle que:
Calcul de la période P
|
Pour p = 7
La période est de 6 chiffres P = 999 999 / 7 = 142 857 |
|
|
|
||
|
Formule de base |
|
|
|
Quel est le développement décimal
de 7/41? On trouve
que:
|
|
|
|
|
|||||||||||||||||
|
|
Soit la
division de a par b: il existe b types de restes possibles: ce sont toutes
les valeurs de 0 à b – 1. Exemple: pour la division par 3, les restes possibles sont: 0, 1 et 2.
La division et la relation
Q est la partie
entière du quotient et q1 est la première décimale.
La deuxième
décimale. Etc. Le développement périodique de la fraction a/b comporte, au plus, b – 1 décimales. |
||||||||||||||||
Voir Exemple de la division par 7 / Division posée
|
|
||
|
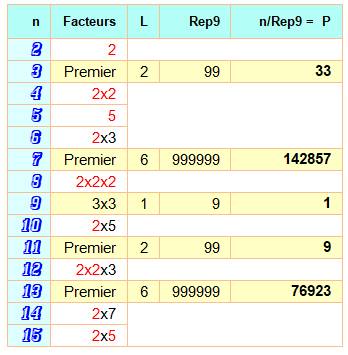
Tout nombre
n, non divisible par 2 ou 5, divise un
repdigit en 9 (R9) de q chiffres. Le
tableau montre cet effet pour les nombres de 2 à 15.
|
|
|
|
|
Programme On fixe la recherche au
25 premiers nombres (nmax), par exemple. Boucle examinant n pour toutes les valeurs de 2 à
nmax Si n n'est pas divisible par 2 (mod) et pas par 5 alors recherche du premier repdigit en 9 qui est
divisible par n. R est le repdigit en 9 qui grandit en ajoutant un
9 à chaque itération. Si le nouveau R est divisible par n, on
affiche le nombre n, la longueur du nombre
en 9 et la division R/n qui est la période (partie répétitive) de ce nombre
périodique. Ayant trouvé la divisibilité (R mod n = 0), on
force la fin de boucle en imposant: i = nmax. L'exécution du programme produit les nombres en bleu.
Par exemple avec 7, il faut attendre le repdigit avec six 9 (L = 6):
|
|
|
Quel est
le développement décimal de 7/41 On trouve
que 41 divise 99 999 et que 99 999 / 41 = 2 439 |
|
|
|
|
||
|
Théorème Pour tout nombre
n > 1, tel que PGCD(10, n) = 1, il existe un
nombre entier m (m < n) tel
que: Rappel de la relation en les
repdigits et les puissances de 10. 1000 – 1 = 999 10k – 1 = 99…9k |
Démonstration PGCD (10,
n) = 1 PGCD (10r , n) = 1 Aucun des
nombres 10, 102, .. 10n n'est
divisible par n Comme il
n'y a que n – 1 restes possibles, il en existe deux identiques:
Or PGCD(10v , n) = 1 Il reste
|
|
![]()
Graphe
montrant la longueur de la période pour 1/n jusqu'à n = 90
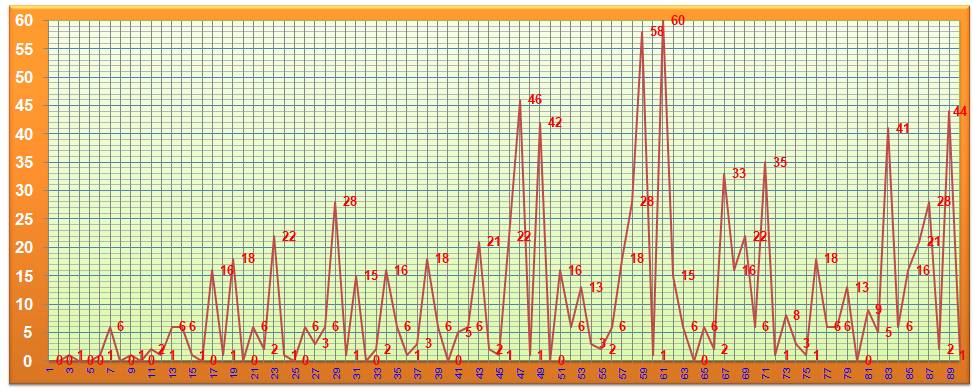
Valeurs numériques en commençant par n
= 1; les groupes en jaunes commencent par n = 1, 20, 40, 60 et 80
[
0, 0, 1, 0, 0, 1, 6, 0, 1, 0, 2, 1,
6, 6, 1, 0, 16, 1, 18,
0, 6, 2, 22, 1,
0, 6, 3, 6, 28, 1, 15, 0, 2, 16, 6, 1, 3, 18, 6,
0, 5, 6, 21, 2,
1, 22, 46, 1, 42, 0, 16, 6, 13, 3, 2, 6, 18, 28, 58,
1, 60, 15, 6, 0, 6, 2,
33, 16, 22,
6, 35, 1, 8, 3, 1, 18, 6, 6, 13,
0, 9, 5, 41, 6,
16, 21, 28, 2, 44, 1]
Voir Calcul de
la période et de sa longueur – Programmation
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
Site |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Nombre/aaaCycli/NbCycLon.htm |
![]()