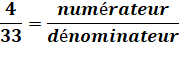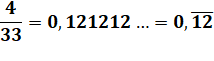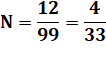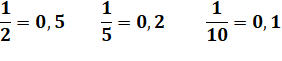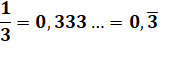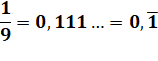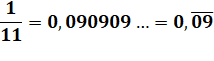|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
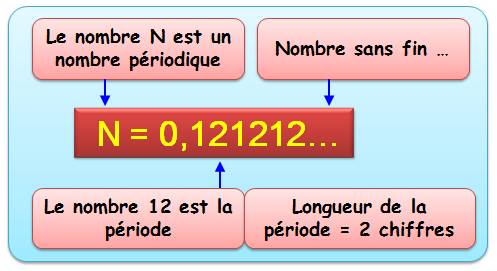
NOMBRES PÉRIODIQUES Approche
pour débutants Un nombre
périodique typique: 0,121212 … Les deux chiffres 1 et 2 se répètent sans fin
(c'est ce que signifient les points de suspension).
|
|
|
||
|
Nous
connaissons la fraction
(par exemple): Qui veut dire: quatre parts d'une tarte divisée en trente-trois
parts. |
|
|
|
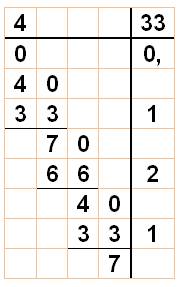
Ce n'est
jamais qu'une division
que, d'ailleurs, nous pouvons calculer. Le
quotient est un nombre qui commence par 0,12, puis les mêmes nombres
reviennent pour finalement donner un quotient égal à: |
|
|
|
Le nombre obtenu en effectuant la division est la traduction de la fraction en un
nombre avec une virgule. C'est le développement
décimal de la fraction. Le nombre
qui se répète est appelé la période. On le
note en le surlignant par une barre horizontale. Le nombre
0,121212… est un nombre périodique. |
|
|
|
Un truc amusant pour retrouver
la fraction: on multiplie par 100 et on soustrait: 100N – N = 99N … De
l'autre côté des égalités: la partie derrière la virgule est la même et la
différence pour cette partie après la virgule est nulle. La différence entre
les deux nombres complets est simplement égale à 12. En
divisant de chaque côté par 99, puis en simplifiant (division par 3 au
numérateur et au dénominateur), on retrouve notre fraction. |
|
|
|
|
||
|
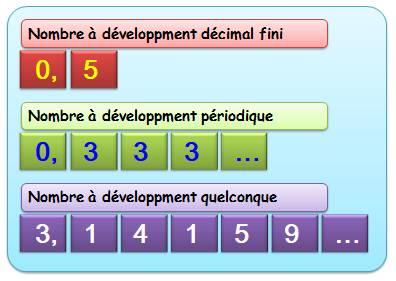
Il en
existe de trois types selon le comportement des chiffres après la virgule:
|
||
|
Nombres à quantité fixe de
décimales – Non-périodiques Les plus
simples sont ceux qui "tombent juste". Il y a une quantité fixe de
chiffres après la virgule |
|
|
|
Nombres à quantité infinie de
décimales – Périodiques Ceux qui nous
intéressent ici sont périodiques. |
|
|
|
Nombres à quantité infinie de
décimales – Non-périodiques (quelconque) Il
existe, enfin, des nombres avec des chiffres derrière la virgule qui ne se
répètent jamais. Ces chiffres semblent être placés les uns derrière les
autres au hasard. |
|
|
|
Les nombres des deux premiers types s'expriment aussi
sous la forme de fractions ou sous la forme de divisions de deux nombres. Ce
sont les nombres rationnels (on peut
faire des rations, des parts). Les nombres du troisième type ne peuvent pas se
transformer en fractions; ils sont irrationnels.
Le plus célèbre est la constante Pi,
mais il y en a bien d'autres. |
||
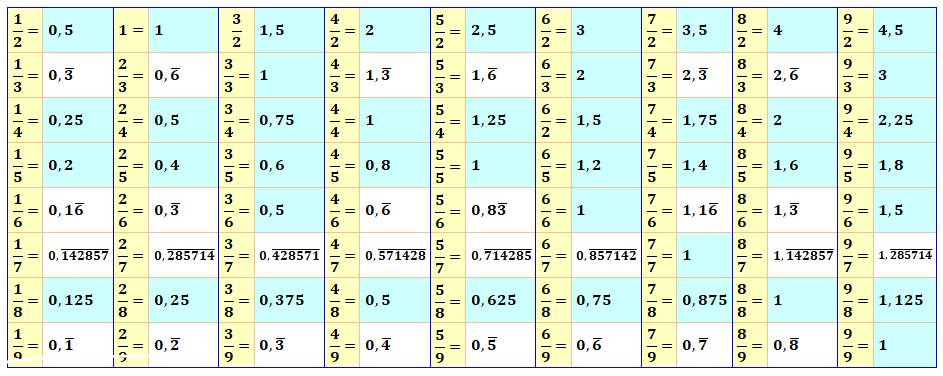
Toutes les fractions et leur développent
décimal jusqu'à 9/9
En bleu, les nombres décimaux; en
blanc, les nombres périodiques.
|
|
||
|
Fraction et son développement décimal |
Commentaires |
|
|
|
La
fraction la plus simple. Son
développement ne nécessite qu'une seule décimale significative (5). On
pourrait ajouter des 0 derrière le 5, mais ça ne changerait pas la valeur.
Donc, on ne fait pas. |
|
|
|
Le
nombre périodique le plus simple. La
période est 3, et elle n'a donc qu'un seul chiffre. |
|
|
|
Nombre
NON-périodique. Avec
½ et ¼ , les dénominateurs sont faits avec des 2. |
|
|
|
Nombre
NON-périodique. Le
dénominateur est 5, un diviseur de 10. |
|
Bilan
|
La fraction 1/1 n'est pas mentionnée; elle est banale;
elle vaut 1. Les trois fractions avec 2 ou 5 dans le dénominateur ne
sont pas périodiques. Nous verrons que c'est une règle générale.
|
|
|
Nombre
périodique de période 6. Notez
le chiffre 1 avant le 6. C'est
une partie fixe qui apparait avec de répéter le 6, sans fin. |
|
|
Premier
nombre périodique avec une période longue (6 chiffres). Notez
que: 6 = 7 – 1. Notez
aussi: 1 + 8 = 4 + 5 = 2 + 7 = 9. |
|
|
Nombre
NON-périodique. Encore
un dénominateur avec des 2 (8 = 2 x 2 x 2 = 23). |
|
|
Nombre
périodique avec répétition du 1. Notez
ce qui se passe lorsqu'on multiplie chaque côté par 9: Le
nombre 1 peut aussi s'écrire sous la forme de ces 9 répétés une infinité de fois. |
Bilan
|
Il existe des développements périodiques qui ne
commencent pas tout de suite après la virgule. C'est le cas de 1/6. Amusant: 2/7 = 0,285714
285714 …, les mêmes chiffres que pour 1/7, mais décalés de deux rangs. Même
chose pour les autres fractions en septièmes. |
|
|
Nombre
NON-périodique. Cette
égalité nous est familière comme l'est: 1/100 = 0, 01. Base
de l'écriture
décimale des nombres. Par
exemple: 0,45 veut dire 4 dixièmes plus 5 centièmes. |
|
|
Nombre
périodique avec période égale à 09 composée de deux chiffres. Sujet
d'amusement car 1 / 111 = 0,009009… et de même pour les autres nombres en 1. |
|
|
Nombre
périodique avec une partie fixe égale à 08, puis la période égale à 3. |
|
|
Nombre
périodique. Période
769323 de 6 chiffres. |
|
|
Nombre
périodique. Période
769323 de 6 chiffres avec partie fixe égale à 0. |
|
|
Nombre
périodique. Période
6. Partie
fixe 0. |
|
|
Nombre
NON-périodique. Dénominateur
= 16 = 2 x 2 x 2 x 2 = 24. Tous
les nombres avec dénominateur en puissance de 2 sont non-périodiques. |
Bilan
|
Un nombre périodique, comme 1/14, est donc caractérisé
par:
Amusant: prenez
les trois premières décimales (714) ajoutez-les aux trois dernières (285), on
obtient: 999. Cette somme en 9 arrive souvent avec les nombres périodiques. |
|
|
Nombre
périodique. Longueur
de la période 16 = 17 – 1. Celle-ci
ne peut jamais dépasser la valeur du dénominateur. |
|
|
Nombre
périodique. Période
5. Partie
fixe 0. |
|
|
Nombre
périodique. Longueur
de la période 18 = 19 – 1. Les
dénominateurs 19 comme 17 sont des nombres premiers. |
|
|
Nombre
NON-périodique. Tous
les dénominateurs qui sont le produit de 2 et de 5 forment des nombres
non-périodiques. |
Bilan
|
Avec un nombre premier p au dénominateur, il arrive
souvent que la longueur de la période soit maximale: égale à p – 1. Avec le
nombre premier 19, la période est égale à 18. Remarquez qu'avec le nombre premier 13, la longueur de
la période est égale à 6, la moitié de la longueur maximale (12). |
À suivre …
|
Toutes les remarques notées sur cette page annoncent
des propriétés générales que nous allons examiner dans les pages suivantes. |
![]()
|
|
|
|
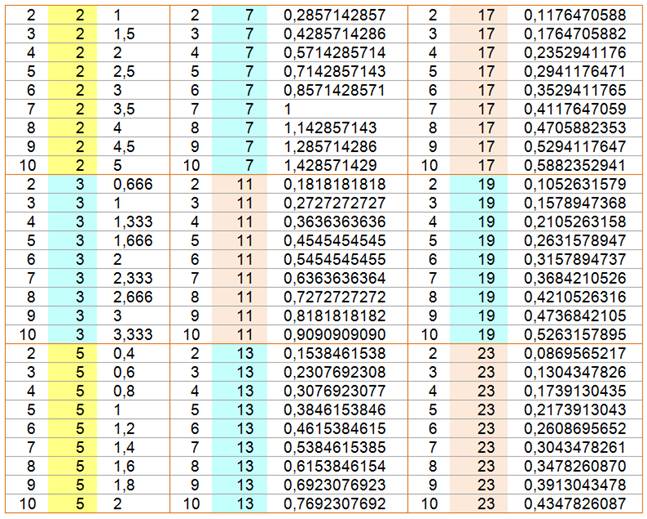
Table des divisions
des nombres de 2 à 10 par les nombres premiers de 2 à 23
|
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
Site |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Nombre/aaaCycli/NbCycDeb.htm |
![]()