|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
NOMBRES PÉRIODIQUES Configurations
remarquables Analyse des nombres périodiques particuliers. Observations. |
Développement décimal révélant les puissances des nombres

Voir Puissances dans la
période et autres configurations
|
|
||
|
Unité et répétition de nombres Puis extension |
|
|
|
Chiffres (presque) |
|
|
|
Puissance de 2 |
|
|
|
Puissance de 3 Puis généralisation |
|
|
|
Fibonacci |
|
|
|
Nombres entiers Puis extension |
|
|
|
Nombres impairs, suivis des nombres
pairs |
|
|
|
Nombres pairs, suivis des nombres
impairs |
|
|
|
Multiples de 5 Puis généralisation |
|
|
Comment trouver la fraction qui correspond à une suite de suite
de chiffres donnée
|
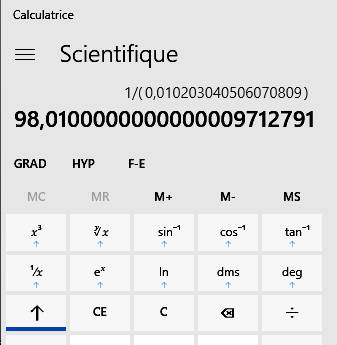
Procédure: 1.
Entrez le nombre
0,010203040506070809; 2.
Cliquez sur la flèche pour obtenir
le deuxième jeu de touches; 3.
Cliquez sur 1/x pour obtenir
l'inverse du nombre affiché; 4.
Vous obtenez le nombre 98,01000… La suite
des zéros indique que la fraction avec 9801 devrait convenir; et 5.
Vérifiez ce résultat en calculant la
fraction 100/9801. |
![]()
|
|
||
|
|
12, 12 12
12 12 … = 400 / 33 = 2 / 0,165 Nombre
cyclique. Celui-ci
est un exemple. Voyez
la liste à gauche. Notez
la répétition du multiple de 3. |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
Légende
|
|
|
Tableaux
|
|
Observations
|
![]()
Analyse
de cas particuliers
Le cas de 1/7 =
0,142758 … fait l'objet d'une page
complète
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Fraction en 1/49
0,040816326530612244897959183673469387755102
0408163265306122448979591836 0,061224489795918367346938775510204081632653
0612244897959183673469387755 0,081632653061224489795918367346938775510204
0816326530612244897959183673 0,102040816326530612244897959183673469387755
1020408163265306122448979592 0,122448979591836734693877551020408163265306
1224489795918367346938775510 Puissances de 2
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
DicoNombre |
|
|
Site |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Nombre/aaaCycli/NbCycCas.htm
|
![]()