|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
On dit primarité
(français) ou primalité (avec teinture anglo-saxonne)
![]()
|
NOMBRES de CARMICHAEL ou pseudo-premiers absolus (PPA) Parmi les exceptions au test de Fermat il y a les nombres pseudo-premiers. Les nombres de Carmichael sont de ce
type en plus fort ! Consultez la page Primalité pour une large introduction à ce sujet. |
|
|
|||||
|
Petit théorème de
Fermat – Version faible
Petit théorème de
Fermat – Version forte En divisant par a, avec précaution
|
Toutes les valeurs de a Si la version faible est vérifiée
pour toute valeur de a, on a un nombre pseudo-premier
absolu (PPA). Si la version forte est vérifiée pour
toute valeur de a, on a un nombre de Carmichael. On a démontré que tous les nombres
PPA sont aussi de Carmichael et réciproquement. Sierpinsky (page 233) |
||||
|
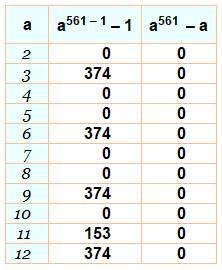
Approche par l'exemple Prenons le nombre composé 561 = 3 x 11 x 17. Avec la version faible du petit théorème (colonne de droite), pas de doute possible: ce nombre composé passe à travers le test quelle que soit la valeur de la base a, alors que 561 est un nombre composé. C'est un nombre PPA. Avec la version forte, le comportement
semble erratique. Il ne l'est plus si on élimine les valeurs de a multiples
des diviseurs de n (3, 11 et 17). C'est un nombre de Carmichael. Le nombre
561 est un nombre pseudo-premier absolu ou nombre
de Carmichael. Jusqu'à
100 000, ils sont 34 Jusqu'à 1 000 000, ils sont 108 Note: Les valeurs numériques sont tout de
suite faramineuses! En effet: a560 – 1 = 0,377… 10169 Le calcul utilise un algorithme de calcul modulaire qui réduit
considérablement les calculs et évite ces grands nombres. |
Exemple calcul avec p
= 561 et différentes bases a
|
||||
|
|
|||
|
Les
nombres de Carmichael sont des nombres composés qui satisfont le test de
Fermat pour toutes les bases a. |
|
||
|
|
||||
|
Infinité |
Ces nombres sont
rares, mais il en existe une infinité. Démontré en 1994
par Alfort, Grandville et Pomerance.
|
|||
|
Facteurs |
Tous impairs. Aucun facteur n'est
un carré. Il y a toujours
trois facteurs au moins: donc produit de trois nombres impairs premiers, au moins: |
|||
|
Théorème |
Par exemple 561 = 3 x 11 x 17 et 560 est divisible par
2, 10 et 16. |
|||
|
Ou nombres de
Chernick-Carmichael |
Jack Chernick a prouvé que tout nombre du
type: M = (6n + 1) × (12n + 1) × (18n + 1) est un nombre de Carmichael si les trois
facteurs sont premiers. 1729
est le nombre d'Hardy-Ramanujan (double somme de cubes). |
N,
m, p1, p2, p3 1, 1729, 7, 13, 19 6, 294409, 37, 73, 109 35, 56052361, 211, 421,
631 45, 118901521, 271, 541,
811 51, 172947529, 307, 613,
919 55, 216821881, 331, 661,
991 56, 228842209, 337, 673,
1009 100, 1299963601, 601,
1201, 1801 121, 2301745249, 727,
1453, 2179 195, 9624742921, 1171,
2341, 3511 206, 11346205609, 1237,
2473, 3709 216, 13079177569, 1297,
2593, 3889 255, 21515221081, 1531,
3061, 4591 276, 27278026129, 1657,
3313, 4969 370, 65700513721, 2221,
4441, 6661 380, 71171308081, 2281,
4561, 6841 426, 100264053529, 2557,
5113, 7669 … Suite en OEIS
A033502 |
||
|
et
historique |
|
|
En octobre 1640, dans une lettre à
Frenicle, Fermat écrit que p divise ap – a pour tout a, dès que p est premier. La question qui se pose: est-ce que seuls
les premiers satisfont ce critère? En 1899, Korselt avait mis en évidence un
critère de test pour caractériser de tels nombres: n
divise an – a pour tout
a si et seulement si n est un nombre sans carré et p – 1 divise n – 1 pour tout premier p
divisant n. En 1910, Carmichael montre que 561 = 3 x 11
x 17 divise a561 – a pour toute valeur de a. Carmichael
se plonge dans l'étude de ces nombres et développe un algorithme qui permet de construire
de tels nombre, nommés nombres de Carmichael. Il a l'intuition que ces
nombres sont en quantité infinie. En 1939, Chernick trouve une manière de les
construire: Si p = 6m, q = 12m +1 et r = 18m + 1 sont
tous trois premiers, alors N = p.q.r et un nombre de Carmichael. Alors, on peut en créer une infinité? En 1992, W.R. Alford, Andrew Granville et
Carl Pomerance démontrent que les nombres de Carmichael sont en quantité
infinie en prouvant que: Pour x suffisamment grand, il existe plus
de x2/7 nombres de
Carmichael. |
|
![]()
|
|
||
|
561 2 465 2 821 6 601 8 911 10 585 … |
3 x 11 x 17 5 x 13 x 17 7 x 13 x 19 5 x 17 x 29 7 x 13 x 31 7 x 23 x 41 7 x 19 x 67 5 x 29 x 73 |
|
|
|
|
|
Quantité de Carmichael infinité: OUI Quantité de Carmichael à k facteurs existent
toujours: ? Quantité de Carmichael à 3 facteurs infinité: ? Quantité de Carmichael à 3 facteurs < 1012 = 1 000 Quantité de Carmichael à k facteurs < 1012
= 8 241 |
|
|
NOMBRE DE CARMICHAEL le
plus petit pour une quantité croissante de facteurs |
|
|||
|
Qté |
n |
|
Facteurs |
|
|
2 |
|
|
||
|
3 |
561 |
= |
3 x 11 x 17 |
|
|
4 |
41 041 |
= |
7 x 11 x 13 x 41 |
|
|
5 |
825 265 |
= |
5 x 7 x 17 x 19 x 73 |
|
|
6 |
321 197 185 |
= |
5 x 19 x 23 x 29 x 37 x 137 |
|
|
7 |
5 394 826 801 |
= |
7 x 13 x 17 x 23 x 31 x 67 x 73 |
|
|
8 |
232 250 619 601 |
= |
7 x 11 x 13 x 17 x 31 x 37 x 73 x
163 |
|
|
9 |
9 746 347 772 161 |
= |
7 x 11 x 13 x 17 x 19 x 31 x 37 x 41
x 641 |
|
|
10 |
1 436 697 831 295
441 |
= |
11 x 13 x 19 x 29 x 31 x 37 x 41 x
43 x 71 x 127 |
|
|
Liste |
561,
41041, 825265, 321197185, 5394826801, 232250619601, 9746347772161,
1436697831295441, 60977817398996785, 7156857700403137441,
1791562810662585767521, 87674969936234821377601, 6553130926752006031481761,
1590231231043178376951698401 |
|||
|
à 3
facteurs premiers |
|
|||
|
Carmichael |
|
Facteurs premiers |
PPCM* |
|
|
= |
3 x 11 x 17 |
80 |
||
|
= |
5 x 13 x 17 |
48 |
||
|
= |
7 x 13 x 19 |
36 |
||
|
2 465 |
= |
5 x 17 x 29 |
112 |
|
|
2 821 |
= |
7 x 13 x 31 |
60 |
|
|
6 601 |
= |
7 x 23 x 41 |
1 320 |
|
|
8 911 |
= |
7 x 19 x 67 |
198 |
|
|
10 585 |
= |
5 x 29 x 73 |
504 |
|
|
15 841 |
= |
7 x 31 x 73 |
360 |
|
|
29 341 |
= |
13 x 37 x 61 |
180 |
|
|
46 657 |
= |
13 x 37 x 97 |
288 |
|
|
52 633 |
= |
7 x 73 x 103 |
1 224 |
|
|
115 921 |
= |
13 x 37 x 241 |
720 |
|
|
162 401 |
= |
17 x 41 x 233 |
2 320 |
|
|
252 601 |
= |
41 x 61 x 101 |
|
|
|
294 409 |
= |
37 x 73 x 109 |
216 |
|
|
314 821 |
= |
13 x 61 x 397 |
1 980 |
|
|
334 153 |
= |
19 x 43 x 409 |
8 568 |
|
|
399 001 |
= |
31 x 61 x 211 |
840 |
|
|
488 881 |
= |
37 x 73 x 181 |
360 |
|
|
512 461 |
= |
31 x 61 x 271 |
540 |
|
|
530 881 |
= |
13 x 97 x 421 |
3 360 |
|
|
1 152 271 |
= |
43 x 127 x 211 |
630 |
|
|
1 193 221 |
= |
31 x 61 x 631 |
1 260 |
|
|
1 461 241 |
= |
37 x 73 x 541 |
1 080 |
|
|
4 335 241 |
= |
53 x 157 x 521 |
1 560 |
|
|
5 968 873 |
= |
43 x 127 x 1 093 |
3 276 |
|
|
14 913 991 |
= |
43 x 127 x 2 731 |
8 190 |
|
|
15 247 621 |
= |
61 x 181 x 1 381 |
4 140 |
|
|
17 098 369 |
= |
113 x 337 x 449 |
1 344 |
|
|
17 316 001 |
= |
53 x 157 x 2 081 |
6 240 |
|
|
23 382 529 |
= |
97 x 193 x 1 249 |
2 496 |
|
|
60 957 361 |
= |
61 x 181 x 5 521 |
16 560 |
|
|
362 569 201 |
= |
113 x 337 x 9 521 |
28 560 |
|
En jaune, la plus petite
valeur pour ce nombre de facteurs
PPCM* au sens des gaussiens
|
à 4
facteurs premiers |
|
|||
|
Carmichael |
|
Facteurs premiers |
PPCM* |
|
|
41 041 |
= |
7 x 11 x 13 x 41 |
120 |
|
|
62 745 |
= |
3 x 5 x 47 x 89 |
2 024 |
|
|
63 973 |
= |
7 x 13 x 19 x 37 |
36 |
|
|
75 361 |
= |
11 x 13 x 17 x 31 |
||
|
101 101 |
= |
7 x 11 x 13 x 101 |
||
|
126 217 |
= |
7 x 13 x 19 x 73 |
72 |
|
|
172 081 |
= |
7 x 13 x 31 x 61 |
6O |
|
|
188 461 |
= |
7 x 13 x 19 x 109 |
108 |
|
|
278 545 |
= |
5 x 17 x 29 x 113 |
||
|
340 561 |
= |
13 x 17 x 23 x 67 |
||
|
449 065 |
= |
5 x 19 x 29 x 163 |
||
|
552 721 |
= |
13 x 17 x 41 x 61 |
||
|
656 601 |
= |
3 x 11 x 101 x 197 |
||
|
658 801 |
= |
11 x 13 x 17 x 271 |
||
|
670 033 |
= |
7 x 13 x 37 x 199 |
396 |
|
|
748 657 |
= |
7 x 13 x 19 x 433 |
432 |
|
|
838 201 |
= |
7 x 13 x 61 x 151 |
300 |
|
|
852 841 |
= |
11 x 31 x 41 x 61 |
120 |
|
|
997 633 |
= |
7 x 13 x 19 x 577 |
576 |
|
|
1 033 669 |
= |
7 x 13 x 37 x 307 |
612 |
|
|
1 082 809 |
= |
7 x 13 x 73 x 163 |
648 |
|
|
1 569 457 |
= |
17 x 19 x 43 x 113 |
||
|
1 773 289 |
= |
7 x 19 x 69 x 199 |
||
|
2 100 901 |
= |
11 x 31 x 61 x 101 |
300 |
|
|
2 113 921 |
= |
19 x 31 x 37 x 97 |
||
|
2 433 601 |
= |
17 x 37 x 53 x 73 |
||
|
2 455 921 |
= |
13 x 19 x 61 x 163 |
||
|
2 531 845 |
= |
5 x 19 x 29 x 919 |
||
|
2 628 073 |
= |
7 x 37 x 73 x 139 |
||
|
… Quelques
autres ci-dessous. Voir sites pour plus |
||||
|
4 909 177 |
= |
7 x 13 x 73 x 739 |
2 952 |
|
|
8 341 201 |
= |
11 x 31 x 61 x 401 |
1 200 |
|
|
10 837 321 |
= |
11 x 31 x 61 x 521 |
1 560 |
|
|
16 046 641 |
= |
13 x 37 x 73 x 457 |
1 368 |
|
|
27 062 101 |
= |
11 x 31 x 61 x 1301 |
3 900 |
|
|
33 302 401 |
= |
11 x 31 x 61 x 1601 |
4 800 |
|
|
37 354 465 |
= |
5 x 29 x 73 x 3 529 |
3 528 |
|
|
43 286 881 |
= |
11 x 31 x 61 x 2 081 |
6 240 |
|
|
à 5
facteurs premiers |
|
|||
|
Carmichael |
|
Facteurs premiers |
PPCM* |
|
|
825 265 |
= |
5 x 7 x 17 x 19 x
73 |
144 |
|
|
101 957 401 |
= |
7 x 13 x 19 x 109 x
541 |
540 |
|
|
1 150 270 849 |
= |
7 x 13 x 19 x 577 x
1 153 |
1 152 |
|
|
7 103 660 473 |
= |
7 x 13 x 19 x 109 x
37 693 |
37 692 |
|
|
à 6
facteurs premiers |
|
|||
|
Carmichael |
|
Facteurs premiers |
PPCM* |
|
|
321 197
185 |
= |
5 x 19 x 23 x 29 x 37 x 137 |
94 248 |
|
|
1 039 531
253 629 141 |
= |
7 x 13 x 19 x 109 x 541 x 10 195 741 |
10 195 740 |
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Référence |
|
|
|
|
|
Cette page |
![]()