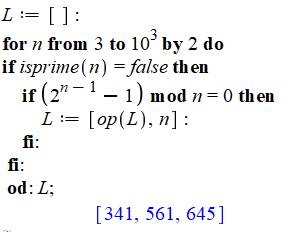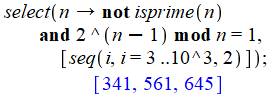NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 13/12/2019 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	Nombres PREMIERS
Débutants Nombres Premiers	Recherche de PRIMALITÉ					Glossaire Nombres Premiers
INDEX Nombres premiers	Crible d'Ératosthène		Presque-premiers	Pseudo Premiers	Carmichael
	Divisibilité			Nombres de Poulet	Carmichael - Texte
	Primalité			Liste pseudo-P.
		Sommaire de cette page >>> Nombres de Poulet >>> Démonstrations >>> Propriétés >>> Nombre pseudo-premier pair à base 2 >>> Liste des nombres de PPF-2 (Poulet numbers) >>> Liste des nombres de Poulet (Super-poulet numbers)

On dit primarité (français) ou primalité (avec teinture anglo-saxonne)

Nombres pseudo-premiers de Fermat base 2

Nombres de POULET

Ou Nombres de SARRUS ou Fermatians

Parmi les exceptions au test de Fermat, il y a les nombres pseudo-premiers. Et parmi eux les nombres de Poulet mettant en jeu des puissances de 2.

Anglais: Fermat pseudoprimes to base 2, also called Sarrus numbers or Poulet numbers

Nombres de Poulet – Trois races !
2-FPP Les nombres composés qui satisfont la version forte sont appelés pseudo-premiers de Fermat base 2 2-FPP ou simplement 2-PP. Voir Fermat fort et faible	Exemple Voir Rappel sur la notation modulo
POULET Les pseudo-premiers impairs en base 2 pour la version faible sont appelés: nombres de Poulet. Poulet = 2-FPP Comme n > 2 est premier avec 2 (n est impair), on peut diviser par 2 et retrouver la version forte: les nombres de Poulet sont également 2-PP	Exemple Définition Wolfram MathWorld
2-FPPpair Si n est pair, on parlera de pseudo-premiers pairs de Fermat à base 2. Ces nombres découverts plus récemment font l'objet d'un traitement particulier. Ils passent la condition faible, mais pas la condition forte. Certains nomment fermatians les nombres 2-FPP pairs comme impairs.	Exemple avec n pair (non nombre de Poulet) Notez qu'en version forte
SUPER-POULET Les nombres super-Poulet sont les nombres dont tous les diviseurs satisfont la relation de Fermat faible. Les Anglo-saxons nomment ces nombres: super-Poulet Numbers	Exemple 371 = 11 x 31

Voir Nomenclature des nombres pseudo-premiers de Fermat

Démonstrations
Pourquoi 341 est Poulet ? 11 et 31 sont premiers impairs Prouvez que: Note La barre verticale veut dire: divise Voir Nombre 341	On calcule facilement Valables pour les multiples de 10 Traduction en termes de divisibilité Le produit divise aussi l'expression
Prouvez que 336 408 382 est Poulet 336 408 382 = 2 · 73 · 1103 · 2089 Sachant que m = 2 · 73 · 1103 = 161 038 est Poulet	n = 2089 m n – 1 = (m – 1) 2089 + 2088 Or: 2088 = 2^3 · 9 · 29 Et avec: 9 | (m – 1) et 29 | (m – 1) On déduit: 9 | (n – 1) et 29 | (n – 1) Or: 2^9 – 1 = 7 · 73 Et: 2^29 – 1 = 233 · 1103 · 2089 73 | 2^9 – 1 => 73 | (2^n – 1 – 1) 1103 | 2^29 – 1 => 1103 | (2^n – 1 – 1) Comme: 2089 | 2^29 – 1 => 2089 | 2^n – 1 – 1 Compte tenu de la factorisation de n => n | (2^n– 2)
Pourquoi 2047 est super-Poulet ? Voir Nombre 2 047	Fermat Ce qui prouve que 2047 est PP (Poulet) Pour les diviseurs (Fermat): 23 | 2^23 – 2 89 | 2^89 – 2 Ce qui prouve que 2047 est super-Poulet.
Aucun super-Poulet (SP) n'est pair	Si 2n est super-Poulet 2n | (2^2n– 2) => n | (2^2n– 1) => n est impair Or 2n est SP => n | (2^n– 2) Avec n impair n | (2^n – 1– 1) n | (2^2n – 1– 2^n – 1 ) = 2^n – 1 (2^n – 1) Avec n impair n | (2^n – 1) Avec n | (2^n– 2) => n = 1 Impossible n car est composé.

Démonstrations selon référence Sierpinsky

Propriétés
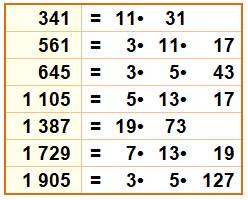
Historique des nombres de Poulet (2PP) P. Poulet a établi la liste de ces nombres jusqu'à 10^8. C.Pomerance, J.L. Selfridge et S.S.Wagstaff Jr. Sont allé jusqu'à 25 10^9.	Les plus petits avec leurs facteurs
Un nombre de Poulet, produit de deux facteurs premiers distincts, est un super-Poulet	Il existe une infinité de paire (p et q) telle que: pq | 2^pq – 2 Donc, une infinité de super-Poulet. Il est aussi prouvé qu'il existe une infinité de super-Poulet sans être Poulet.
Si n est un 2PP impair, alors le nombre m = 2^n – 1 est aussi un PP impair Il y en a donc une infinité. Il y a une infinité de Mersenne 2PP. On ne sait pas dire pour les super-Poulet.	Il en existe aussi une infinité de la forme ax + b (a et b étrangers)
P(x) = quantité de PP < x C. Pomerance estime pour x grand:

Nombre pseudo-premier pair à base 2 (2PPpair) (even base-2 pseudoprimes)
D.H. Lehmer découvre en 1950 un pseudo-premier pair de Fermat à base 2 en version faible (2FPP pair) n = 161 038 Qui, lorsqu'il est connu, est facile à prouver (démo de Sierpinski) Les 2FPPpairs les plus petits 161 038 215 326 209 665 666 4 783 964 626 1 656 670 046 626 1 202 870 727 916 606 N.G. Beeger a montré il y en a une infinité de 2PPpair.	Pourquoi 161 038 est 2PPpair ? On vérifie assez facilement que: n = 161 038 = 2 · 73 · 1103 n – 1 = 3² · 29 · 617 2^9 – 1 = 7 · 73 2^29 – 1 = 233 · 1103 · 2089 Or 9 | (n – 1) ⇨ 2^9 | 2^(n – 1) ⇨ (2^9 – 1) | (2^n – 1 – 1) 29 | (n – 1) ⇨ 2^29 | 2^(n – 1) ⇨ (2^29 – 1) | (2^n – 1 – 1) Avec 73 | 2^9 – 1 et 1103 | 2^29 – 1 On déduit par transistivité (exemple en rose): 2^n – 1 – 1 divisible par 73 et par 1103 2^n – 2 divisible par 73 et 1103 C'est un nombre pair: facteur 2. En se référant à la factorisation complète de n: n | 2^n – 2 et n est un PP

Liste des nombres de 2-PPF – Nombres de Poulet
Ou	341, 561, 645, 1105, 1387, 1729, 1905, 2047, 2465, 2701, 2821, 3277, 4033, 4369, 4371, 4681, 5461, 6601, 7957, 8321, 8481, 8911, 10261, 10585, 11305, 12801, 13741, 13747, 13981, 14491, 15709, 15841, 16705, 18705, 18721, 19951, 23001, 23377, 25761, 29341, 30121, 30889, 31417, 31609, 31621, 33153, 34945, 35333, 39865, 41041, 41665, 42799, 46657, 49141, 49981, 52633, 55245, 57421, 60701, 60787, 62745, 63973, 65077, 65281, 68101, 72885, 74665, 75361, 80581, 83333, 83665, 85489, 87249, 88357, 88561, 90751, 91001, 93961 … Les nombres en rouge sont des nombres super-Poulet.
Programme classique Forme compacte		Programme Maple Déclaration d'une liste nommé L. Boucle examinant les nombres n de 3 à 1000 par pas de 2; nombres composés impairs seulement. On ne retient que les n non premiers et ceux dont 2^t – 1 donne un reste de 1 lorsque divisé par n. Forme compacte établie d'après idée de Robert Israel. Elle exige une certaine aisance avec le language.

Voir Programmation – Index

Liste des nombres super-Poulet
Pour tout D diviseur de n	341, 1387, 2047, 2701, 3277, 4033, 4369, 4681, 5461, 7957, 8321, 10261, 13747, 14491, 15709, 18721, 19951, 23377, 31417, 31609, 31621, 35333, 42799, 49141, 49981, 60701, 60787, 65077, 65281, 80581, 83333, 85489, 88357, 90751, … Les nombres en rouge ne sont pas 2FPP
Programme classique Forme compacte		Programme Maple Déclaration d'une liste nommé L. Appel au package de théorie des nombres. Boucle examinant les nombres n de 3 à 2500 par pas de 2. On ne retient que les n non premiers et ceux dont tous (andmap) les diviseurs premiers (factorset) sont tels que 2 à leur puissance donne 2 comme reste en les divisant par n. Forme compacte établie d'après idée de Robert Israel. Elle utilise une procédure (poulet). Select ne retient que les valeurs de i pour poulet vrai. Numtheory n'est déclaré que localement. Ouverture de factorset, sans ouvrir tout le package.

Merci à Stephan CEROI pour les précisons importantes apportées à cette page

Suite	Nombres de Carmichael Nombres premiers – Index
Voir	Modulo & Congruences Nombres Premiers Petit théorème de Fermat Presque premiers Pseudo Premiers Absolus Théorie des nombres
Sites	Poulet Number – Wolfram MathWorld A001567 – Fermat pseudoprimes to base 2, also called Sarrus numbers or Poulet numbers A050217 - Super-Poulet numbers: Poulet numbers whose divisors d all satisfy d|2^d-2 A270973 - Smallest base-2 even pseudoprime Autres références
Cette page	http://villemin.gerard.free.fr/ThNbDemo/Poulet.htm