|
|||||||||||||||||||||||||||||||||||||
On dit primarité
(français) ou primalité (avec teinture anglo-saxonne)
![]()
|
Ce nombre est-il PREMIER? Comment
s'y prendre pour savoir si un nombre est premier? Un
premier test consiste à appliquer les critères
de divisibilité courants: par 2, 3, 5, 9, 11 … Et si
le nombre résiste, comment aller plus loin ? Quels
sont les outils à notre disposition? Les cribles sont des algorithmes qui détectent tous les
nombres premiers jusqu'à une limite n. Le nombre d'opérations pour tester si un nombre est premier
croit exponentiellement avec le nombre de chiffres. Il faut beaucoup, beaucoup
plus d'opérations pour tester un nombre de 51 chiffres par rapport à un
nombre à 50, par exemple. À partir d'une certaine taille de nombres, il
faudrait des journées, des années, des milliards d'années … de calculs par
ordinateur. La sécurité des communications (cryptage)
est basée sur la difficulté à factoriser de grands nombres. |
Voir Programmes de recherche
classique des nombres premiers
|
|
|||||||||||||||||||||||||||||||||||
|
27 489 ?
2
+ 7 + 4 + 8 + 9 =
9 + 12 + 9 =>12
=>
3 Ce
nombre est divisible par 3
|
427 741 ?
|
||||||||||||||||||||||||||||||||||
|
27
489 = 3 x 7 x 7 x 11 x 17 Il existe des cas où il est facile de trouver si un
nombre est premier. |
427
741 = 521 x 821 Plus le nombre est grand, surtout s'il a de grands
facteurs, et plus il est difficile de
trouver les facteurs premiers. |
||||||||||||||||||||||||||||||||||
|
|
Voir Nombres à
facteurs proches de la racine carrée
Voir site: Poème sur le nombre 2021 et la recherche de ses facteurs
|
|
||
|
La
méthode la plus simple pour tester si un nombre est premier consiste à
effectuer la division
par les nombres successifs et à constater qu'aucun reste n'est nul. En fait,
il est suffisant* d'aller jusqu'à la racine
carrée de n. Prenons le nombre 100 qui est divisible par 2, 4,
5, 10, 20, 25 et 50. On peut donc limiter à n/2. Mais, constatons qu'il y a
encore de la redondance puisque, par exemple 2 x 50 = 100. Dire que 100 est
divisible par 2 induit qu'il divisible par 50. Idem pour 4 x 25; 5 x 20 et
10x 10. Ce dernier est la plus grand et, c'est le produit des racines carrées
de 100. On élimine facilement les nombre divisibles par
2, 3 et 3 en utilisant les critères simples de divisibilité. À ce
stade, on se retrouve avec une liste de nombre qui commence par: Continuer
à tester la divisibilité par les nombres premiers suivants (7, 11, 13…) est
la méthode la plus connue et cela depuis l'Antiquité. C'est le crible
d'Ératosthène. On
améliore la méthode de recherche en constatant que les nombres
premiers sont proches à 1 près des multiples de 6. Ils sont de la forme 6k – 1 o u 6 k + 1.
Ceci du fait que (6k, 6k + 2 et 6k + 4) sont divisibles par 2; 6k + 3 par 3.
Restent 6k + 1 et 6k + 5 équivalent à 6k' – 1. La
vitesse est multipliée par 3. |
Il est
possible de généraliser la méthode du 6k. On note
n# la primorielle de n, qui est le produit des nombres premiers
inférieurs à n ou égal à n. Tous les
nombres plus grands que n# sont évidemment de la forme n#. k + i pour i
prenant toutes les valeurs inférieures à n#. Certaines valeurs de i
conduisent à des nombres composés facilement reconnaissables. Avec 6#, par exemple, on a 6# = 2 x 3 x 5 = 30.
Or, tout nombre est de la forme 30k + i avec i = {0, 1, 2, 3…, 29}. Tous ceux
avec i divisible par 2, 3 ou 5 sont composés. Pour qu'un nombre soit premier, il ne reste que i
= {1, 7, 11, 13, 17, 19, 23, 29}. Ce sont d'ailleurs les nombres i tels que
PGCD (1, 30) = 1 (autrement dit: i est premier avec 30). Bilan: tous les
nombres premiers sont de la forme 30k + i
avec i = {1, 7, 11, 13, 17, 19, 23, 29}. Mais tous les nombres de
cette forme ne sont pas premiers. Exemple de nombre composé: 437 = 19 x 23 = 7# k +
i = 2 x 210 + 17. Or plus n augmente, plus les nombres premiers se
raréfient et moins il y a de possibilités pour i. Le test de primalité
deviendrait plus efficace. Néanmoins, il faut toujours tester tous les
premiers inférieurs à n et cela revient pratiquement au crible d'Ératosthène. Le moyen
souvent utilisé avant de s'en remettre à des méthodes plus sophistiquées,
consiste à constituer la table
des 100 ou 200 plus petits nombres premiers et à tester la divisibilité par
ces valeurs du nombre considéré. |
|
*Racine carrée, c'est suffisant !
|
Un
argument plus rapide est le suivant: Un
entier composé a un facteur premier inférieur ou égal à sa racine carrée. En
effet: tout entier composé peut-être décomposé en une multiplication de deux
nombres; ce qui correspond à l'aire d'un rectangle ou celle d'un carré. La
largeur est au plus égale à la longueur. La largeur est donc un nombre
inférieur ou égal à la racine carrée. La
largeur étant soit un nombre premier, soit un multiple de nombre premier. Ex:
35 = 5 x 7 et 5 < 5,9… la racine carrée de 35. |
|
des
NOMBRES PREMIERS |
|
|
|
Un premier outil bien
utile. Pour s'en faire une petite idée …
Plus clairement: quand p est
premier, si on divise (a à la
puissance p-1) par p le reste
est 1. La
valeur de a importe
peu pourvu que ce ne soit pas un multiple de p, car dans
ce cas cette puissance serait divisible par p et le
reste serait 0. Exemples: p = 5 et a
= 3 => 3^(5-1) = 81 et 81 = 5 x 16 + 1. p = 5 et a = 10 => 10^(5-1)
= 1000 et 1000 = 5 x 200 + 0.
Pour un nombre à 100 chiffres, la
méthode du crible nécessite 1050 opérations; tandis que cette méthode ne
nécessite seulement que 300 opérations.
Exemple avec 341 = 11 x 31, en
prenant a
successivement égal à 2 et 3 2341 – 1
=
341k + 1 Le reste de la division par 341
est 1. Le
test de Fermat laisse passer ce nombre composé avec a = 2. Le
nombre 341 est dit pseudo-premier. 3341 – 1 =
341k + 56 Le reste de la division par 341
est 56. Avec
a = 3, le test de Fermat confirme que ce nombres est composé. Nous
verrons qu'il existe des nombres rebelles qui passent le test même avec
différentes valeurs de a. Ce sont les nombres pseudo-premiers
absolus. Le
nombre 341 étant le plus petit résistant au test de Fermat, tous les nombres
jusqu'à 342, seront bien détectés comme premier.
|
||
|
|
||
|
On peut chercher en divisant par les
nombres inférieurs. On y passerait son existence !
Le théorème de Lucas -
Lehmer
Le test de Lucas -
Lehmer
Il est aussi possible de démarrer avec S(1)
= 10 ou d'autres valeurs selon p. En pseudo code ce test
devient: Lucas_Lehmer_Test(p): s := 4; pour i de 3 à p faire
s := s2 – 2 mod 2p – 1; si s == 0 alors 2p – 1n
est premier sinon 2p
– 1 est composé; |
||
Voir Exemple de calcul
|
|
||
|
Trois
mathématiciens indiens trouvent un nouvel algorithme pour tester la primalité
d'un entier qui indique si n est premier
ou n est composé en un temps qui est un polynôme de la
taille de n. C'est le premier du genre |
||
|
Trois chercheurs
indiens mettent au point un algorithme
de test pour les très grands nombres. Pour un même temps
de calcul par ordinateur, il permet de tester des nombres beaucoup plus grands
en utilisant que les méthodes connues jusqu'alors. L'algorithme est
pourtant relativement simple. Il est
performant. Il s'agit d'une habile combinaison de tests déjà connus. La recherche des
nombres premiers est un problème polynomial, affirment ces jeunes chercheurs
(primes is in P) Voir Voyageur de
commerce |
PRIMES is
in P Manindra Agrawal, Neeraj Kayal and Nitin Saxena Department of Computer Science & Engineering Indian Institute of Technology Kanpur Kanpur-208016, INDIA August 6, 2002 Abstract We present a deterministic polynomial-time algorithm
that determines whether an input number n is prime or
composite. Voir Suite sur leur site |
|
Voir Août 2002
![]()
|
|
||
|
Le petit
théorème de Fermat énonce: |
Si p est premier impair
alors: 2p – 1 – 1 est divisible
par p |
|
|
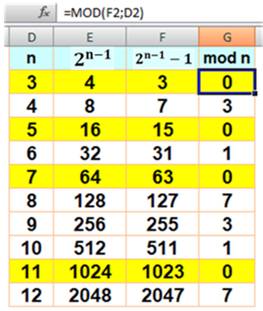
Implémentation sur tableur Il est
possible de pratiquer une recherche simple des nombres premiers sur le tableur. Il s'agit
d'un exercice d'entrainement sur cet outil et un exercice de découverte du
petit théorème de Fermat. La recherche est, en effet, limitée aux petits
nombres (jusqu'à 30) du fait que la puissance de 2 qui grimpe rapidement. Colonne 1: les nombres de 3 à n; Colonne 2: le nombre 2 à la puissance n; Colonne 3: idem moins 1; et Colonne 4: calcul du reste de la division de ce
nombre (en colonne 3) par n via la fonction mod
(résultat semblable en faisant simplement la division et en constant qu'elle
tombe juste ou pas) En jaune: reste nul et identification des nombres
premiers: 3, 5, 7, 11 … |
|
|
|
Implémentation avec logiciel
(Maple) Aussi
rapide qu'avec le tableur à la différence que ces logiciels savent manipuler de
très grands nombres. Boucle d'exploration des nombres de 3 à 20 (par
exemple); Calcul de N selon la formule de Fermat; Recherche conditionnelle: si ce nombre N est
divisible par n (via calcul mod), alors imprimer le nombre n. On en profite
pour indiquer la valeur du grand nombre N et son quotient par n. Le logiciel
authentifie la primalité de n (isprime) |
|
|
|
Les
spécialistes savent que si p est premier le test est bon; mais,
réciproquement, si le test est bon, le nombre n'est pas forcément premier. Le premier cas se présente pour 341
Ces nombres comme 341 sont appelés pseudo-premiers. Remède Introduire un deuxième test (les puissances de 3
par exemple). Ci-contre, le programme élimine bien 341, cette fois. Hélas, il existe de rares nombres qui résistent
encore, les pseudo-premiers
absolus. |
|
|
Voir Programmation – Index
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Calcul en
ligne |
|
|
Cette page |
![]()