|
||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
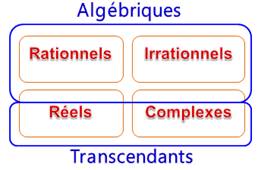
NOMBRES ALGÉBRIQUES Algébriques
= tous les nombres, racines d'une
ÉQUATION non nulle à coefficients rationnels. Les autres, non-algébriques, sont
appelés Transcendants.
Tous les nombres rationnels
et irrationnels sont algébriques. Les nombres réels et
complexes sont algébriques sauf les nombres transcendants. |
Anglais: Algebraic numbers
Voir Algébrique dans le DicoMot Maths /
Place des algébriques parmi les nombres
|
|
|
|
Un
nombre algébrique est un nombre
réel ou complexe, solution d'une équation
polynomiale non-nulle à coefficients rationnels. Autrement-dit:
il peut être défini par une expression plus ou moins compliquée. Par
exemple, racine de deux est
solution de l'équation x² – 2 = 0. Ce
nombre est algébrique. Il est aussi irrationnel.
C'est un nombre algébrique irrationnel.
Voir Diagramme L'expression
générale est un polynôme de la forme:
Les
nombres algébriques sont un sous-ensemble des nombres réels, excluant les
nombres transcendants. Algebraic Numbers: any number that is a solution to a polynomial equation with rational
coefficients. Include all Rational Numbers, and some
Irrational Numbers. |
|
|
|
|
|
|
|
|
|
||
|
Entier algébrique: nombre réel ou complexe,
solution (ou racine) d'une équation polynomiale de degré quelconque, dont
tous les coefficients sont des nombres entiers, et dont le coefficient du
terme de plus haut degré vaut 1. |
Solution de: x² – 2 = 0 est un entier algébrique.
Solution de: 2x²
– 3 = 0 n'est pas un entier algébrique.
Solution de: x² +1 = 0 est un entier algébrique. |
|
![]()
|
Suite |
|
|
Voir |
|
|
Nombres |
|
|
Site |
|
|
Cette page |
![]()