NOMBRES - Curiosités, théorie et usages

Accueil / Dictionnaire / Rubriques / Index / Atlas / Références /    Nouveautés

ORIENTATION GÉNÉRALE    -   M'écrire   -   Édition du: 23/01/2013

Débutants

Général

TYPES  NOMBRES / TYPES

Glossaire

Nombres

 

NOMBRES

 DÉBUTANTS

 

 

Sommaire de cette page

>>> APPROCHE

>>> HISTORIQUE

>>> PROPRIÉTÉS

>>> QUELQUES NOMBRES TRANSCENDANTS

>>> EXEMPLES PARTICULIERS

 

Retour vers Index de ces pages

 

 

 

Les divers types de NOMBRES

 

 

*    Les nombres, c'est facile!

*    Page dédiée aux débutants, novices, juniors …

Voir Orientation sur les types de nombres

 

 

 APPROCHE

 

DEUX races principales dans le monde des nombres – Nombres réels

 

*    On connaît les nombres pour compter dans la vie de tous les jours:

2  3  4  5 …

 

*    Il y a aussi ceux qui ont une virgule et des chiffres derrière:

1,25    3,14   0,222  …

 

 

 

 

TROIS types de nombres à virgule – Nombres décimaux

 

*    Il a des nombres à virgule qui sont simples et gentils.
La quantité de chiffres derrière la virgule est fixe.
Ils correspondent à une découpe en parts (rations) simples, à une fraction simple.

0,5 = 1/2

0,25 = 1/4

 

*    Il a ceux plus facétieux qui jouent à ne jamais s'arrêter de répéter leurs chiffres.
Ils correspondent à des fractions plus compliquées.

1 / 3 = 0, 3 3 3 3 3 3 ….

1 / 7 = 0,142857 142857 14 …

 

*    Il y a ceux qui ont un grain de folie.
Les chiffres après la virgule semblent provenir du pur hasard.

1,414 213 562 373 095 …  = 2

 

 

 

 

DEUX sortes de nombres un peu fous – nombres irrationnels

 

 

*    Il y a les compréhensifs qui se laissent faire.
Une formule simple (équation) les décrit.

x² = 2

Qui donne:

x = 2= 1,414 213 562 373 095 … 

Note: nous avons vu que ce nombre est décimal, car il a des chiffres après la virgule.

 

 

*    Les pires sont ceux refusent de se laisser discipliner.
Aucune équation à coefficients entiers ne peut les définir.
Ce sont les transcendants.

3,141 592 653 589 793 …  =

 

Note:

*    On peut trouver des transcendants avec une répartition régulière de leurs chiffres. C'est le cas du premier transcendant inventé par Liouville:

0,10 100 1000 10000 100000 ....

 

 

Vite un diagramme pour m'y retrouver …

 

 

 

PREMIER BILAN

 

Selon leurs décimales

 

2

= 2, 000 …

*      ENTIER

1/2

= 0, 500 …

*      Fractionnaire ou RATIONNEL

Entiers et rationnels sont des décimaux: Ils n'ont pas de chiffres derrière la virgule ou alors un nombre limité.

1/3

= 0, 333333…

*      Fractionnaire périodique répétitif e période 1

1/7

= 0, 142857
       142857 …

*      Fractionnaire périodique de période 6

= 1, 414 213

       562 373 095 …

*      Non fractionnaire ou IRRATIONNEL

Il existe une égalité pour le définir: x² = 2

= 3, 141 592

       653 589 793 …

*      Non fractionnaire, donc irrationnel,

mais il n'existe pas d'égalité simple pour le définir, il est TRANSCENDANT

 

Il existe une infinité de nombres.

Ils sont aussi très variés.

 

*      Naturel

Natural numbers

1, 2, 3 …

*      Entier positif

Whole numbers

Naturel avec le 0

*      Relatif ou entier

Integer

Entiers et négatifs

*      Rationnel

Rational

Fractions

*      Irrationnel

Irrational

Comme  ou le nombre d’or

*      Transcendant

Transcendental

Comme pi et e, racine d’aucun polynôme

*      Réel

Real

Tous ceux cités ci-dessus

*      Imaginaire

Imaginary

Réel multiplié par

*      Complexe

Complex

Somme d’un réel et d’un imaginaire

*      Transfini

Transfinite

Au delà de l’infini

*      Surréel

Surreal

Nombres situés entre les infinis

Voir Ces types de nombres en détails

 

TYPE DE NOMBRES  - Classification

Entier naturel

0

1

2

3

*       Entiers positifs.

Relatif ou entier

-3

0

+3

*       Entiers avec signe: nombres positifs et nombres négatifs.

Rationnel

2

1/3

*       S'exprime par une fraction.

Rationnel: du vieux français " raison " qui voulait dire partage.

Décimal

2  ½

11 / 25

9, 3

cos ( / n)

 

*       Nombre rationnel qui s'exprime sous la forme n/10m avec n entier rationnel et m entier naturel.

Aussi

*       Nombre fractionnaire à développement fini

Exemple

1/2 = 0,5 = 0,500 …est décimal.

1/3 = 0,333... n'est pas un nombre décimal.

Irrationnel

2

7

 = 3, 14…

e = 2, 178…

j = 1, 618…

*       N'est pas solution d'une équation du premier degré à coefficients entiers

Ou

*       Il n'existe pas d'entiers rationnels tels que ax = b.

*       Les nombres irrationnels ont un développement décimal, comme fractionnaire, illimité!

2 = 1,4142136…

      = 1 + 1/ (2 + 1/ (2 + 1/ (2 + 1/...

Algébrique

2

 2

35

*       Racine d'un polynôme à coefficients entiers.

Exemples

x² - 2 = 0

x3 - 5 = 0

Transcendant

e

ln2

Par contre,

*       Il n'est pas possible d'associer une équation à coefficients entiers, ou rationnels, à tous les réels. Les récalcitrants sont les nombres

TRANSCENDANTS.

 

*       Les autres sont dits

ALGÉBRIQUES.

 

*       Les nombres transcendants sont infiniment plus nombreux que les nombres algébriques.

*       Démontrer qu'un nombre est transcendant est souvent très difficile.

Réel

2

2

 

*       Tous les nombres cités ci-dessus

 

Voir développement de ce tableau en Nombres dans leurs ensembles

 

 

 

 

Explications

 

*    On imagine bien les nombres entiers, ceux qui nous servent à compter.

*    Les nombres négatifs s'envisagent sans peine (de nos jours) en faisant allusion aux températures négatives et aussi à l'argent que l'on doit.

 

*    Les nombres rationnels sont ceux qui s'écrivent sous la forme d'une fraction. En calculant la fraction, c'est-à-dire en la transformant en un nombre à virgule (nombre décimal):

 

*    il n'y pas de décimale: 8/4 = 2;

*    il y a des décimales en nombre fini: 1/8 = 0,125; ou

*    il y a une infinité de décimales, mais elles sont répétées par paquets: 1/3 = 0,33333 …
                1/7 = 142857 142857 …

 

*    Parmi les autres nombres, on trouve:

 

*    ceux que l'on peut calculer en résolvant une équation à coefficients entiers (c'est le même principe que la fraction, mais en un peu plus compliqué).
Autrement-dit, on peut écrire une relation faisant émerger le nombre. C'est le cas de x² – 2 = 0 qui donne x = . Ce nombre, exprimable par une équation, mais pas par une fraction est dit "irrationnel".
Et ceux-ci accompagnés des autres (entiers, relatifs, rationnels) sont baptisés: algébrique. On les calcule en faisant de l'algèbre.

*     ceux qui ne se laissent même pas faire avec l'algèbre. aucune équation ne saurait les décrire. Parmi eux, il y le célèbre nombre . Ce sont les nombres transcendants.

 

*    Tous les nombres ainsi mentionnés ci-dessus, forme l'ensemble des nombres réels.
La marge jaune du tableau ci-dessus indique que tous ces ensembles de nombres s'emboitent, du plus petit au plus grand:

 

Illustration

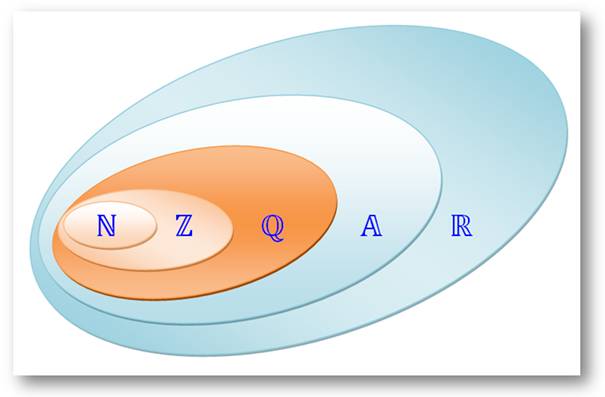
Naturel          Relatifs     Rationnels     Algébriques    Réels

Z vient de Zahl, nombre en allemand et Q de quotient d'une fraction.

La dernière "couronne"  (R – Z) représente les transcendants

 

Voir Diagramme complet

Voir Définition des nombres décimaux

 

*    Les mathématiciens ont de l'imagination. Ils ont pensé à forger d'autres nombres de toutes sortes. Par exemple, en associant deux nombres selon une relation particulière, ils ont inventé les nombres complexes.

 

 

 

 

 

 

Suite

*       Approche imaginée et raisonnement autour des types de nombres

*       Inventaire des ensembles de nombres

*       Types de nombres – Index

*       Découverte des nombres

*       Initiation aux calculs

*       Types de nombres Junior Diaporama

Voir

*       Calcul mental – Index

*       Carré magique débutant

*       Décimalisation

*       Ensemble - Glossaire

*       Nombre - Glossaire

*       Nombre et anglais

*       Rubriques débutants

Nombres

*       Liste des nombre de 0 à l'infini et de leurs propriétés

*       Un

*       Zéro

Cette Page

http://villemin.gerard.free.fr/Wwwgvmm/Type/NbDebut.htm